Основные теоретические сведения
1. При классическом определении вероятность события 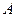 определяется соотношением определяется соотношением  . где . где  - число элементарных исходов испытания, благоприятствующих наступлению события - число элементарных исходов испытания, благоприятствующих наступлению события 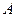 , а , а  - общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы единственно возможны и равновозможны. Относительная частота события - общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы единственно возможны и равновозможны. Относительная частота события 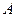 есть есть  , где , где  — число испытаний, в которых событие — число испытаний, в которых событие 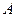 наступило, а наступило, а  — общее число произведенных испытаний. — общее число произведенных испытаний.
При статистическом определении в качестве вероятности события принимают его относительную частоту.
2. Схема испытаний Бернулли (повторение опытов). Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна 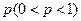 , событие наступит ровно , событие наступит ровно  раз (безразлично, в какой последовательности), есть раз (безразлично, в какой последовательности), есть
 , (1) , (1)
где  . .
Вероятность того, что событие наступит:
а) менее  раз: раз: 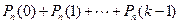 , ,
б) более  раз: раз:  , ,
в) не менее  раз: раз:  , ,
г) не более  раз: раз:  . .
3. Если число испытаний  велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются предельными теоремами Лапласа. велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются предельными теоремами Лапласа.
Локальная теорема Лапласа. Вероятность того, что в  независимых испытаниях, в каждом из которых вероятность появления события равна 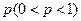 , событие наступит ровно  раз (безразлично, в какой последовательности), выражается приближенным равенством

где 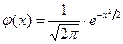 ; ; 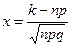 . .
Функция  - четная, т.е. - четная, т.е.  . При . При  можно считать, что можно считать, что  . .
Интегральная теорема Лапласа. Вероятность того, что в  независимых испытаниях, в каждом из которых вероятность появления события равна 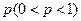 , событие наступит не менее  раз и не более  раз, выражается приближенным равенством
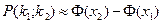 , ,
где  функция Лапласа; функция Лапласа;  ; ;  . При . При  полагают что, полагают что,  . Функция Лапласа - четная, т. е. . Функция Лапласа - четная, т. е.  ; ;  . .
4. Нормальным распределением называют распределение вероятностей случайной непрерывной величины X, плотность распределения которого имеет вид
 , ,
где  - математическое ожидание, а - математическое ожидание, а  - среднее квадратичное отклонение величины - среднее квадратичное отклонение величины  . .
Вероятность того, что  примет значение, принадлежащее интервалу примет значение, принадлежащее интервалу  , составляет , составляет
 ,
где  - функция Лапласа. - функция Лапласа.
Вероятность того, что абсолютная величина отклонения меньше положи тельного числа  , выражается равенством , выражается равенством
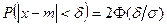 .
5. Если линия регрессии  на на  - прямая, то корреляцию называют линейной. Выборочное уравнение прямой линии регрессии - прямая, то корреляцию называют линейной. Выборочное уравнение прямой линии регрессии  на на  имеет вид имеет вид
 ,
где 
Если данные наблюдения над признаками  и и  заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам  , ,  , где , где  - ложный нуль вариант - ложный нуль вариант  (в качестве его выгодно принять варианту, расположенную при мерно и центре вариационного ряда и имеющую наибольшую частоту); (в качестве его выгодно принять варианту, расположенную при мерно и центре вариационного ряда и имеющую наибольшую частоту);  - шаг, т. е. разность между соседними вариантами - шаг, т. е. разность между соседними вариантами  . Величины . Величины  и и  относятся к варианте относятся к варианте  . В этом случае выборочный коэффициент корреляции . В этом случае выборочный коэффициент корреляции
 .
Величины  , ,  , ,  могут быть найдены либо методом произведений, либо непосредственно по формулам могут быть найдены либо методом произведений, либо непосредственно по формулам
 , ,  , ,  , ,  . .
Зная эти величины, можно определить входящие в уравнение регрессии значения по формулам
 ; ;  ; ;  ; ;  . .
Примеры решения типовых задач
Пример 1. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из 5 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут 2 женщины и 3 мужчины.
Решение. Число всех способов выбора 5 человек из 25 равно  , а число способов выбора двух женщин из 5 равно , а число способов выбора двух женщин из 5 равно  . Каждая такая двойка может сочетаться с каждой тройкой из 20 мужчин. Число таких троек равно . Каждая такая двойка может сочетаться с каждой тройкой из 20 мужчин. Число таких троек равно  . Искомая вероятность составляет . Искомая вероятность составляет
 . .
Пример 2. Слово «лотос», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают одну за другой три буквы. Какова вероятность того, что при этом появится слово «сто»?
Решение. Вероятность появления буквы «с» равна  вероятность появления вслед за ней буквы «т» равна вероятность появления вслед за ней буквы «т» равна  и, наконец, вероятность появления буквы «o» равна и, наконец, вероятность появления буквы «o» равна 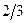 . Искомая вероятность . Искомая вероятность
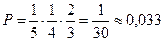 . .
Пример 3. Случайно встреченное лицо с вероятностью 0, 2 может оказаться брюнетом, с вероятностью 0, 3 — блондином, с вероятностью 0, 4 — шатеном и с вероятностью 0, 1— рыжим. Каковая вероятность того, что среди пяти случайно встреченных лиц; а) не менее четырех блондинов; б) два блондина и три шатена; в) хотя бы один рыжий?
Решение. а) Искомая вероятность есть [см. формулу (1)]
 . .
б) Искомая вероятность есть
 . .
в) Искомая вероятность есть
 . .
Пример 4. Игральную кость подбрасывают 500 раз. Какова вероятность того, что шестерка при этом выпадет 50 раз?
Решение. Здесь  , , 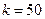 , , 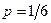 , ,  ; ; 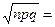
 ; ; 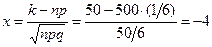 ; ;  . .
По формуле (2) находим искомую вероятность:
 . .
Пример 5. Пусть вероятность того, что покупателю необходимо купить обувь 41-го размера, равна 0, 2. Найти вероятность того, что из 400 покупателей не более 100 потребуют обувь этого размера.
Решение. По условию,  , ,  , ,  , , 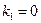 , ,  ; ;  ; ;  ; ;  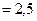 . Согласно формуле (3), искомая вероятность есть . Согласно формуле (3), искомая вероятность есть
 . .
Пример 6. Случайная непрерывная величина  распределена нормально. Известно, что распределена нормально. Известно, что  и и  . Найти . Найти  . .
Решение. По формуле (4) получим
 . .
Найдем  . Имеем . Имеем

откуда
 . .
Окончательно находим
 . .
Пример 7. Среднее квадратичное отклонение случайной величины, распределенной по нормальному закону, равно 2;  . Найти границы, и которых с вероятностью 0, 95 следует ожидать значения случайной величины. . Найти границы, и которых с вероятностью 0, 95 следует ожидать значения случайной величины.
Решение. По формуле (5) имеем
 . .
Найдем границы интервала:
 . .
Пример 8. Найти выборочное уравнение прямой линии 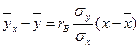 регрессии регрессии  и и  по данным корреляционной таблицы 1. по данным корреляционной таблицы 1.
Решение. Составим корреляционную таблицу (табл. 2) в условных вариантах, выбрав в качестве ложных нулей  и и  . .
Найдем  и и 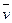
 ; ;
 . .
Таблица 1


|
|
|
|
|
|
| 
|

|
-7
-
-
-
|
-
-
-
| -
-
| -
-
| -
-
| -
-
-
-
|
 =100 =100
|
Таблица 2
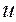

| -3
| -2
| -1
|
|
|
| 
| -2
-1

|
-
-
-
-
|
-
-
-
| -
-
| -
-
| -
-
| -
-
-
-
|
 =100 =100
| Найдем  к к  : :
 ; ;
 . .
Найдем  и и  : :
 ; ;
 . .
Найдем  , для чего составим расчетную таблицу. Суммируя числа последнего столбца табл. 3, получим , для чего составим расчетную таблицу. Суммируя числа последнего столбца табл. 3, получим  . Для контроля вычислений находим сумму чисел последней строки: . Для контроля вычислений находим сумму чисел последней строки:  . .
Указания к составлению табл. 3. Произведения частоты  на варианту на варианту  , т. е. , т. е.  , записывают в крайнем верхнем углу клетки, содержащей частоту. Складывают все числа, помещенные в правых верхних углах клеток данной строки, и их сумму помещают в клетку этой же строки «столбца , записывают в крайнем верхнем углу клетки, содержащей частоту. Складывают все числа, помещенные в правых верхних углах клеток данной строки, и их сумму помещают в клетку этой же строки «столбца  ». Умножают варианту ». Умножают варианту 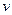 на на  и полученное произведение записывают в соответствующую клетку «столбца и полученное произведение записывают в соответствующую клетку «столбца  ». Сложив все числа «столбца ». Сложив все числа «столбца  », получают сумму », получают сумму  , которая равна искомой сумме , которая равна искомой сумме  . Для данной таблицы . Для данной таблицы  . Для контроля расчета аналогичные вычисления производят по столбцам: произведения . Для контроля расчета аналогичные вычисления производят по столбцам: произведения  записывают в левый нижний угол клетки, содержащей частоту; все числа, помещенные в левый нижних углах одного столбца, складывают и их сумму помещают в «строку записывают в левый нижний угол клетки, содержащей частоту; все числа, помещенные в левый нижних углах одного столбца, складывают и их сумму помещают в «строку  ». Умножают каждую варианту ». Умножают каждую варианту  на на  и результат записывают в клетках последней строки. Сложив все числа последней строки, получают сумму и результат записывают в клетках последней строки. Сложив все числа последней строки, получают сумму  , которая также равна искомой сумме , которая также равна искомой сумме  (в данном случае 72). По формуле (7) найдем искомый выборочный коэффициент корреляции: (в данном случае 72). По формуле (7) найдем искомый выборочный коэффициент корреляции:
 . .
Далее находим  и и  , ,  и и 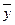 , ,  и и  : :
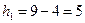 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 . .
Подставив найденные величины в формулу (6), получим
 , ,
Или
 . .
Контрольная работа №8
Задача №40.
| №
| Условие
| |
| Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0, 75; для второго стрелка – 0, 8; для третьего – 0, 9. Найти вероятность того, что: 1) все три стрелка попадут в цель; 2) все три промахнутся; 3) только один стрелок попадет в цель; 4) хотя бы один стрелок попадет в цель.
| |
| В первом ящике 6 белых и 4 черных шара, во втором – 7 белых и 3 черных из каждого ящика вынимают по одному шару. Чему равна вероятность того, что вынутые шары разного цвета?
| |
| На двух станках производятся одинаковые детали. Вероятность того, что деталь стандартная, для первого станка равна 0, 8; для второго – 0, 9. производительность второго станка втрое больше, чем у первого. Найти вероятность того, что взятая наудачу деталь окажется стандартной.
| |
| На пяти карточках написано по одной цифре из набора: 1, 2, 3, 4, 5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой?
| |
| Из партии, в которой 20 деталей без дефектов и 5 с дефектами, берут наудачу 3 детали. Чему равна вероятность того, что: 1) все три детали без дефектов; 2) по крайней мере, одна деталь без дефектов?
| |
| Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово «ракета»?
| |
| Ящик содержит 10 деталей, среди которых 3 стандартных. Найти вероятность того, что из наудачу отобранных 5 деталей окажется не более одной стандартной.
| |
| Брошены два одинаковых игральных кубика. Найти вероятность того, что цифра 6 появится хотя бы на одной грани.
| |
| Для поражения цели достаточно попадания хотя бы одного снаряда. Произведено два залпа из двух орудий. Найти вероятность поражения цели, если вероятность попадания в цель при одном выстреле из первого орудия равна 0, 3; а из второго – 0, 4.
| |
| В урне лежат 12 белых и 8 красных шаров. Вынули 8 шаров. Какова вероятность того, что: 1) три из них – красные; 2)красных шаров вынуто не более трех.
| |
| В урне 4 белых и 6 чёрных шаров. Из неё вынимают сразу 2 шара. Найти вероятность того, что оба шара будут белыми.
| |
| В урне 4 белых и 8 чёрных шаров. Из неё вынимаются один за другим два шара. Найти вероятность того, что они будут разных цветов.
| |
| Производится три независимых выстрела по мишени; вероятность попадания при первом, втором и третьем выстрелах равны соответственно:  1) Найти вероятность того, что будет ровно два попадания.
2) Найти вероятность хотя бы одного попадания.
1) Найти вероятность того, что будет ровно два попадания.
2) Найти вероятность хотя бы одного попадания.
| |
| Из колоды карт, содержащей 32 листа, вынимаются наугад 4 карты. Найти вероятность того, что среди них будет хотя бы один туз.
| |
| В шкафу находятся 9 однотипных приборов. В начале опыта они все новые (ни разу не бывшие в эксплуатации). Для временной эксплуатации берут наугад три прибора; после эксплуатации и возвращают в шкаф. На вид прибор, бывший в эксплуатации, ничем не отличается от нового. Такого рода операция проводится три раза. Найти вероятность того, что в результате трехкратного выбора и эксплуатации в шкафу останется хотя бы один новый прибор.
| |
| Завод изготавливает изделия, каждое из которых с вероятностью 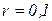 (независимо от других) является дефектным. Для контроля из продукции завода выбирается наугад (независимо от других) является дефектным. Для контроля из продукции завода выбирается наугад  изделий. При осмотре дефект, если он существует, обнаруживается с вероятностью изделий. При осмотре дефект, если он существует, обнаруживается с вероятностью  . Найти вероятность следующих событий: . Найти вероятность следующих событий:
 Ни в одном из изделий не обнаружено дефектов Ни в одном из изделий не обнаружено дефектов 
 Среди 10 изделий ровно в двух обнаружен дефект Среди 10 изделий ровно в двух обнаружен дефект 
 Среди 10 изделий не менее чем в двух обнаружен дефект Среди 10 изделий не менее чем в двух обнаружен дефект 
| |
| По каналу связи передаются 5 сообщений. Каждое из них (независимо от других) с вероятностью 0, 1 искажается. Найти вероятности следующих событий:
 Все сообщения будут переданы без искажения Все сообщения будут переданы без искажения 
 Все сообщения будут искажены Все сообщения будут искажены 
 Не менее двух сообщений будет искажено Не менее двух сообщений будет искажено 
| |
| Прибор, обладающий надежностью (вероятностью безотказной работы за время  часов) равный 0, 9 представляется недостаточно надежным. Для повышения надежности он дублируется еще одним точно таким же работающим прибором. Если первый прибор за время часов) равный 0, 9 представляется недостаточно надежным. Для повышения надежности он дублируется еще одним точно таким же работающим прибором. Если первый прибор за время  часов отказал, происходит автоматическое (и безотказное) переключение на дублирующий. Приборы отказывают независимо друг от друга. Найти вероятность того, что система из двух приборов проработает безотказно время часов отказал, происходит автоматическое (и безотказное) переключение на дублирующий. Приборы отказывают независимо друг от друга. Найти вероятность того, что система из двух приборов проработает безотказно время  часов. часов.
| |
| Сколько нужно поставить дублирующих приборов с той же надежностью 0, 8, что и основной, чтобы надежность системы приборов была не ниже заданной величины 0, 98?
| |
| Прибор состоит из 4 блоков, каждый из которых (независимо от других) за время  часов эксплуатации прибора может отказать (выйти из строя). Надежность (вероятность безотказной работы за время часов эксплуатации прибора может отказать (выйти из строя). Надежность (вероятность безотказной работы за время  часов) каждого блока равна 0, 8. Безотказная работа всех без исключения блоков необходима для безотказной работы прибора в целом. Найти вероятность того, что в течении времени часов) каждого блока равна 0, 8. Безотказная работа всех без исключения блоков необходима для безотказной работы прибора в целом. Найти вероятность того, что в течении времени  часов прибор будет работать безотказно. часов прибор будет работать безотказно.
|
Задача №41
| №
| Условие
| |
| Вероятность появления события А при одном испытании равна 0, 1. Найти вероятность того, что при трех независимых испытаниях оно появится: 1) не менее двух раз; 2) хотя бы один раз.
| |
| Игральную кость подбрасывают три раза. Найти вероятность того, что дважды появится число очков кратное трем.
| |
| Событие В появится в случае, если событие А появится не менее четырех раз. Найти вероятность того, что наступит событие В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0, 5.
| |
| Случайно встреченное лицо может оказаться, с вероятностью р=0, 2, брюнетом; с р=0, 3 – блондином; с р=0, 4 – шатеном и с р=0, 1 – рыжим. Какова вероятность того, что среди трех случайно встреченных лиц: 1) не менее 2-х брюнетов; 2) один блондин и два шатена; 3) хотя бы один рыжий.
| |
| Вероятность хотя бы одного попадания при двух выстрелах равна 0, 99. Найти вероятность трех попаданий при четырех выстрелах.
| |
| В квартире четыре электролампочки. Для каждой лампочки вероятность того, что она останется исправной в течение года, равна  ; Какова вероятность того, что в течении года придется заменить не менее половины лампочек. ; Какова вероятность того, что в течении года придется заменить не менее половины лампочек.
| |
| В ящике имеется по одинаковому числу деталей, изготовленных заводами №1 и №2. Найти вероятность того, что среди пяти наудачу отобранных деталей, изготовленных заводом №1: 1) две детали; 2) менее двух деталей; 3) более двух деталей.
| |
| Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0, 2. Найти вероятность того, что в течение гарантийного срока из трех телевизоров: 1) не более одного потребует ремонта; 2) хотя бы один не потребует ремонта.
| |
| В ящике лежат несколько тысяч одинаковых предохранителей. Половина из них изготовлена 1-м заводом, остальные 2-м заводом. Наудачу вынули пять предохранителей. Чему равна вероятность того, что 1-м заводом из них изготовлены: 1) два предохранителя; 2) менее двух предохранителей; 3) более 2-х предохранителей.
| |
| ОТК проверяет изделия на стандартность. Вероятность того, что изделие нестандартно, равно 0, 1. Найти вероятность того, что: 1) из трех проверенных изделий только одно нестандартное; 2) нестандартным будет только третье по порядку проверенное изделие.
| |
| 32 буквы разрезной азбуки смешали между собой. Наугад вынимается одна карточка, стоящая на ней буква записывается, карточка возвращается обратно и смешивается с другими. Такой опыт проводится 25 раз. Событие А состоит в том, что после 25 вынимании мы запишем первую строчку «Евгения Онегина»: «Мой дядя самых честных правил …» Найти вероятность данного события.
| |
| События может передаваться по одному из каналов связи находящихся в различных состояниях: из них  каналов находятся в отличном состоянии, каналов находятся в отличном состоянии,  - в хорошем, - в хорошем,  в посредственном и в посредственном и  в плохом состоянии (где: n= в плохом состоянии (где: n= 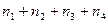 =12+40+56+24=132). Вероятность правильной передачи сообщения для разного вида каналов равна соответственно: =12+40+56+24=132). Вероятность правильной передачи сообщения для разного вида каналов равна соответственно:  ; ; 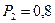 ; ;  ; ;  . Для повышения его достоверности сообщение передается по два раза по одному и тому же каналу, который выбирается наугад. Найти вероятность того, что хотя бы один раз оно будет передано правильно. . Для повышения его достоверности сообщение передается по два раза по одному и тому же каналу, который выбирается наугад. Найти вероятность того, что хотя бы один раз оно будет передано правильно.
| |
| При одном цикле обзора радиолокационной станции (РЛС), объект-корабль – обнаруживается с вероятностью 0, 7; при следующем цикле обзора он теряется с вероятностью 0, 4. Если при следующем цикле обзора объект-корабль не потерян, то слежение за объектом продолжается, сколько потребуется циклов обзора для того, чтобы с вероятностью не менее 0, 95 установить устойчивое слежение за объектом-кораблем?
| |
| Производится 100 независимых опытов, в каждом из которых событие А появляется с вероятностью 0, 65. Сколько нужно сделать опытов для того, чтобы с вероятностью  гарантировать хотя бы одно появление события А? гарантировать хотя бы одно появление события А?
| |
| Прибор состоит из элементов, надежность каждого из которых равна 0, 9. Выход из строя любого каждого из элементов равносилен выходу из строя прибора в целом. Не больше какого числа n элементов должно быть в приборе, для того, чтобы надежность прибора не стала меньше 0, 94.
| |
| Имеются три одинаковые на вид урны: в первой – 12 белых шаров и 18 черных шаров; во второй – 24 белых и 4 черных; в третьей – 6 белых шаров. Некто подходит наугад к одной из урн и вынимает из нее один шар. Найти вероятность того, что этот шар будет белым.
| |
| Прибор может работать в трех режимах: 1) нормальном; 2) форсированном; 3) недогруженном. Нормальный режим наблюдается в 60% случаев работы прибора, форсированном – 30% и недогруженном – 10%. Надежность прибора (вероятность безотказной работы в течение данного времени t=500 часов) для нормального режима равна 0, 8; для форсированного 0, 5; для недогруженного 0, 9. Найти полную (с учетом случайности условий) надежность прибора.
| |
| Имеются две партии однородных деталей. Первая – состоит из N=200 изделий, среди которых n=24 дефектных; вторая – состоит из M=300 изделий, среди которых 34 дефектных. Из первой партии берут случайным образом 15 изделий, из второй – 25 изделий и их смешивают между собой. Из полученной партии изделий берут наугад одно. Какова вероятность того, что взятое наугад изделие будет дефектным?
| |
| Прибор состоит из двух дублирующих друг друга узлов и может работать в одном из двух режимов: нормальном и неблагоприятном. Нормальный режим наблюдается в 85% случаев эксплуатации прибора, а неблагоприятный – в 15%. Надежность (вероятность безотказной работы) каждого из узлов в нормальном режиме равна 0, 9; а в неблагоприятном 0, 6. При выходе из строя (отказе) узла происходит автоматическое безотказное переключение на дублера. Найти полную вероятность безотказной работы прибора.
| |
| Завод производит изделия, каждое из которых независимо от других с вероятностью 0, 1 имеет дефект. В цехе имеется три контролера: изделие осматривается только одним из них (с одинаковой вероятностью 1-м, 2-м, или 3-м). Вероятность обнаружения дефекта, если он имеется, для 1-го, 2-го и 3-го контролеров равна соответственно 0, 9; 0, 8; 0, 7. При обнаружении дефекта изделие бракуется. Если изделие не было забраковано в цехе, то оно отправляется на ОТК завода, где дефект, если он имеется, обнаруживается с вероятностью 0, 55. Изделие, дефект которого обнаружен, бракуется. Найти вероятность того, что изделие будет забраковано.
|
Задача №42
Популярное:
|


 независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна 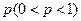 , событие наступит ровно
, событие наступит ровно  раз (безразлично, в какой последовательности), выражается приближенным равенством
раз (безразлично, в какой последовательности), выражается приближенным равенством

 независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна 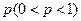 , событие наступит не менее
, событие наступит не менее  раз и не более
раз и не более  раз, выражается приближенным равенством
раз, выражается приближенным равенством  ,
,
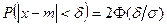 .
.
 ,
,
 .
.