Момент силы относительно полюса (центра, точки)
Момент силы относительно полюса характеризует меру вращательной способности силы, приложенной к телу, имеющему неподвижную точку. Так как он должен указывать направление оси возможного поворота, то это должен быть вектор.
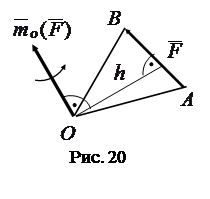 Определение: Моментом силы относительно полюса называется вектор (рис. 20), приложенный в полюсе, направленный перпендикулярно плоскости, проходящей через полюс и силу в ту сторону, откуда видно, что сила стремится вращать тело вокруг полюса против часовой стрелки, и равный по величине произведению величины силы на плечо. Плечом называется длина перпендикуляра, опущенного из полюса на линию действия силы.
Определение: Моментом силы относительно полюса называется вектор (рис. 20), приложенный в полюсе, направленный перпендикулярно плоскости, проходящей через полюс и силу в ту сторону, откуда видно, что сила стремится вращать тело вокруг полюса против часовой стрелки, и равный по величине произведению величины силы на плечо. Плечом называется длина перпендикуляра, опущенного из полюса на линию действия силы.
Обозначение:  . Читается так: момент силы
. Читается так: момент силы  относительно полюса
относительно полюса  . Величина момента
. Величина момента  . Так как плечо
. Так как плечо  можно рассматривать как высоту треугольника
можно рассматривать как высоту треугольника  , о можно сказать, что величина момента силы относительно полюса равна удвоенной площади треугольника
, о можно сказать, что величина момента силы относительно полюса равна удвоенной площади треугольника 
 .
.
Заметим, что эта " площадь" будет измеряться в ньютоно-метрах, так как основание треугольника–сила, а высота–длина.
Основные свойства момента силы относительно полюса
1. Момент силы относительно полюса не изменяется, если силу переносить вдоль ее линии действия.
2. Если линия действия силы проходит через полюс, то момент силы относительно полюса равен нулю.
3. Сумма моментов двух прямопротивоположных сил относительно одного и того же полюса равна нулю.
Эти свойства легко проверяются.
4.3. Момент силы относительно полюса как векторное произведение
Определим положение точки приложения силы  вектором
вектором  , который называется радиус-вектором точки приложения силы (рис. 21).
, который называется радиус-вектором точки приложения силы (рис. 21).
Тогда справедлива теорема.
Теорема. Момент силы относительно полюса равен векторному произведению радиус-вектора точки приложения силы на вектор силы, то есть
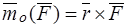 .
.
Доказательство:
Такое представление момента силы относительно полюса легко проверяется. Для этого покажем, что векторы, стоящие в правой и левой частях этого равенства, равны по величине и одинаково направлены. В самом деле, модуль векторного произведения равен
 ,
,
где  —плечо силы. По определению вектор
—плечо силы. По определению вектор  направлен перпендикулярно плоскости, содержащей векторы
направлен перпендикулярно плоскости, содержащей векторы 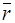 и
и  (плоскости
(плоскости  ), в ту сторону, откуда кратчайший поворот вектора
), в ту сторону, откуда кратчайший поворот вектора 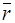 к направлению вектора
к направлению вектора  представляется происходящим против часовой стрелки, то есть так же, как вектор
представляется происходящим против часовой стрелки, то есть так же, как вектор  . Следовательно, векторы
. Следовательно, векторы  и
и  совпадают и по величине и по направлению.
совпадают и по величине и по направлению.
Связь между моментами силы относительно полюса и оси
Теорема. Проекция момента силы  относительно полюса
относительно полюса  на ось
на ось 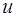 , проходящую через этот полюс, равна моменту силы
, проходящую через этот полюс, равна моменту силы  относительно оси
относительно оси 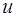 :
:
 .
.
Доказательство:
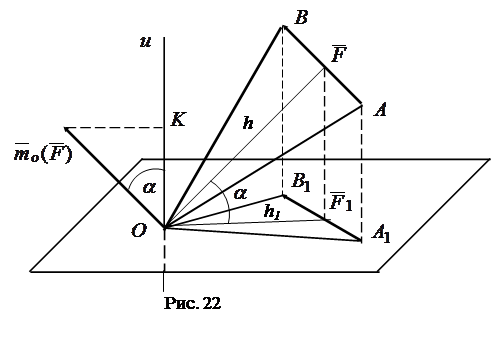 Для доказательства вычислим левую и правую части предполагаемого равенства и убедимся, что результаты вычислений совпадают (рис. 22).
Для доказательства вычислим левую и правую части предполагаемого равенства и убедимся, что результаты вычислений совпадают (рис. 22).
Момент силы  относительно полюса
относительно полюса  перпендикулярен плоскости треугольника
перпендикулярен плоскости треугольника  и по величине
и по величине  . Обозначим угол между
. Обозначим угол между  и осью
и осью 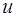 через
через 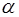 . Тогда проекция
. Тогда проекция  на ось
на ось 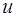 :
:

Проведем через полюс  плоскость, перпендикулярную оси и вічислим момент силі
плоскость, перпендикулярную оси и вічислим момент силі  относительно оси
относительно оси 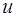 :
:

(рассматривается случай, когда  стремится повернуть плоскость вокруг оси против хода часовой стрелки).
стремится повернуть плоскость вокруг оси против хода часовой стрелки).
Воспользуемся простым положением элементарной геометрии: площадь проекции плоской фигуры (  ) на некоторую плоскость (
) на некоторую плоскость ( 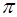 ) равна площади проектируемой фигуры (
) равна площади проектируемой фигуры ( 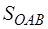 ), умноженной на косинус угла между плоскостью проекции и плоскостью проектируемой фигуры. Угол между двумя плоскостями – это угол между перпендикулярами к этим плоскостям в их общей точке, то есть угол
), умноженной на косинус угла между плоскостью проекции и плоскостью проектируемой фигуры. Угол между двумя плоскостями – это угол между перпендикулярами к этим плоскостям в их общей точке, то есть угол 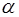 . Тогда
. Тогда 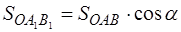 . Следовательно
. Следовательно
 .
.
Главный момент системы сил
Определение. Главным моментом системы сил относительно полюса  называется геометрическая сумма моментов всех сил системы относительно этого полюса.
называется геометрическая сумма моментов всех сил системы относительно этого полюса.
Обозначение:  , или
, или 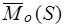 . Если задана система сил
. Если задана система сил 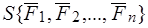 , то
, то
 .
.
Определение. Главным моментом системы сил относительно оси 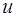 называется алгебраическая сумма моментов всех сил системы относительно этой оси.
называется алгебраическая сумма моментов всех сил системы относительно этой оси.
Обозначение:  , или
, или 
 .
.
Теорема. Проекция главного момента системы сил относительно полюса  на ось
на ось 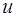 , проходящую через этот полюс, равна главному моменту сил системы относительно этой оси, то есть
, проходящую через этот полюс, равна главному моменту сил системы относительно этой оси, то есть
 .
.
Доказательство:
Главный момент системы сил 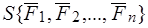 относительно полюса
относительно полюса 
 .
.
Спроектируем это векторное равенство на ось 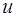 , проходящую через полюс
, проходящую через полюс  :
:
 .
.
На основании теоремы о связи между моментом силы относительно полюса и моментом силы относительно оси

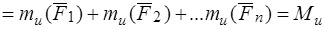 .
.
Следовательно  .
.
 4.6. Зависимость между главными моментами системы сил относительно двух полюсов
4.6. Зависимость между главными моментами системы сил относительно двух полюсов
Дана система сил  и два полюса: старый
и два полюса: старый  и новый
и новый  (рис. 23).
(рис. 23).
Главный момент системы сил относительно старого полюса:

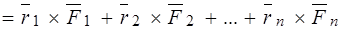 .
.
Главный момент относительно нового полюса:
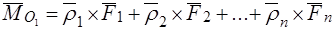 .
.
Здесь  и
и 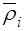 (
( 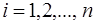 )–радиус-векторы точки приложения силы
)–радиус-векторы точки приложения силы  относительно старого и нового полюсов соответственно.
относительно старого и нового полюсов соответственно.
Из рисунка видно, что:

 .
.
Тогда

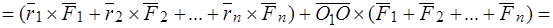
 ,
,
где 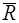 –главный вектор. Пришли к теореме о зависимости между главными моментами системы сил относительно двух полюсов.
–главный вектор. Пришли к теореме о зависимости между главными моментами системы сил относительно двух полюсов.
Теорема. Главный момент системы сил относительно нового полюса равен сумме главного момента системы сил относительно старого полюса и момента главного вектора, приложенного к старому полюсу относительно нового –полюса, то есть
 .
.
Следствие 1. Если главный вектор системы сил равен нулю, то ее главный момент не зависит от выбора полюса, то есть, если 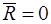 , то
, то  .
.
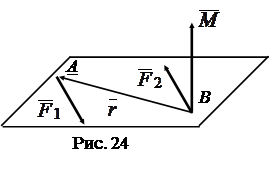 Следствие 2. Главный момент пары сил не зависит от выбора полюса и отличен от нуля.
Следствие 2. Главный момент пары сил не зависит от выбора полюса и отличен от нуля.
Дана пара сил {  } (рис. 24).
} (рис. 24).  ,
,  . Так как главный вектор
. Так как главный вектор  . То главный момент пары не зависит от выбора полюса:
. То главный момент пары не зависит от выбора полюса:
 .
.
Линия действия силы  проходит через полюс
проходит через полюс  , то есть
, то есть 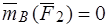 , и:
, и:
 .
.
Популярное:
- A. Оценка будущей стоимости денежного потока с позиции текущего момента времени
- F. Оценка будущей стоимости денежного потока с позиции текущего момента времени
- VI. ЧЕЛОВЕК – СОКРОВИЩНИЦА ДУХОВНОЙ СИЛЫ
- А теперь несколько высказываний различных педагогов относительно артикуляции и дикции.
- Альберт Эйнштейн (1879–1955), физик, создатель теории относительности.
- Анализ информации, получаемой от САРП. Режимы истинного и относительного движения, их достоинства и недостатки. Проигрывание маневра. Возможная опасность чрезмерного доверия САРП.
- Б-16.1..Модель двигательного режима в режимных моментах детского сада
- Б-6.1.Организация и проведение режимных моментов(умывание , одевание, питание ,сон)
- В покаянии есть много полезных моментов
- В условиях, связанных с применением физической силы, специальных средств, огнестрельного оружия
- В чем настоящий секрет силы?
- В это время князь Владимир у Волок-Ламского и великий князь Дмитрий в Костроме собрали значительные силы. Один из татарских отрядов, двигавшийся к Волок-Ламскому, был внезапно атакован и разбит.

