
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Центр системы параллельных сил
Система параллельных сил в общем случае приводится к силе и паре, причем векторы силы и пары перпендикулярны. Тогда, если
Рассмотрим систему параллельных сил 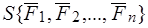 , приложенных соответственно в точках , приложенных соответственно в точках 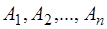 твердого тела (рис. 46). твердого тела (рис. 46).
Определение. Центром системы параллельных сил называется точка приложения равнодействующей системы параллельных сил, которая остается неизменной при любых поворотах всех сил системы вокруг их точек приложения на один и тот же угол. Центр параллельных сил существует, если главный вектор системы сил не равен нулю Пусть
или Тогда Преобразуем полученное выражение:
Выражение в круглых скобках представляет собой некоторый вектор, который обозначим
Но
откуда получаем выражение для радиус-вектора центра параллельных сил Проектируя полученное равенство на оси координат, получим выражения для координат центра параллельных сил где
Центр тяжести твердого тела Силы притяжения отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Равнодействующая этих параллельных сил, равная их сумме, есть вес тела. Определение. Центром тяжести твердого тела называется центр параллельных сил тяжести частиц, слагающих тело. Иными словами, центр тяжести – это такая точка приложения равнодействующей сил тяжести частиц тела, которая остаётся неизменной при любых поворотах тела. Таким образом, для определения положения центра тяжести можно использовать формулы для координат центра параллельных сил.
Обозначим силы веса отдельных частиц тела  , вес тела , вес тела  , координаты его центра тяжести , координаты его центра тяжести  , а координаты любой частицы твердого тела , а координаты любой частицы твердого тела  (рис. 47). (рис. 47).
Тогда формулы для определения координат центра тяжести принимают вид:
Определим положение центра тяжести однородных тел.
1. Центр тяжести объема Вес однородного тела определяется по формуле
Однородное тело, имеющее форму тонкой пластинки, можно рассматривать как плоскую фигуру. Положение центра тяжести плоской фигуры определяется двумя координатами
3. Центр тяжести линии Пусть Тогда:
Статические моменты Статическими моментами называются выражения, стоящие в числителях формул для радиус- вектора центра тяжести. Например, из формулы
получаем статический момент относительно полюса:
Статическим моментом плоской фигуры относительно оси Статический момент площади плоской фигуры относительно оси измеряется в кубических метрах – Если известны статические моменты площади плоской фигуры относительно координатных осей, то координаты ее центра тяжести можно определить по формулам
Очевидно, что если статический момент плоской фигуры относительно некоторой оси равен нулю, то центр тяжести этой фигуры лежит на этой оси.
Популярное:
|
Последнее изменение этой страницы: 2016-05-30; Просмотров: 2001; Нарушение авторского права страницы