
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Теорема о равновесии тела под действием сходящейся системы сил(векторные условия равновесия)Стр 1 из 6Следующая ⇒
ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ Сила и система сил Сила – векторная величина, являющаяся мерой механического действия одного материального тела на другое. Всякая сила характеризуется величиной, направлением и точкой приложения. Сила – приложенный вектор. Линия действия силы – прямая, проходящая через точку приложения силы и вдоль которой расположена сила. Системой сил называется совокупность сил, приложенных к твердому телу. Обозначение: Две параллельные силы, равные по величине, направленные в противоположные стороны, называются парой сил, или просто парой (рис. 1).
Две силы, равные по величине, направленные в противоположные стороны и имеющие общую линию действия, называются прямо противоположными
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся системой сил(рис. 3). Точка Система сил, линии действия которых параллельны между собой, называется системой параллельных сил. Кроме сходящихся и параллельных систем сил различают произвольные системы сил– это системы сил, линии действия которыхрасположены как угодно в пространстве (пространственная система сил) или на плоскости (плоская система сил). Всякой силе ставится в соответствие свободный вектор – вектор силы. Вектором силы называется свободный вектор, параллельный силе, направленный в ту же сторону и имеющий длину, равную длине силы. Главным вектором системы сил называется свободный вектор, равный геометрической сумме векторов сил, составляющих систему. Обозначение: Если задана система сил
Строится главный вектор как геометрическая сумма векторов. Например, на тело действует система сил  (рис. 4). (рис. 4).
Из произвольной точки
Аксиомы статики Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами статики. Аксиомы статики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой.
Аксиома 1. Под действием двух сил твердое тело находится в равновесии тогда и только тогда, когда эти силы прямо противоположны, то есть равны по величине, направлены в противоположные стороны и имеют общую линию действия (рис. 5). Аксиома 2. Равновесие твердого тела не нарушится, если к силам, действующим на тело, присоединить, либо из числа сил, действующих на тело, изъять, если таковые имеются, две прямо противоположные силы. Следствие 1. Равновесие твердого тела не нарушится, если любую из сил, приложенных к телу, перенести вдоль ее линии действия.
Действительно, пусть сила  приложена в точке приложена в точке 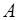 (рис. 6а). (рис. 6а).
Приложим в произвольной точке
Аксиома 3. Равновесие твердого тела нарушится, если две силы, приложенные к одной его точке, заменить одной силой, приложенной в той же точке и равной их геометрической сумме (по правилу параллелограмма), либо одну силу заменить двумя ее составляющими (по тому же правилу).
Следствие 2. Равновесие твердого тела не нарушится, если действующую на него систему сходящихся сил заменить одной силой, которая приложена в точке схода и равна главному вектору этой системы сил. Согласно следствию 1, не нарушая равновесие тела, переносим силы Следствие 3. Под действием одной силы тело не может находиться в состоянии равновесия. Для доказательства разложим эту силу на две составляющие по правилу параллелограмма. Эти составляющие не прямо противоположны, следовательно, на основании аксиомы 1 тело не будет находиться в состоянии равновесия.
Аксиома 4 (третий закон Ньютона) Источником каждой силы является материальное тело, причем два тела действуют друг на друга с прямо противоположными силами. Следует помнить, что силы действия Аксиома 5 (принцип отвердевания). Состояние равновесия изменяемого(деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим(абсолютно твердым).
СВЯЗИ И ИХ РЕАКЦИИ Различают тела свободные и несвободные. Твердое тело называется свободным, если из данного положения его можно перевести в любое смежное. Несвободным телом называется тело, перемещение которого в каком либо одном или нескольких направлениях ограничено. Тела (устройства, приспособления), которые препятствуют каким либо перемещениям данного тела, называются связями, наложенными на тело. Связи, наложенные на тело, являются источником сил, действующих на это тело и называемых реакциями связей. О с н о в н ы е т и п ы с в я з е й
1. Идеально гладкая (без трения) поверхность Поверхность называется идеально гладкой, если она не оказывает сопротивления соприкасающемуся с ней телу при перемещении тела по поверхности. Такая поверхность не дает телу перемещаться только по направлению нормали к этой поверхности. Поэтому реакция
Таким образом, при определении реакции идеально гладкой поверхности необходимо определить одну неизвестную величину реакции, так как направление этой реакции известно. Когда говорят, что тело свободно опирается на поверхность, предполагается, что поверхность идеально гладкая.
2. Гибкая нерастяжимая нить (трос, цепь, канат)
Реакция гибкой, нерастяжимой и невесомой нити направлена вдоль нити, внутрь нити (рис. 11) Нить может работать только на растяжение.
3. Связи с неподвижной осью вращения (цилиндрический шарнир, подшипник)
Неизвестные вектор
4. Связь с неподвижным центром вращения (сферический шарнир)
Сферическим шарниром называется устройство, изображенное на рис 13а, которое делает неподвижной точку  рассматриваемого тела. рассматриваемого тела.
Предполагается, что сферические поверхности контакта идеально гладкие. Тогда реакция сферического шарнира имеет направление нормали к его поверхности. Единственное, что известно относительно реакции – это то, что она проходит через центр шарнира
5. Опорный стержень
Реакция такого идеального стержня направлена вдоль оси стержня, в чем не трудно убедиться. Действительно, если силы приложены только к концам стержня, то он находится в равновесии под действием двух сил, а по аксиоме 1 это возможно, если эти силы пряморотивоположны—направлены по прямой, соединяющей концы стержня. Если реакции направлены наружу (рис. 14а) – стержень сжат, если внутрь (рис. 14б) – растянут. Так как растягивающему усилию приписывают знак плюс, то направляя реакцию вовнутрь, мы получаем величину усилия со знаком плюс. На рис 14в изображен растянутый стержень с криволинейной осью.
СИСТЕМА СХОДЯЩИХСЯ СИЛ МОМЕНТ СИЛЫ Главный момент системы сил Определение. Главным моментом системы сил относительно полюса Обозначение:
Определение. Главным моментом системы сил относительно оси Обозначение:
Теорема. Проекция главного момента системы сил относительно полюса Доказательство: Главный момент системы сил
Спроектируем это векторное равенство на ось
На основании теоремы о связи между моментом силы относительно полюса и моментом силы относительно оси
Следовательно
Дана система сил Главный момент системы сил относительно старого полюса:
Главный момент относительно нового полюса:
Здесь Из рисунка видно, что:
Тогда
где Теорема. Главный момент системы сил относительно нового полюса равен сумме главного момента системы сил относительно старого полюса и момента главного вектора, приложенного к старому полюсу относительно нового –полюса, то есть
Следствие 1. Если главный вектор системы сил равен нулю, то ее главный момент не зависит от выбора полюса, то есть, если
Дана пара сил {
Линия действия силы
Основная лемма статики Леммой называют теорему, необходимую только для доказательства другой теоремы. Лемма. Любая система сил эквивалентна системе из двух сил, то есть любая система сил с помощью элементарных операций может быть приведена к двум силам. Доказательство.
Предварительно докажем лемму для трех сил  , ,  , ,  . .
Проведем две плоскости (рис. 26); одну через силу Эти плоскости, имея общую точку
Заменяем силы  и и 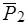 , приложенные в точке , приложенные в точке  , их геометрической суммой , их геометрической суммой  , приложенной в той же точке: , приложенной в той же точке:  , а силы , а силы  , приложенные в точке , приложенные в точке  – силой – силой  , приложенной так же в точке , приложенной так же в точке  . В результате применения только элементарных операций система сил { . В результате применения только элементарных операций система сил {  } приведена к двум силам { } приведена к двум силам { 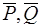 }. Итак, заданная система сил { }. Итак, заданная система сил {  } эквивалентна двум силам { } эквивалентна двум силам { 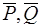 }: }:
{ что и требовалось доказать. Если задана система, состоящая из { { { …… … { ТЕОРИЯ ПАР СИЛ Момент пары сил
Плоскость, в которой лежит пара сил, называется плоскостью пары. Как уже отмечалось, главный момент пары не зависит выбора полюса и отличен от нуля.
Главный момент пары, не зависящий от выбора полюса, называется моментом пары. Обозначение: Момент пары – это свободный вектор, перпендикулярный плоскости пары, направленный в ту сторону, откуда видно, что пара стремится вращать тело против часовой стрелки, и равный по величине произведению одной из сил пары на кратчайшее расстояние между линиями действия сил пары (плечо пары).
Центр тяжести твердого тела Силы притяжения отдельных частиц тела к Земле направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Равнодействующая этих параллельных сил, равная их сумме, есть вес тела. Определение. Центром тяжести твердого тела называется центр параллельных сил тяжести частиц, слагающих тело. Иными словами, центр тяжести – это такая точка приложения равнодействующей сил тяжести частиц тела, которая остаётся неизменной при любых поворотах тела. Таким образом, для определения положения центра тяжести можно использовать формулы для координат центра параллельных сил.
Обозначим силы веса отдельных частиц тела  , вес тела , вес тела  , координаты его центра тяжести , координаты его центра тяжести  , а координаты любой частицы твердого тела , а координаты любой частицы твердого тела  (рис. 47). (рис. 47).
Тогда формулы для определения координат центра тяжести принимают вид:
Определим положение центра тяжести однородных тел.
1. Центр тяжести объема Вес однородного тела определяется по формуле
Однородное тело, имеющее форму тонкой пластинки, можно рассматривать как плоскую фигуру. Положение центра тяжести плоской фигуры определяется двумя координатами
3. Центр тяжести линии Пусть Тогда:
Статические моменты Статическими моментами называются выражения, стоящие в числителях формул для радиус- вектора центра тяжести. Например, из формулы
получаем статический момент относительно полюса:
Статическим моментом плоской фигуры относительно оси Статический момент площади плоской фигуры относительно оси измеряется в кубических метрах – Если известны статические моменты площади плоской фигуры относительно координатных осей, то координаты ее центра тяжести можно определить по формулам
Очевидно, что если статический момент плоской фигуры относительно некоторой оси равен нулю, то центр тяжести этой фигуры лежит на этой оси.
ТРЕНИЕ СКОЛЬЖЕНИЯ Угол трения. Конус трения Определение.Углом трения называется угол, образованный нормальной реакцией
Иначе, углом трения называется наибольший угол  , который может образовать полная реакция опорной поверхности с нормалью этой поверхности , который может образовать полная реакция опорной поверхности с нормалью этой поверхности
Полная реакция опорной поверхности всегда расположена в области угла трения (либо внутри угла трения, либо совпадает с одной из сторон этого угла). Видно, что: Таким образом, тангенс угла трения равен коэффициенту трения скольжения. Определение. Конус, ось которого является нормалью к поверхности, а образующая отклонена от нормали на угол, равный углу трения, называется конусом трения (рис. 57). Полная реакция опорной поверхности всегда расположена в области конуса трения (либо внутри конуса, либо совпадает с одной из его образующих). Если при движении тела по неподвижной поверхности в любом направлении коэффициент трения скольжения имеет одно и то же значение, то конус трения будет круговым конусом. Если в разных направлениях коэффициент трения скольжения имеет различные значения, то образующие конуса трения составляют с нормалью опорной поверхности различные углы, поэтому конус трения не будет круговым.
ЛИТЕРАТУРА 1. Тарг С.М. Краткий курс теоретической механики. – М.: " Высшая школа", 1986. –416с. 2. Яблонский А.А., Никифоров В.А. Курс теоретической механики, т.1 – М.: " Высшая школа", 1984, 343с. С О Д Е Р Ж А Н И Е
ВВЕДЕНИЕ 1. ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ…………………… 1.1. Сила и система сил……………………………………………………... 1.2. Аксиомы статики, 2. СВЯЗИ И ИХ РЕАКЦИИ………………………………………………….. 3. СИСТЕМА СХОДЯЩИХСЯ СИЛ………………………………………... 3.1. Теорема о равновесии тела под действием сходящейся системы сил……………………………………………………………... 3.2. Аналитические условия равновесия тела, загруженного сходящейся системой сил……………………………………………… 3.3. Теорема о трех непараллельных силах (правило трех сил)………….. 4. МОМЕНТ СИЛЫ…………………………………………………………... 4.1. Момент силы относительно оси……………………………………….. 4.2. Момент силы относительно полюса (центра, точки)………………… 4.3. Момент силы относительно полюса как векторное произведение……………………………………………………………. 4.4. Связь между моментами силы относительно полюса и относительно оси……………………………………………………….. 4.6 Главный момент системы сил…………………………………………. 4.6. Зависимость между главными моментами системы сил относительно двух полюсов…………………………………………… 4.7. Теорема Вариньона (частный случай)………………………………… 5. ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ СТАТИКИ. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СИЛ……………………………………………………….. 5.1. Элементарные операции статики……………………………………… 5.2. Эквивалентные преобразования. Эквивалентные системы сил. Равнодействующая……………………………………………………… 5.3. Обобщенная теорема Вариньона………………………………………. 6. УСЛОВИЯ РАВНОВЕСИЯ. УСЛОВИЯ РАВНОВЕСИЯ В ОБЩЕМ И ЧАСТНЫХ СЛУЧАЯХ………………………………………………. 6.1. Основная лемма статики………………………………………………… 6.2. Основная теорема статики……………………………………………… 6.3. Аналитические условия равновесия произвольной системы сил 6.4. Частные случаи аналитических условий равновесия…………………. 7. ОБЩИЙ ПРИЗНАК ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СИЛ…… 8. ТЕОРИЯ ПАР СИЛ………………………………………………………….. 8.1. Момент пары сил………………………………………………………… 8.2. Признак эквивалентности двух пар сил………………………………… 8.3. Следствия из признака эквивалентности пар…………………………... 8.4. Теорема о " сложении" пар……………………………………………….. 9. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ……………. 9.1. Лемма о параллельном переносе силы………………………………….. 9.2. Теорема Пуансо……………………………………………………………. 9.3. Частные случаи приведения системы сил к заданному центру………… 9.4. Инварианты системы сил………………………………………………….. 10. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ. ЦЕНТР ТЯЖЕСТИ……………………... 10.1. Центр параллельных сил………………………………………………….. 10.2. Центр тяжести твердого тела……………………………………………… 10.3. Статические моменты……………………………………………………… 10.4. Центры тяжести симметричных тел………………………………………. 10.5. Основные способы определения центра тяжести………………………… 11. ТРЕНИЕ СКОЛЬЖЕНИЯ……………………………………………………... 11.1. Сила трения и коэффициент трения………………………………………. 11.2. Угол трения. Конус трения……………………………………………….... ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ Сила и система сил Сила – векторная величина, являющаяся мерой механического действия одного материального тела на другое. Всякая сила характеризуется величиной, направлением и точкой приложения. Сила – приложенный вектор. Линия действия силы – прямая, проходящая через точку приложения силы и вдоль которой расположена сила. Системой сил называется совокупность сил, приложенных к твердому телу. Обозначение: Две параллельные силы, равные по величине, направленные в противоположные стороны, называются парой сил, или просто парой (рис. 1).
Две силы, равные по величине, направленные в противоположные стороны и имеющие общую линию действия, называются прямо противоположными
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся системой сил(рис. 3). Точка Система сил, линии действия которых параллельны между собой, называется системой параллельных сил. Кроме сходящихся и параллельных систем сил различают произвольные системы сил– это системы сил, линии действия которыхрасположены как угодно в пространстве (пространственная система сил) или на плоскости (плоская система сил). Всякой силе ставится в соответствие свободный вектор – вектор силы. Вектором силы называется свободный вектор, параллельный силе, направленный в ту же сторону и имеющий длину, равную длине силы. Главным вектором системы сил называется свободный вектор, равный геометрической сумме векторов сил, составляющих систему. Обозначение: Если задана система сил
Популярное:
|
Последнее изменение этой страницы: 2016-05-30; Просмотров: 975; Нарушение авторского права страницы