Расчет основных конструктивных точек
Чертеж конструкции одежды представляет собой совокупность графических примитивов, следовательно, необходимо выделить отдельные графические элементы и описать их математически.
При конструировании одежды чаще всего используют такие примитивы, как отрезок, дуга, ломаная, лекальная кривая.
Чертеж брюк представлен на рисунке 1.
Конструктивные точки будем обозначать Рi, а их координаты – xi, yi.
Перед началом расчетов задаем систему координат т.е. определяем положение точки начала координат и направление осей. За начало системы координат удобнее брать точку, с которой начинается построение чертежа.
Расчет координат конструктивных точек представлен в таблице 1.17, а типы примитивов в таблице 1.18.
Таблица 1.17- Расчет координат точек и переменных

| Р8
| Х8=Х7=14, 4; Y8= Y2=20, 0
| 14, 4; 20, 0
| | Р9
| Х9= Х8=14, 4; Y9= Y4=60, 5
| 14, 4; 60, 5
| | Р10
| Х10= Х9=14, 4; Y10= Y1=104, 5
| 14, 4; 104, 5
| | Р11
| Х11= Х10-((0, 5*Шн-2)/2))=
=14, 4-((0, 5*48-2)/2))=3, 4; Y11= Y10=104, 5
| 3, 4; 104, 5
| | Р12
| Х12= Х10+((0, 5*Шн-2)/2))=
=14, 4+((0, 5*48-2)/2))=25, 4
Y12= Y11=104, 5
| 25, 4; 104, 5
|
Продолжение таблицы 1.17
|
|
|
| | Р13
| Х13= Х9-((0, 5*Шк-2)/2)=
=14, 4-((0, 5*44-2)/2)=3, 4;
Y13= Y9=60, 5
| 3, 4; 60, 5
| | Р14
| Х14= Х9+((0, 5*Шк-2)/2)=
=14, 4+((0, 5*44-2)/2)=24, 4
Y14= Y13=60, 5
| 24, 4; 60, 5
| | Р15
| Х15= Х5-((0, 1*(Сб+Пб))=
=28, 8-((0, 1*(50+0, 5))=23, 7
Y15= Y6=27, 6
| 23, 7; 27, 6
| | Р16
| Х16= Х15=23, 7
Y16= Y8=20, 0
| 23, 7; 20, 0
| | Р17
| Х17= Х16=23, 7
Y17=0
| 23, 7; 0
| | Р18
| Х18= Х17=23, 7
Y18=1
| 23, 7; 1
| | R1
| Окружность с центром в точке Р18 и радиусом R1=((0, 5*(Ст+Пт)-1))+1, (р-р. выт.)+, (р-р. выт.)=((0, 5*(3, 59+1))+1+2=20, 4
| 20, 4
| | Р19
| На пересечении окружности с центром в точке Р18 и отрезка Р0Р7
|
| | R2
| Окружность с центром в точке Р19 и радиусом R2=((0, 5*(Ст+Пт)-1))+р-р. выт.= =((0, 5*(35, 9+1-1))+2=19, 4
| 19, 4
| | Р20
| На пересечении окружности с центром в точке Р19 и отрезка Р19Р18
|
| | Р21
| Прямоуг. треугольник Р19Р17 Р18, ( Р19Р17)2=
=( Р19Р18)2-( Р17Р18)2; Р19Р17= 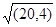 2-12=
=20, 3; Х19 =Х17-20, 3=23, 7-20, 3=3, 4;
Р19Р17=Х7-Х19=14, 4-3, 4=11;
Треугольник Р17Р18 Р19~треугольник Р19Р7 Р21; Р17Р18/ Р7Р21= Р17Р19/ Р19Р7; 1/ Р7Р21=
=20, 3/11; Р7Р21= 0, 5 следовательно Х21= Х10=14, 4; Y21=0, 5. 2-12=
=20, 3; Х19 =Х17-20, 3=23, 7-20, 3=3, 4;
Р19Р17=Х7-Х19=14, 4-3, 4=11;
Треугольник Р17Р18 Р19~треугольник Р19Р7 Р21; Р17Р18/ Р7Р21= Р17Р19/ Р19Р7; 1/ Р7Р21=
=20, 3/11; Р7Р21= 0, 5 следовательно Х21= Х10=14, 4; Y21=0, 5.
| 14, 4; 0, 5
| | R3
| Окружность с центром в точке Р21 и радиусом R3=1/2 р-ра.выт.=1/2*2=1
|
| | Р22
| На пересечении окружности в центром в точке Р21 и отрезка Р21Р20
|
| | R4
| Окружность с центром в точке Р21 и радиусом R4=1/2 р-ра.выт.=1/2*2=1
|
| | Р23
| На пересечении окружности с центром в точке Р21 и отрезка Р21Р19
|
| | Р24
| Х24= Х21=14, 4
Y24= Y21+длина выт.=0, 5+8=8, 5
| 14, 4; 8, 5
| | Р25
| Х25= Х16+0, 5=23, 7+0, 5=24, 2
Y25= Y16=20, 0
| 24, 2; 20, 0
| Продолжение таблицы 1.17
|
|
|
| | R5
| Окружность с центром в точке Р25 и радиусом R5=1/2 Р25Р5 введем дополнительные точки Р15`; Х15`=Х25=24, 2; Y15`= Y15=27.6.
Р`15=Р5=Х5-Х15`=28, 8-24, 2=4, 6;
Р`15Р25=Y`15-Y25=27, 6-20=7, 6;
Треугольник Р25Р5 Р`15-прямоуг.;
(Р25Р5)2=( Р15 `Р25)2+( Р15Р5)2;
Р25Р5= 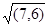 2+ 2+ 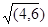 2=8, 8
R5=1/2*8, 8=4, 4. 2=8, 8
R5=1/2*8, 8=4, 4.
| 4, 4
| | Р26
| На пресечении окружности с центром в точке Р25 и отрезок Р7Р17
|
| | R6
| Окружность с центром в точке Р15 и радиусом R6=2/3 Р15Р26 введем дополнительные точки Р15``; Х``15=Х5=28.8; Y15``= Y25=20.0.
Треугольник Р15 Р15``Р5- прямоуг.
(Р15Р15``)2=( Р15 Р5)2+( Р5Р15``)2;
Р15Р5=Х5-Х15=28, 8-23, 7=5, 1;
Р15 ``Р5= Р25Р`15=7, 6;
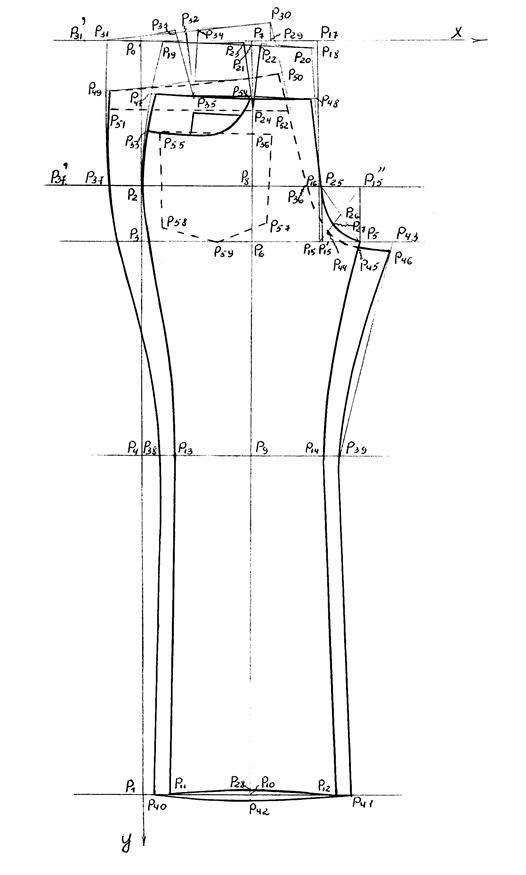
Р15 Р5``= 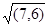 2+ 2+ 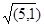 2=9, 1
Р15Р26=1/2 *Р15Р15``=9, 1*1/2=4, 55;
R6=2/3*4, 55=3.. 2=9, 1
Р15Р26=1/2 *Р15Р15``=9, 1*1/2=4, 55;
R6=2/3*4, 55=3..
|
| | Р27
| На пресечении окружности с центром в точке Р15 и отрезок Р15Р26
|
| | Р28
| Х28= Х10=14, 4
Y28= Y12-0, 5=104, 5-0, 5=104
| 14, 4; 104
| | Р29
| введем дополнительные точки Р`20; Х`20=Х17-1=23, 7-1=22, 7; Y`20= 0
Х29=1/3*(Х`20-Х7)+ Х7=1/3*(22, 7-
-14, 4)+14, 4=.17, 1;
Y29=0.
| 17, 1; 0
| | Р30
| Х30= Х29=17, 1;
Y30=-(0, 05*Сб+1-(Дсб-Дсз))= =0, 05*50+1, 0+1, 3=-2, 2;
| 17, 1; -2, 2
| | R7
| Окружность с центром в точке Р30 и радиусом R7=0, 5*(Ст+Пт)+1+р-р. выт.=
=0, 5*(35, 9+1)+1+3=22, 4 введем дополнит. точки Р`31; Х`31=(-7, 5); Y`31=0.
| 22.4
| | Р31
| На пресечении окружности с центром в точке Р30 и отрезок Р0Р`31
|
| | R8
| Окружность с центром в точке Р30 и радиусом R8=1/2 R7=1/2*22.4=11, 2
| 11, 2
| | Р32
| На пресечении окружности с центром в точке Р30 и отрезок РР30Р31
|
| | R9
| Окружность с центром в точке Р32 и радиусом R9=1/2р-ра. выт. =1/2*3=1, 5
| 1, 5
| Продолжение таблицы 1.17
|
|
|
| | Р33
| На пресечении окружности с центром в точке Р32 и отрезка Р32 Р31
|
| | R10
| Окружность с центром в точке Р32 и радиусом R10=1/2р-ра. выт. =1/2*3=1, 5
| 1, 5
| | Р34
| На пресечении окружности с центром в точке Р32 и отрезка Р32 Р30 к отрезку Р31 Р30
В точке Р32 восстанавливаем перпендикуляр
|
| | R11
| Окружность с центром в точке Р32 и радиусом R11=длина выт-ки=10, 0
| 10, 0
| | Р35
| На пресечении окружности с центром в точке Р32 и перпен-ра восстановленного к отрезку Р31 Р30 в точке Р32
|
| | Р36
| На пресечении отрезка Р25 Р8 и отрезка Р30 Р15
|
| | R12
| Окружность с центром в точке Р36 и радиусом R12=(Сб+Пб)-Х25=(50+0, 5)-23, 5=27;
Введем дополнительные точки Р37`;
Х`37=(-10); Y`37=20
|
| | Р37
| На пресечении окружности с центром в точке Р36 и отрезка Р2 Р`37
|
| | Р38
| Х38= Х9-((0, 5*Шк+2)/2)=
=14, 4-((0, 5*44+2)/2)=2, 4;
Y38= Y13=60, 5
| 2, 4; 60, 5
| | Р39
| Х39= Х9+((0, 5*Шк+2)/2)=
=14, 4+((0, 5*44+2)/2)=26, 4;
Y39= Y38=60, 5
| 26, 4; 60, 5
| | Р40
| Х40= Х10-((0, 5*Шн+2)/2))=
=14, 4-((0, 5*48+2)/2))=1, 4
Y40= Y10=104, 5
| 1, 4; 104, 5
| | Р41
| Х41= Х10+((0, 5*Шн+2)/2))=
=14, 4+((0, 5*48+2)/2))=27, 4
Y41= Y40=104, 5
| 27, 4; 104, 5
| | Р42
| Х42= Х10=14, 4;
Y42= Y10+0, 5=104, 5+0, 5=105
| 14, 4; 105
| | Р43
| Х43= Х15+0, 2*(Сб+Пб)=23, 7+0, 2*(50+0, 5)=
=33, 8; Y43= Y15=27, 6
| 33, 8; 27, 6
| | R13
| Окружность с центром в точке Р15 и радиусом R13=1, 5
| 1, 5
| | Р44
| На пресечении окружности с центром в точке Р15 и отрезка Р15Р26
|
| | R14
| Окружность с центром в точке Р5 и радиусом R14=1, 0
| 1, 0
| | Р45
| На пресечении окружности с центром в точке Р5 и полилинии Р5Р14
|
| Окончание таблицы 1.17
|
|
|
| | Р46
| На пресечении прямой Р15Р45 и отрезка Р43Р39
|
|
1.6.3 Описание геометрических построений (графических примитивов)
Чертеж состоит из набора графических примитивов, под которыми понимается элемент чертежа, обрабатываемый системой как целое, а не как совокупность точек или объектов. При построении данного чертежа использовались такие примитивы, как отрезок, окружность, кривая и зеркало.
Таблица 1.18-Описание графических примитивов.
| Тип примитива
| Конструктивные точки
| |
|
| | Отрезок
| Р0Р1; Р0Р2; Р0Р3; Р0Р1; Р0Р4; Р3Р5; Р3Р6;
Р0Р7; Р2Р8; Р7Р9; Р7Р10; Р1Р11; Р1Р12; Р4Р13; Р4Р14; Р3Р15; Р2Р16; Р0Р17; Р17Р18;
Р7Р21; Р21Р24; Р2Р25; Р7Р28; Р0Р29; Р29Р30;
Р0Р31`; Р2Р37`; Р4Р38; Р4Р39; Р1Р40; Р1Р41;
Р7Р42; Р3Р43.
| | Окружность
| Из точки Р18→ R1=20, 4
Из точки Р19→ R2=19, 4
Из точки Р21→ R3=1, 0
Из точки Р21→ R4=1, 0
Из точки Р25→ R5=4, 4
Из точки Р15→ R6=3, 0
Из точки Р30→ R7=22, 4
Из точки Р30→ R8=11, 2
Из точки Р32→ R9=1, 5
Из точки Р32→ R10=1, 5
Из точки Р32→ R11=10, 0
Из точки Р25→ R12=27
Из точки Р15→ R13=1, 5
Из точки Р5→ R14=1, 0
| |
Окончание таблицы 1.18
| | |
|
| | Кривая
| Р31Р49Р37 Р38; Р19Р47Р2 Р13; Р5Р44Р14;
Р43Р46Р39; Р20Р25Р27 Р5; Р30Р50Р36Р44Р46.
Р11Р28Р12; Р40Р42Р41
| |
Зеркало
| Р11-Р12; Р13-Р14; Р23-Р22; Р40-Р41;
Р38-Р39; Р33-Р34.
| | | | |
Внедрение автоматизированных систем способствует сокращению или замене ручного труда машинным в различных сферах производственной деятельности, что в конечном результате позволяет избавить человека от выполнения рутинных работ, сделать труд более интеллектуальным и творческим, повысить производительность труда и качество продукции. Это не подразумевает полного вытеснения человека автоматизированной системой из технологического процесса, а предполагает их разумное взаимодействие.
Использование графических программ обеспечивает сокращение трудоемкости проектирования в несколько раз, но для этого необходима предварительная подготовка программы на Автолисте, затраты времени на создание которой значительно превосходит время при разработке чертежа в режиме графического редактора. Поэтому графическое программирование дает эффект в тех случаях, когда в конструкторских подразделениях проектируется большое количество однотипных изделий, различающихся значениями размеров и (в заранее определенных пределах) вариантами исполнения.
Выполненные расчеты могут применяться в построении лекал деталей, а также при разработке производных и вспомогательных лекал.

Популярное:
|

