Непрерывные случайные величины
Непрерывная СВ (НСВ) – это величина, множество возможных значений которой – непрерывное множество, т.е. сплошь заполняет некоторый промежуток (определение не строгое). Можно показать, что вероятность отдельного значения НСВ равна нулю. Из этого не следует, что событие невозможное. Это означает, что при неограниченном повторении опыта это событие будет появляться сколь угодно редко.
Универсальным законом распределения, пригодным как для ДСВ, так и для НСВ, который полностью характеризует СВ с вероятностной точки зрения, является функция распределения  . .
Свойства функции распределения
1. Функция распределения  , что следует из определения функции распределения, как вероятности события , что следует из определения функции распределения, как вероятности события  , а вероятность любого события , а вероятность любого события  . .
2. Функция распределения неубывающая функция своего аргумента, т.е. если  , то , то 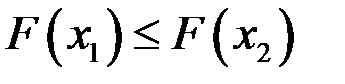 . .
3. Вероятность попадания СВ в промежуток  равна приращению функции распределения на этом интервале равна приращению функции распределения на этом интервале
 . .
4. Если возможные значения СВ принадлежат интервалу  , то , то
1)  при при  , 2) , 2)  при при  . .
5. Если возможные значения НСВ расположены на всей оси Ох, то
 , ,  . .
6. Функция  непрерывна слева, т.е. непрерывна слева, т.е.  . Для непрерывной СВ функция распределения непрерывна всюду. . Для непрерывной СВ функция распределения непрерывна всюду.
Замечание. Так как вероятность каждого отдельного значения НСВ равна нулю, то для НСВ справедливы равенства
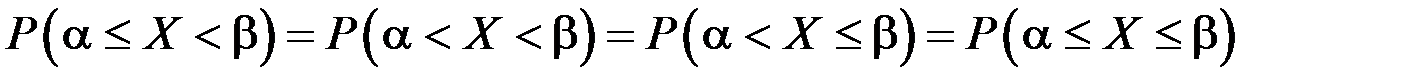 . .
Плотностью распределения (или плотностью вероятности, или плотностью) НСВ Х в точке х называется производная ее функции распределения в этой точке:
 . .
График плотности распределения называется кривой распределения. Плотность распределения существует только для НСВ.
Плотность распределения называют дифференциальной функцией распределения или дифференциальным законом распределения.
Свойства плотности распределения
1. Плотность распределения – неотрицательная функция, т.е.  . .
2. Вероятность попадания СВ с плотностью распределения  в данный интервал в данный интервал  выражается формулой: выражается формулой:
 . .
3. Функция распределения выражается через плотность распределения формулой:
 . .
4. Интеграл в бесконечных пределах от плотности распределения равен единице (свойство нормированности):
 . .
Замечание. Если функция  не удовлетворяет свойству 4, то она не может быть плотностью распределения какой-либо случайной величины. не удовлетворяет свойству 4, то она не может быть плотностью распределения какой-либо случайной величины.
Числовые характеристики НСВ
Математическое ожидание для НСВ, все значения которой принадлежат отрезку 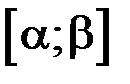 определяется формулой: определяется формулой:
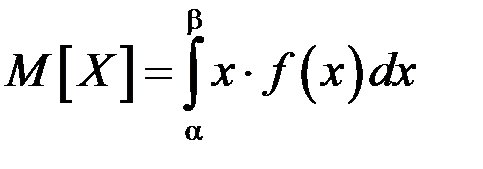 . .
Если все значения непрерывной случайной величины принадлежат промежутку  , то математическое ожидание определяется формулой: , то математическое ожидание определяется формулой:
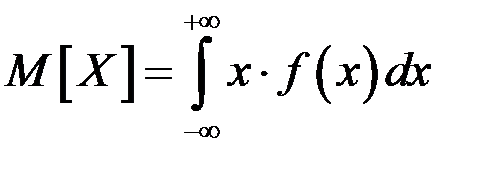 , ,
если несобственный интеграл сходится абсолютно
Дисперсия НСВ, все значения которой принадлежат отрезку 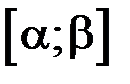 , определяется формулой , определяется формулой
 . .
Если непрерывная случайная величина принимает значения, принадлежащие промежутку 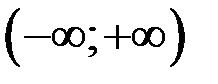 , то ее дисперсия определяется формулой , то ее дисперсия определяется формулой
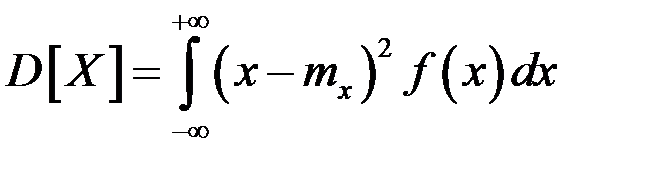 , ,
если несобственный интеграл сходится абсолютно.
Среднее квадратическое отклонение случайной величины находится по формуле
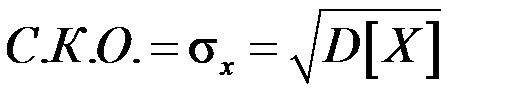 . .
Пример
Плотность распределения непрерывной случайной величины Х имеет вид
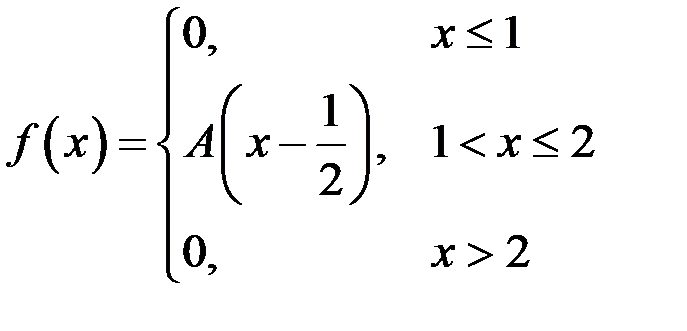 . .
Найти: параметр А, функцию распределения  , вероятность попадания случайной величины Х в интервал , вероятность попадания случайной величины Х в интервал 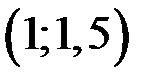 , математическое ожидание , математическое ожидание 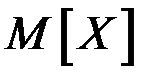 и дисперсию и дисперсию 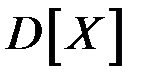 . .
Решение
Для определения значения А воспользуемся условием 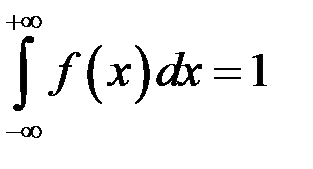 . Вычислим интеграл . Вычислим интеграл
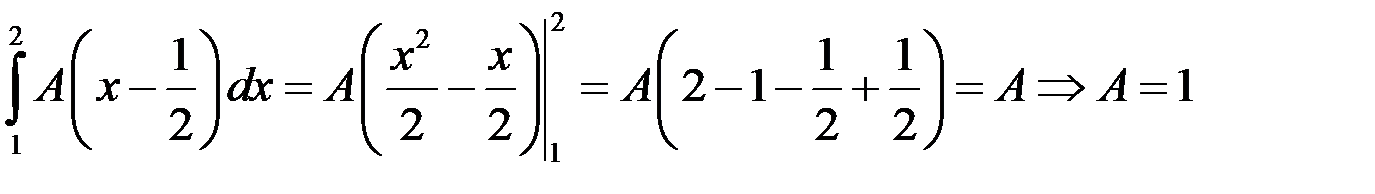 , ,
плотность распределения случайной величины Х примет вид
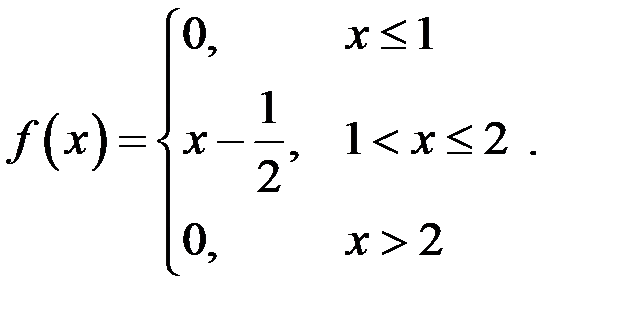
Для того, чтобы найти функцию распределения  , воспользуемся формулой , воспользуемся формулой 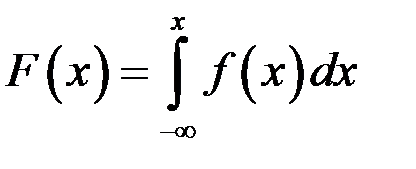 . .
При  получаем получаем 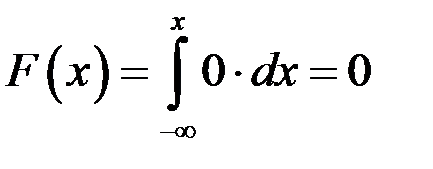 , ,
при  находим находим 
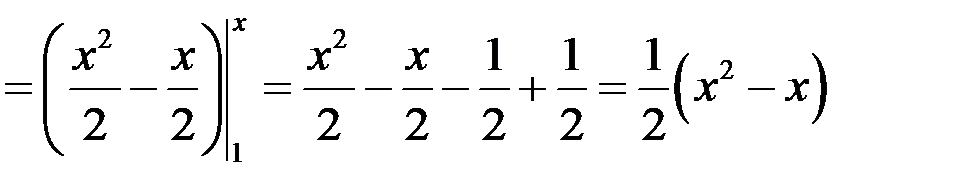 , ,
при 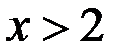 : : 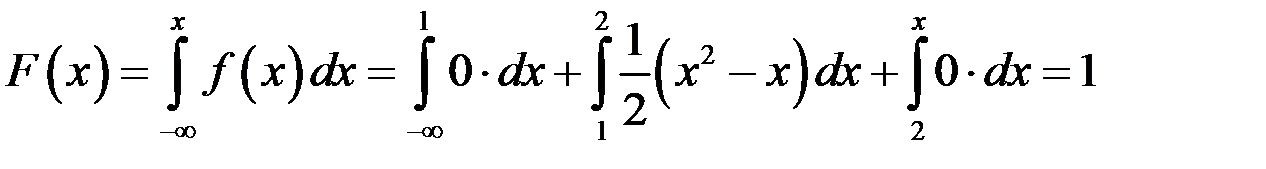 . .
Таким образом, искомая функция распределения имеет вид
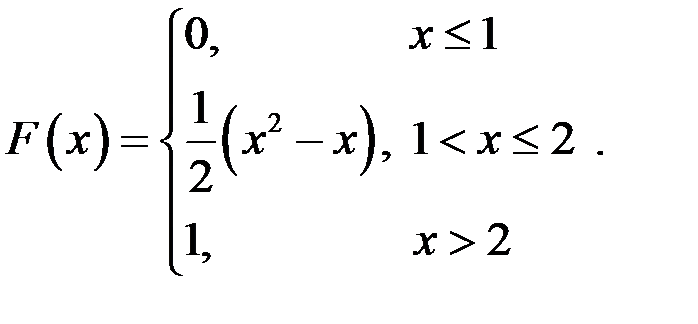
Вероятность попадания СВ Х в интервал  найдем по формуле найдем по формуле 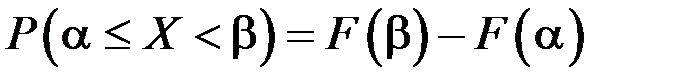 , она будет равна , она будет равна
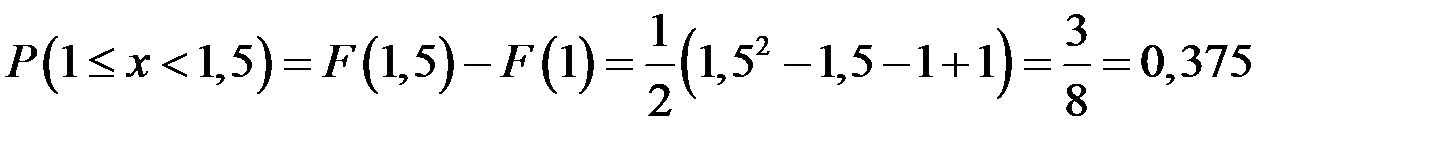 . .
Математическое ожидание находим по формуле 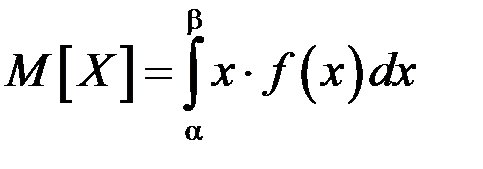 : :
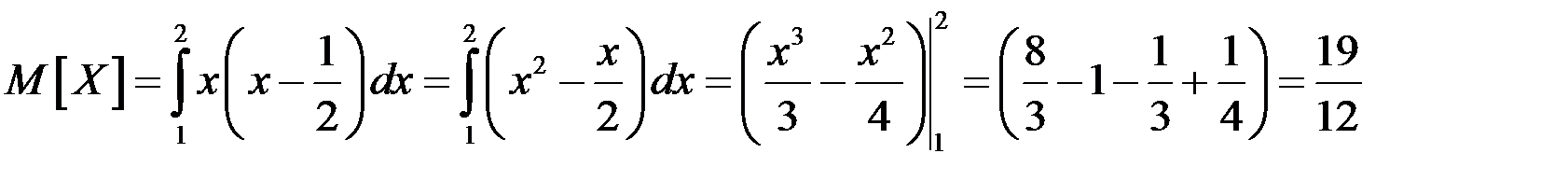 . .
Дисперсию найдем по формуле 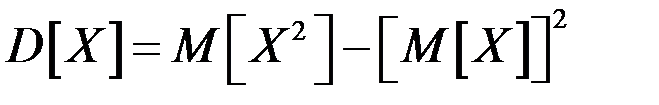 : :
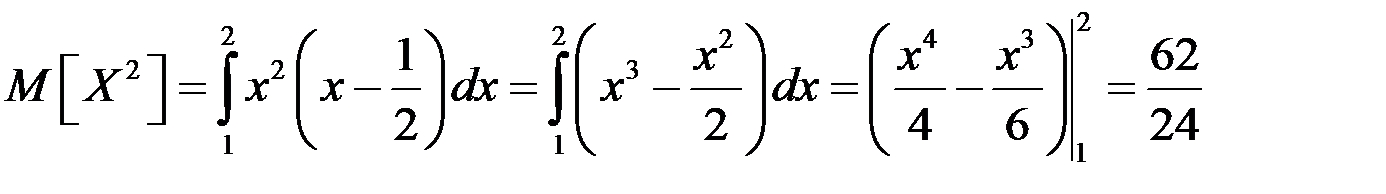 , ,
тогда 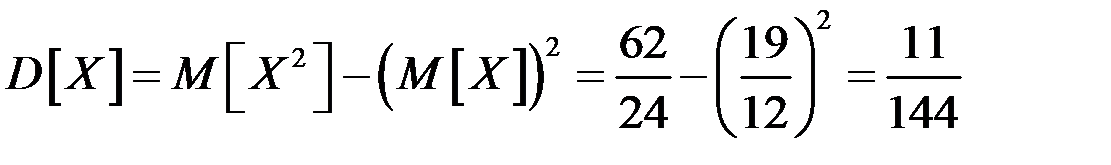 . .
Краткое содержание (программа) курса
Теория вероятностей
Элементы комбинаторики (размещения, сочетания, перестановки). Основные понятия теории вероятностей. Алгебра событий. Аксиомы теории вероятностей. Следствия из аксиом теории вероятностей. Классическое определение вероятности. Геометрическое определение вероятности. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей. Теорема сложения вероятностей. Формула полной вероятности. Формулы Байеса. Последовательность независимых испытаний. Формула Бернулли. Следствия из формулы Бернулли. Формула Пуассона.
Понятие случайной величины (СВ) и ее закона распределения. ДСВ и НСВ. Ряд распределения. Многоугольник распределения. Функции распределения, ее свойства. Плотность распределения, ее свойства. Числовые характеристики СВ (математическое ожидание, мода, медиана, дисперсия, СКО). Начальные и центральные моменты СВ. Биномиальное распределение. Распределение Пуассона. Равномерное распределение. Показательное распределение. Нормальный закон распределения и его параметры. Вероятность попадания СВ, подчиненной нормальному закону, на заданный участок. Функция Лапласа. Дискретные и непрерывные системы случайных величин (ССВ). Система 2-х СВ, матрица распределения. Функция распределения двумерной СВ, ее свойства. Числовые характеристики ССВ. Корреляционный момент, коэффициент корреляции, корреляционная матрица. Закон больших чисел. Предельные теоремы.
Приложение 1
Значения функции Лапласа
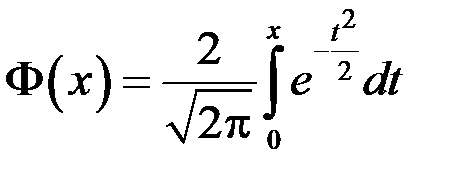
| х
| F(х)
| х
| F(х)
| х
| F(х)
| х
| F(х)
| | 0, 00
| 0, 0000
| 0, 30
| 0, 2358
| 0, 60
| 0, 4515
| 0, 90
| 0, 6319
| | 0, 01
| 0, 0080
| 0, 31
| 0, 2434
| 0, 61
| 0, 4581
| 0, 91
| 0, 6372
| | 0, 02
| 0, 0160
| 0, 32
| 0, 2510
| 0, 62
| 0, 4647
| 0, 92
| 0, 6424
| | 0, 03
| 0, 0239
| 0, 33
| 0, 2586
| 0, 63
| 0, 4713
| 0, 93
| 0, 6476
| | 0, 04
| 0, 0319
| 0, 34
| 0, 2661
| 0, 64
| 0, 4878
| 0, 94
| 0, 6528
| | 0, 05
| 0, 0399
| 0, 35
| 0, 2737
| 0, 65
| 0, 4843
| 0, 95
| 0, 6579
| | 0, 06
| 0, 0478
| 0, 36
| 0, 2812
| 0, 66
| 0, 4907
| 0, 96
| 0, 6629
| | 0, 07
| 0, 0558
| 0, 37
| 0, 2886
| 0, 67
| 0, 4971
| 0, 97
| 0, 6680
| | 0, 08
| 0, 0638
| 0, 38
| 0, 2961
| 0, 68
| 0, 5035
| 0, 98
| 0, 6729
| | 0, 09
| 0, 0717
| 0, 39
| 0, 3035
| 0, 69
| 0, 5098
| 0, 99
| 0, 6778
| | 0, 10
| 0, 0797
| 0, 40
| 0, 3108
| 0, 70
| 0, 5161
| 1, 00
| 0, 6827
| | 0, 11
| 0, 0876
| 0, 41
| 0, 3182
| 0, 71
| 0, 5223
| 1, 01
| 0, 6875
| | 0, 12
| 0, 0955
| 0, 42
| 0, 3255
| 0, 72
| 0, 5285
| 1, 02
| 0, 6923
| | 0, 13
| 0, 1034
| 0, 43
| 0, 3328
| 0, 73
| 0, 5346
| 1, 03
| 0, 6970
| | 0, 14
| 0, 1113
| 0, 44
| 0, 3401
| 0, 74
| 0, 5407
| 1, 04
| 0, 7017
| | 0, 15
| 0, 1192
| 0, 45
| 0, 3473
| 0, 75
| 0, 5467
| 1, 05
| 0, 7063
| | 0, 16
| 0, 1271
| 0, 46
| 0, 3545
| 0, 76
| 0, 5527
| 1, 06
| 0, 7109
| | 0, 17
| 0, 1350
| 0, 47
| 0, 3616
| 0, 77
| 0, 5587
| 1, 07
| 0, 7154
| | 0, 18
| 0, 1428
| 0, 48
| 0, 3688
| 0, 78
| 0, 5646
| 1, 08
| 0, 7199
| | 0, 19
| 0, 1507
| 0, 49
| 0, 3759
| 0, 79
| 0, 5705
| 1, 09
| 0, 7243
| | 0, 20
| 0, 1585
| 0, 50
| 0, 3829
| 0, 80
| 0, 5763
| 1, 10
| 0, 7287
| | 0, 21
| 0, 1663
| 0, 51
| 0, 3899
| 0, 81
| 0, 5821
| 1, 11
| 0, 7330
| | 0, 22
| 0, 1741
| 0, 52
| 0, 3969
| 0, 82
| 0, 5878
| 1, 12
| 0, 7373
| | 0, 23
| 0, 1819
| 0, 53
| 0, 4039
| 0, 83
| 0, 5935
| 1, 13
| 0, 7415
| | 0, 24
| 0, 1897
| 0, 54
| 0, 4108
| 0, 84
| 0, 5991
| 1, 14
| 0, 7457
| | 0, 25
| 0, 1974
| 0, 55
| 0, 4177
| 0, 85
| 0, 6047
| 1, 15
| 0, 7499
| | 0, 26
| 0, 2051
| 0, 56
| 0, 4245
| 0, 86
| 0, 6102
| 1, 16
| 0, 7540
| | 0, 27
| 0, 2128
| 0, 57
| 0, 4313
| 0, 87
| 0, 6157
| 1, 17
| 0, 7580
| | 0, 28
| 0, 2205
| 0, 58
| 0, 4381
| 0, 88
| 0, 6211
| 1, 18
| 0, 7620
| | 0, 29
| 0, 2282
| 0, 59
| 0, 4448
| 0, 89
| 0, 6265
| 1, 19
| 0, 7660
| | х
| F(х)
| х
| F(х)
| х
| F(х)
| х
| F(х)
| | 1, 20
| 0, 7699
| 1, 50
| 0, 8664
| 1, 80
| 0, 9281
| 2, 50
| 0, 9876
| | 1, 21
| 0, 7737
| 1, 51
| 0, 8690
| 1, 81
| 0, 9297
| 2, 55
| 0, 9892
| | 1, 22
| 0, 7775
| 1, 52
| 0, 8715
| 1, 82
| 0, 9312
| 2, 60
| 0, 9907
| | 1, 23
| 0, 7813
| 1, 53
| 0, 8740
| 1, 83
| 0, 9328
| 2, 65
| 0, 9920
| | 1, 24
| 0, 7850
| 1, 54
| 0, 8764
| 1, 84
| 0, 9342
| 2, 70
| 0, 9931
| | 1, 25
| 0, 7887
| 1, 55
| 0, 8789
| 1, 85
| 0, 9357
| 2, 75
| 0, 9940
| | 1, 26
| 0, 7923
| 1, 56
| 0, 8812
| 1, 86
| 0, 9371
| 2, 80
| 0, 9949
| | 1, 27
| 0, 7959
| 1, 57
| 0, 8836
| 1, 87
| 0, 9385
| 2, 85
| 0, 9956
| | 1, 28
| 0, 7995
| 1, 58
| 0, 8859
| 1, 88
| 0, 9399
| 2, 90
| 0, 9963
| | 1, 29
| 0, 8029
| 1, 59
| 0, 8882
| 1, 89
| 0, 9412
| 2, 95
| 0, 9968
| | 1, 30
| 0, 8064
| 1, 60
| 0, 8904
| 1, 90
| 0, 9426
| 3, 00
| 0, 9973
| | 1, 31
| 0, 8098
| 1, 61
| 0, 8926
| 1, 91
| 0, 9432
| 3, 10
| 0, 9981
| | 1, 32
| 0, 8132
| 1, 62
| 0, 8948
| 1, 92
| 0, 9451
| 3, 20
| 0, 9986
| | 1, 33
| 0, 8165
| 1, 63
| 0, 8969
| 1, 93
| 0, 9464
| 3, 30
| 0, 9990
| | 1, 34
| 0, 8198
| 1, 64
| 0, 8990
| 1, 94
| 0, 9476
| 3, 40
| 0, 9993
| | 1, 35
| 0, 8230
| 1, 65
| 0, 9011
| 1, 95
| 0, 9488
| 3, 50
| 0, 9995
| | 1, 36
| 0, 8262
| 1, 66
| 0, 9031
| 1, 96
| 0, 9500
| 3, 60
| 0, 9997
| | 1, 37
| 0, 8293
| 1, 67
| 0, 9051
| 1, 97
| 0, 9512
| 3, 70
| 0, 9998
| | 1, 38
| 0, 8324
| 1, 68
| 0, 9070
| 1, 98
| 0, 9523
| 3, 80
| 0, 9999
| | 1, 39
| 0, 8355
| 1, 69
| 0, 9090
| 1, 99
| 0, 9534
| 3, 90
| 0, 9999
| | 1, 40
| 0, 8385
| 1, 70
| 0, 9109
| 2, 00
| 0, 9545
| 4, 00
| 0, 9999
| | 1, 41
| 0, 8415
| 1, 71
|
| 2, 05
| 0, 9596
| 4, 42
| 1-10-5
| | 1, 42
| 0, 8444
| 1, 72
| 0, 9146
| 2, 10
| 0, 9643
| 4, 89
| 1-10-6
| | 1, 43
| 0, 8473
| 1, 73
| 0, 9164
| 2, 15
| 0, 9684
| 5, 33
| 1-10-7
| | 1, 44
| 0, 8501
| 1, 74
| 0, 9181
| 2, 20
| 0, 9722
|
|
| | 1, 45
| 0, 8529
| 1, 75
| 0, 9199
| 2, 25
| 0, 9756
|
|
| | 1, 46
| 0, 8557
| 1, 76
| 0, 9216
| 2, 30
| 0, 9786
|
|
| | 1, 47
| 0, 8584
| 1, 77
| 0, 9233
| 2, 35
| 0, 9812
|
|
| | 1, 48
| 0, 8611
| 1, 78
| 0, 9249
| 2, 40
| 0, 9836
|
|
| | 1, 49
| 0, 8638
| 1, 79
| 0, 9265
| 2, 45
| 0, 9857
|
|
|
Приложение 2
Таблица значений c2 в зависимости от r=n-1 и p.
| | р
| | n-1
| 0, 99
| 0, 98
| 0, 95
| 0, 90
| 0, 80
| 0, 70
| 0, 50
| 0, 30
| 0, 20
| 0, 10
| 0, 05
| 0, 02
| 0, 01
| 0, 001
| |
| 0, 000
| 0, 001
| 0, 004
| 0, 016
| 0, 064
| 0, 148
| 0, 455
| 1, 074
| 1, 642
| 2, 71
| 3, 84
| 5, 41
| 6, 64
| 10, 83
| |
| 0, 020
| 0, 040
| 0, 103
| 0, 211
| 0, 446
| 0, 713
| 1, 386
| 2, 41
| 3, 22
| 4, 60
| 5, 99
| 7, 82
| 9, 21
| 13, 82
| |
| 0, 115
| 0, 185
| 0, 352
| 0, 584
| 1, 005
| 1, 424
| 2, 37
| 3, 66
| 4, 64
| 6, 25
| 7, 82
| 9, 34
| 11, 84
| 16, 27
| |
| 0, 297
| 0, 429
| 0, 711
| 1, 064
| 1, 649
| 2, 20
| 3, 36
| 4, 88
| 5, 99
| 7, 78
| 9, 49
| 11, 67
| 13, 28
| 18, 46
| |
| 0, 554
| 0, 752
| 1, 145
| 1, 610
| 2, 34
| 3, 00
| 4, 35
| 6, 06
| 7, 29
| 9, 24
| 11, 07
| 13, 39
| 15, 09
| 20, 5
| |
| 0, 872
| 1, 134
| 1, 635
| 2, 20
| 3, 07
| 3, 93
| 5, 35
| 7, 23
| 8, 56
| 10, 64
| 12, 59
| 15, 03
| 16, 81
| 22, 5
| |
| 1, 239
| 1, 564
| 2, 17
| 2, 83
| 3, 82
| 4, 67
| 6, 35
| 8, 38
| 9, 80
| 12, 02
| 14, 07
| 16, 62
| 18, 48
| 24, 3
| |
| 1, 646
| 2, 03
| 2, 73
| 3, 49
| 4, 59
| 5, 53
| 7, 34
| 9, 52
| 11, 03
| 13, 36
| 15, 51
| 18, 17
| 20, 1
| 26, 1
| |
| 2, 09
| 2, 53
| 3, 32
| 4, 17
| 5, 38
| 6, 39
| 8, 34
| 10, 66
| 12, 24
| 14, 68
| 16, 92
| 19, 68
| 21, 7
| 27, 9
| |
| 2, 56
| 3, 06
| 3, 94
| 4, 86
| 6, 18
| 7, 27
| 9, 34
| 11, 78
| 13, 44
| 15, 99
| 18, 31
| 21, 2
| 23, 2
| 29, 6
| |
| 3, 05
| 3, 61
| 4, 58
| 5, 58
| 6, 99
| 8, 15
| 10, 34
| 12, 90
| 14, 63
| 17, 28
| 19, 68
| 22, 6
| 24, 7
| 31, 3
| |
| 3, 57
| 4, 18
| 5, 23
| 6, 30
| 7, 81
| 9, 03
| 11, 34
| 14, 01
| 15, 81
| 18, 55
| 21, 0
| 24, 1
| 26, 2
| 32, 9
| |
| 4, 11
| 4, 76
| 5, 89
| 7, 04
| 8, 63
| 9, 93
| 12, 34
| 15, 12
| 16, 98
| 19, 81
| 22, 4
| 25, 5
| 27, 7
| 34, 6
| |
| 4, 66
| 5, 37
| 6, 57
| 7, 79
| 9, 47
| 10, 82
| 13, 34
| 16, 22
| 18, 15
| 21, 1
| 23, 7
| 26, 9
| 29, 1
| 36, 1
| |
| 5, 23
| 5, 98
| 7, 26
| 8, 55
| 10, 31
| 11, 72
| 14, 34
| 17, 32
| 19, 31
| 22, 3
| 25, 0
| 28, 3
| 30, 6
| 37, 7
| |
| 5, 81
| 6, 61
| 7, 96
| 9, 31
| 11, 15
| 12, 62
| 15, 34
| 18, 42
| 20, 5
| 23, 5
| 26, 3
| 29, 6
| 32, 0
| 39, 3
| |
| 6, 41
| 7, 26
| 8, 67
| 10, 08
| 12, 00
| 13, 53
| 16, 34
| 19, 51
| 21, 6
| 24, 8
| 27, 6
| 31, 0
| 33, 4
| 40, 8
| |
| 7, 02
| 7, 91
| 9, 39
| 10, 86
| 12, 86
| 14, 44
| 17, 34
| 20, 6
| 22, 8
| 26, 0
| 28, 9
| 32, 3
| 34, 8
| 42, 3
| |
| 7, 63
| 8, 57
| 10, 11
| 11, 65
| 13, 72
| 15, 35
| 18, 34
| 21, 7
| 23, 9
| 27, 2
| 30, 1
| 33, 7
| 36, 7
| 43, 8
| |
| 8, 26
| 9, 24
| 10, 85
| 12, 44
| 14, 58
| 16, 27
| 19, 34
| 22, 8
| 25, 0
| 28, 4
| 31, 4
| 35, 0
| 37, 6
| 45, 3
| |
| 8, 90
| 9, 92
| 11, 59
| 13, 24
| 15, 44
| 17, 18
| 20, 3
| 23, 9
| 26, 2
| 29, 6
| 32, 7
| 36, 3
| 38, 9
| 46, 8
| |
| 9, 54
| 10, 60
| 12, 34
| 14, 04
| 16, 31
| 18, 10
| 21, 3
| 24, 9
| 27, 3
| 30, 8
| 33, 9
| 37, 7
| 40, 3
| 48, 3
| |
| 10, 20
| 11, 29
| 13, 09
| 14, 85
| 17, 19
| 19, 02
| 22, 3
| 26, 0
| 28, 4
| 32, 0
| 35, 2
| 39, 0
| 41, 6
| 49, 7
| |
| 10, 86
| 11, 99
| 13, 85
| 15, 66
| 18, 06
| 19, 94
| 23, 3
| 27, 1
| 29, 6
| 33, 2
| 36, 4
| 40, 3
| 43, 0
| 51, 2
| |
| 11, 52
| 12, 70
| 14, 61
| 16, 47
| 18, 94
| 20, 9
| 24, 3
| 28, 2
| 30, 7
| 34, 4
| 37, 7
| 41, 7
| 44, 3
| 52, 6
| |
| 12, 20
| 13, 41
| 15, 38
| 17, 29
| 19, 82
| 21, 8
| 25, 3
| 29, 2
| 31, 8
| 35, 6
| 38, 9
| 42, 9
| 45, 6
| 54, 1
| |
| 12, 88
| 14, 12
| 16, 15
| 18, 11
| 20, 7
| 22, 7
| 26, 3
| 30, 3
| 32, 9
| 36, 7
| 40, 1
| 44, 1
| 47, 0
| 55, 5
| |
| 13, 56
| 14, 85
| 16, 93
| 18, 94
| 21, 6
| 23, 6
| 27, 3
| 31, 4
| 34, 0
| 37, 9
| 41, 3
| 45, 4
| 48, 3
| 56, 9
| |
| 14, 26
| 15, 57
| 17, 71
| 19, 77
| 22, 5
| 24, 6
| 28, 3
| 32, 5
| 35, 1
| 39, 1
| 42, 6
| 46, 7
| 49, 6
| 58, 3
| |
| 14, 95
| 16, 31
| 18, 49
| 20, 6
| 23, 4
| 25, 5
| 29, 3
| 33, 5
| 36, 2
| 40, 3
| 43, 8
| 48, 0
| 50, 9
| 59, 7
| | | | | | | | | | | | | | | | | |
Популярное:
|

