Классические задачи оптимизации

Безусловная оптимизация

Классическая теория экстремумов функции дает признаки абсолютного и относительного, условного и безусловного максимума (минимума):

В классической теории оптимизации различают необходимые и достаточные условия существования экстремума.

Рассмотрим сначала необходимые условия в случае функции одной переменной.

Рассмотрим функцию двух переменных. Если функция f(x, y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует. Эту точку (х₀, у₀) будем называть критической точкой.

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

- Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если - максимум, если - минимум.

- Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума. В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

Аналогично данные положения можно обобщить для n переменных. Необходимым условием существования экстремума в точке является равенство

Пример

Например, градиент функции будет представлять собой:

К стационарным точкам относятся не только точки относительного (локального) экстремума, но и седловые точки (рис.3).

Рис..3. Стационарные точки

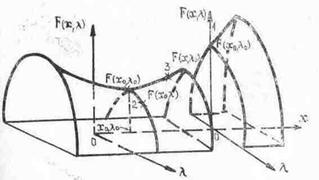
Для W(j₁, j₂) седловая точка – это такая точка j^* =(j₁^*, j₂^*) в которой целевая функция W(j₁, j₂) принимает наименьшее значение по одной координате j₁ и наибольшее значение по другой координате j₂. В окрестности седловой точки для любых значений j₁, j₂всегда выполняется: W(j₁^*, j₂) £ W(j₁^*, j₂^*) £ W(j₁, j₂^*).

На рисунке приведены примеры задачи оптимизации функции двух переменных при отсутствии ограничений.

Достаточным условием существования безусловного относительногоэкстремума функции W(j) является то, чтобы матрица Гессе Н в точке j⁰ ( Н| _j⁰) была либо положительно определенной (тогда j⁰– точка минимума), либо отрицательно определенной (тогда j⁰– точка максимума).

Матрица Гессе Н есть матрица вторых производных W(j). С помощью данной матрицы исследуется знак квадратичной формы , коэффициенты которой определяются соотношениями

Квадратичная форма может быть положительно и отрицательно определенной. Ответ о знаке квадратичной формы дает теорема, которая формулируется следующим образом. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы были выполнены условия Сильвестра – все главные миноры матрицы должны быть строго положительны.

Например, для W(j₁, j₂, j₃)= j₁+2j₃+j₂j₃–j₁²–j₂²–j₃² матрица Гессе Н| _j⁰ имеет вид:

т. к. необходимое условие экстремума Ñ W(j⁰)=0, то

¶W/¶j₁=1–2j₁= 0, ¶W/¶j₁= j₃–2j₂= 0, ¶W/¶j₁= 2+j₂–2j₃= 0.

Для того, чтобы матрица Гессе Н| _j⁰ была положительно определенной (все ее собственные значения были положительны), необходимо и достаточно, чтобы все k-е главные миноры Δ _k матрицы были положительны. Для того, чтобы неособенная квадратная матрица Гессе Н| _j⁰была положительно полуопределенной необходимо и достаточно, чтобы все k-е главные миноры Δ _k матрицы были положительны или равны нулю.

Для того чтобы матрица Гессе Н| _j⁰ была отрицательно определенной (все ее собственные значения были отрицательны), необходимо и достаточно, чтобы k-е главные миноры Δ _k матрицы были отличны от нуля и имеют знак (–1)^k, k=1, 2, …, n. Для того чтобы неособенная квадратная матрица Гессе Н| _j⁰ была отрицательно полуопределенной необходимо и достаточно, чтобы k-е главные миноры Δ _k матрицы были равны нулю или имели знак (–1)^k, k=1, 2, …, n.

Во всех остальных случаях, когда знаки главных миноров не удовлетворяют комбинациям, описанным выше, матрица Гессе Н| _j⁰ является неопределенной.

Главным минором Δ _k неособенной квадратной матрицы называется определитель, образованный элементами, стоящими на пересечении k выделенных строк матрицы и k выделенных столбцов матрицы, причем номера выделенных строк и столбцов матрицы совпадают.

Так, в нашем примере Δ 1 и Δ 3 – отрицательны, Δ 2 - положительный:

Δ 1=a11=–2; Δ 2=

Δ 3=

Таким образом, матрица отрицательно определена.

Условная оптимизация

В классической теории экстремумов рассматриваются задачи математической оптимизации без ограничений. Однако такие задачи имеют чисто теоретическое значение. Это понятно из физической интерпретации целевой функции и ограничений. Т. к. оптимизационные задачи имеют истоки из экономики, то иногда целевую функцию называют функцией дохода, а балансовые уравнения – ресурсными ограничениями. В силу того, что любые практические задачи решаются в условиях ограниченности ресурсов, то становится понятным, что они относятся к задачам нахождения условного экстремума.

Для изучения этих свойств дадим некоторые понятия, связанные со свойствами функций и областями определения их аргументов.

Отрезком, соединяющим две точки F₁ и F₂, называется множество точек с координатами j_i=aj_i₁ + (1–а)j_i₂, (0£ а £ 1, i = ), где j_i₁, j_i₂ – координаты точек F₁ и F₂соответственно; а – изменяемый параметр, определяющий положение точки F на отрезке. Если а=1, то точка F совпадает с точкой F₁, а если а=0, то точка F совпадает с точкой F₂.

Произвольная область называется выпуклой, если вместе с двумя любыми точками она содержит и весь отрезок, соединяющий эти точки.

Определение. Множество называется выпуклым, если для любых выполняется

то есть вместе с любыми двумя точками а и b оно содержит все точки соединяющего их отрезка .

Определение. Функция , заданная на выпуклом множестве , называется выпуклой (вогнутой) на А, если для любых двух точек и Î А выполняется условие

Замечание. В частном случае , когда (как следует из определения, отрезок всегда выпуклое множество), понятие выпуклости (вогнутости) функции одной переменной допускает наглядную геометрическую иллюстрацию. На рис. приведена выпуклая функция ( ).

Пример. В качестве целевой функции принята вероятность решения задачи где u – потенциал решения. Проверить, является ли принятая функция вогнутой.

Решение Вычислим первую и вторую производные функции , получим: , следовательно, функция является вогнутой.

Ответ. Да.

Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (вогнута).

Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется вогнутой, а кривая, обращенная выпуклостью вниз – называется выпуклой.

На рисунке показана иллюстрация приведенного выше определения.

Теорема Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (вогнутая).

Область называется замкнутым полупространством, если ее множество точек удовлетворяет неравенству вида:

а₁j₁+а₂j₂+…+ а_nj_n£ b,

где j_i – оценки альтернатив по i-му критерию (i-я координата вектора свойств альтернатив); а_i – коэффициенты, позволяющие приводить значения j_I к одной шкале. Данное полупространство обладает свойством выпуклости.

Точка F, принадлежащая выпуклой области, называется крайней, если в данной области нет других двух точек F₁ и F₂, что j_i=aj_i₁ + (1–а)j_i₂ таких, что F лежит на этом отрезке. Крайняя точка области не может находиться на отрезке между двумя точками, принадлежащими той же области.

На рис. приведены геометрические иллюстрации сделанных определений.

Фундаментальная теорема математического программирования –теорема Вейерштрасса –формулирует условия существования глобального максимума.

Необходимое условие существования условного относительного экстремума аналогично условию существования безусловного относительного экстремума. Об условном экстремуме говорят, когда целевая функция W(j) ограничена областью F (j Î F) возможных векторов.

Область F задается равенствами или неравенствами функций g_j(j){£, =, ³ }b_j и областью определения (допустимых значений) j_iÎ Q_i, для i = . В данной ситуации внутри области F может не оказаться точки j⁰с координатами (j₁⁰,..., j_n⁰), в которой, градиент функцииW(j) обращается в ноль в ее e - окрестности; либо таких точек может оказаться несколько. Однако, значения W(j) в крайних точках области F могут быть наибольшими (наименьшими), даже больше (меньше), чем в точках относительного экстремума.

Таким образом, условный относительный экстремум может находиться в одной или нескольких точках безусловного относительного экстремума j⁰Î F, (если они есть) либо в одной или нескольких крайних точек.

Отметим, что условие Ñ W(j) = 0 является необходимым, но не достаточным условием существования относительногоэкстремума. Он определяет стационарные точки функции.

Теорема Вейерштрасса. Путь допустимое множество является компактным (т.е. ограниченным и замкнутым) и непустым. Тогда непрерывная целевая функция , определенная на этом множестве, достигает глобального максимума на внутренней или граничной точке этого множества. Геометрическая интерпретация данной теоремы для одномерного вектора приведена на рис. В этом случае вектор сводится к действительному числу. Допустимое множество представляет собой интервал на числовой оси.

Примером одномерной задачи, не имеющей решения, может служить задачи нахождения максимума функции Здесь решения нет, т.к. целевая функция возрастает с увеличением , а верхнего предела нет, т.к., аргумент не ограничен. Надо отметить, что условия теоремы достаточны, а не необходимы. Например, задача максимизации функции имеет решение, хотя допустимое множество не является компактным.

Второй, основной теоремой математического программирования является локально-глобальная теорема, дающая условия, при которых локальный максимум является глобальным.

Теорема (локально-глобальная). Пусть допустимое множество не пусто и является компактным и выпуклым, а непрерывная целевая функция является вогнутой на . Тогда:

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒