Вопрос 2.9.Затухающие колебания.

⇐ ПредыдущаяСтр 3 из 3

Колебания, которые происходят только под действием внутренних сил и при отсутствии сил трения называется собственными колебаниями системы. К ним относятся колебания пружинного и математического маятников. В дальнейшем частоты и периоды собственных колебаний будем обозначать индексом (₀): . Направление уравнение гармонического аксцелятора записывается в виде (1). В реальных системах всегда присутствуют силы трения и сопротивления, поэтому колебания таких систем является затухающим, часть механической энергии тратится на работу против сил трения, поэтому амплитуда колебаний с течением времени уменьшается. При не очень больших скоростях движения сила трения пропорциональна скорости движения. R- коэффициент трения. С учетом силы трения II закон ньютона запишется в виде 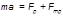(3). -равнодействующая внутренних сил системы. Т.к. 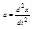, а , то из (2) следует ; . Или (4) – дифференциальное уравнение затухающих колебаний. Обозначим: -коэффициент затухания. . Поэтому: (5)-канонический вид уравнения затухающих колебаний.Решение уравнения (5) имеет вид: 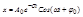(6)- алгебраическое уравнение затухающих колебаний. -амплитуда затухающих колебаний. A₀ – начальная амплитуда. 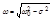(7)-циклическая частота затухающих колебаний.

График затухающих колебаний.

Затухающие колебания уже не являются периодическими в прямом смысле. Хотя система в положение равновесие возвращается через равные промежутки времени. Но через этот промежуток времени, называемый периодом затухающих колебаний значения х не повторяются. Временем релаксации называется время за которое амплитуда колебаний уменьшается в е раз. Из определения вытекает, что . Или , отсюда 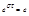, 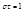; 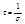(8) – время релаксации. Отношение амплитуды в данный момент времени к амплитуде через период колебания называется декрементом затухания. ; (9) Натуральный логарифм от декремента затухания называется логарифмическим декрементом затухания (10) – Логарифмический декремент затухания.

Вопрос 2.10.Вынужденные колебания.

Чтобы колебания реальных систем были не затухающими на систему необходимо воздействовать переменной внешней силы, которая будет компенсировать потери механической энергии на работу сил трения. Пусть переменная внешней силы изменяется по закону 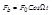(1) - вынужденная сила. Здесь F₀ – амплитуда вынуждающей силы, 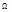- циклическая частота вынужденных сил. В этом случае II закон Ньютона запишется в виде 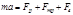(2). С учетом: ; . Из (2) следует или (4)-дифференциальное уравнение вынужденных колебаний. В каноническом виде: (5). Уравнение (5) является неоднородным дифференциальным уравнением II порядка. Решение неоднородного уравнения ищут в виде суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. При вынужденных колебаниях общее решение однородного уравнения (особенности собственных колебаний системы сказывается только в самый начальный период колебания). В установившемся режиме колебаний характер колебаний полностью определяется вынуждающей силой, поэтому решение уравнения (5) будет совпадать с частным решением уравнения (5): (6) – алгебраическое уравнение вынуждающих колебаний. Здесь: (7) – амплитуда вынужденных колебаний. (8)- соотношение для начальной фазы вынужденных колебаний. Как видно из (7) амплитуда вынужденных колебаний является функцией частот вынуждающей силы 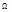и коэффициента затухания

График изменения амплитуды вынуждающих колебаний в зависимости от 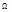и .

Как видно из графика при не котором значении частоты вынуждающей силы амплитуда колебаний резко возрастает. Это является называется явлением резонанса. Частота, при которой происходит резонанс называется резонансной частотой. (9) – резонансная частота. Как видно из графика, чем меньше коэффициент затухания, тем больше амплитуда при резонансе и тем острее пик графика. Из (9) видно, что если , то -резонансная частота, т.е. резонанс достигается, когда частота вынуждающей силы приближается к собственной частоте вынуждающей силы.

⇐ Предыдущая 1 23