Анализ одноканальной системы массового обслуживания с ожиданием.

Рис.4.3. Схема одноканальной СМО с ожиданием.

Рис.4.4. Граф состояний одноканальной разомкнутой СМО.

P₀, P_1,…, P_n вероятности наличия 0, 1, 2…n требований в системе.

Система уравнений:

……………… (4.10)

…………………

В стационарном режиме: , n=0, 1, …

-P₀l+P₁m=0

P₀l-(l+m)P₁+P₂m=0 (4.11)

……………………

P_n-1l-(l+m)P_n+P_n+1m=0

……………………

Выразим вероятности состояний системы в виде некоторой реккурентной формулы.

Из первого уравнения системы (2) определяем наличие одного требования в системе:

где (коэффициент использования).

Из второго уравнения – вероятность наличия двух требований в системе:

, где или:

Вероятность наличия в СМО 3-х требований:

Суммируя полученные значения для P₀, P_1,…, P_n находим:

Используя формулу суммы геометрической прогрессии, получаем:

При n®¥ , откуда имеем вероятность простоя канала обслуживания: (4.12)

Вероятность того, что в системе находится n требований:

(4.13)

Можно получить следующие формулы:

Среднее число требований находящихся в системе: (4.14)

Среднее число требований находящихся в очереди: (4.15)

Среднее время ожидания требования в системе: (4.16)

Анализ одноканальной замкнутой системы с ожиданием.

Рис.4.5. Граф состояний системы.

m – число требований нуждающихся в обслуживании; l - интенсивность поступления одного требования.

Основные формулы:

Вероятность того, что в системе находится n требований: (4.17)

Вероятность простоя канала обслуживания: (4.18)

Среднее число требований, находящихся в очереди: (4.19)

Среднее время ожидания требования в очереди: (4.20)

Среднее время ожидания требования в системе: (4.21)

Анализ многоканальной разомкнутой системы с отказом.

Рис.4.6. Граф состояний системы.

Интенсивность поступления требований в систему l; N – количество каналов. Если N каналов занято, то требование получает отказ и покидает систему. Задача решена датским учёным Эрлангом.

Возможные состояния системы:

P₀– все каналы свободны, ни одно требование не обслуживается;

P₁– один канал занят, обслуживается одна заявка;

…………………………………………………

Р_n– каналов занято, обслуживается n требований;

P_{N –} все N каналов заняты, обслуживается N требований;

(4.22)

Из первого уравнения: ; из второго уравнения с учётом первого равенства

(4.23)

Используя полученные соотношения, определим вероятность P₀ того, что все каналы обслуживания свободны: Þ (4.24)

Вероятность того, что занято ровно n каналов обслуживания: (4.25)

Среднее число занятых каналов обслуживания: (4.26)

Анализ многоканальной замкнутой системы с ожиданием.

Рис.4.6. Граф состояний системы.

n – число требований поступивших в систему; N – число каналов обслуживания; m –число требований нуждающихся в обслуживании; N£ n£ m.

Возможно 2 случая:

1) Число требований n, поступивших в систему меньше числа каналов обслуживания,

т.е они все находятся на обслуживании. 0£ n£ N

2) Число требований n, поступивших в систему больше или равно числу каналов

обслуживания n³ N из них N обслуживаются, а z требований ожидают в очереди

(z=1, 2, …, m-N).

Вероятность того, что в системе находится n требований:

для 0£ n£ N (4.27)

для N£ n£ m (4.28)

Пример анализа стационарного режима работы системы массового обслуживания.

Двухпроцессорная информационно-управляющая система управляет работой шести технологических установок. Каждая установка требует управляющего воздействия в среднем каждые30 секунд. Процесс решения задачи управления и выдачи управляющего воздействия занимает 10 с. Определить среднюю загрузку процессоров т. е. среднее число работающих процессоров, абсолютную пропускную способность такой системы и среднюю производительность технологического комплекса из шести установок, если производительность одной установки составляет 120 т/час, а при неудовлетворении системой заявки на решение задачи управления установка переходит на холостой режим работы и продукцию не выпускает.

Функциональная схема системы имеет вид:

Рис. 4.7. Функциональная схема системы

Обозначения на рис. 4.7.

П1, П2 – процессоры; ИУС - информационно-управляющая система; 1¸ 6 – технологические установки; ош- общая шина;

Граф состояний системы имеет вид:

Рис. 4.8 Граф системы.

Обозначения: S₀¸ S₆ – состояния системы; P₀¸ P₆ – вероятности состояний системы; – интенсивность входного потока требований, создаваемого одной установкой, ; m - интенсивность выходного потока требований, создаваемого одним процессором^*, .

Таблица состояний системы 4.1 строится по графу рис. 4.8.

Таблица 4.1

S	S₀	S₁	S₂	S₃	S₄	S₅	S₆
P	P₀	P₁	P₂	P₃	P₄	P₅	P₆
Nрп
Nру
Nну

Обозначения в таблице 4.1:

Nрп – число работающих процессоров;

Nру – число работающих технологических установок;

Nну – число неработающих технологических установок;

Система уравнений вероятностей состояний, составленная по графу рис. 4.8. будет иметь вид:

(4.29)

P₀+P₁+P₂+P₃+P₄+P₅+P₆=1

Последнее уравнение системы (4.29) называют нормализующим. Оно является обязательным при исследовании стационарного режима работы системы массового обслуживания.

Решим систему уравнений (4.29) методом подстановки:

Откуда: ; Р₁=0, 306; Р₂=0, 255; Р₃=0, 17; Р₄=0, 085; Р₅=0, 02; Р6=0, 00459

Число работающих процессоров является дискретной случайной величиной, поэтому среднее число работающих процессоров рассчитывается по формуле математического ожидания:

M(Nрп)=1Р₁+2Р₂+2Р₃+2Р₄+2Р₅+2Р₆=1, 388

Абсолютная пропускная способность системы:

Q=M(N_рп)m=1, 388·6=8, 328

Средняя производительность технологического комплекса из шести установок:

Q=qM(Nру),

где: q= - производительность одной технологической установки; M(Nру) – матаматическое ожидание числа работающих установок.

M(Nру)= 6Р₀+5Р₁+4Р₂+3Р₃+2Р₄+1Р₅=6·0, 153+5·0, 306+4·0, 255+3·0, 17+2·0, 085+1·0, 02=

=4, 168 (установок)

Q=120·4, 168=500, 16(т/час)

*Примечание . На параметр m в данном случае влияют: быстродействие процессоров, объем оперативной памяти, функционально-алгоритмическая структура системы управления и т.д.На параметр l влияют: типы и характеристики технологического оборудования, режимы работы оборудования, характеристики возмущающих воздействий.

При системном анализе выбирают такое соотношение между этими параметрами, чтобы производительность комплекса была максимальной.

Пример анализа надежности системы.

Под надежностью понимают вероятность объекта или процесса полностью выполнять возложенные на него функции. Различают системы с восстановлением т.е. с ремонтом и обслуживанием и системы без восстановления. Граф системы без восстановления имеет вид:

Рис. 4.9 Граф системы без восстановления

Обозначения: S1 - состояние работоспособности системы; S2 - состояние отказа системы; P1 - надежность системы; P2 -вероятность отказа системы; l - интенсивность отказа системы^*.

Уравнения вероятностей состояния по графу рис.4.9 будут иметь вид:

(4.30)

Откуда:

(4.31)

Рис.4.10. Графики надежности системы без восстановления.

Время наработки на отказ .

Граф системы с восстановлением будет иметь вид:

Рис. 4.10. Граф системы с восстановлением.

Система уравнений Колмогорова:

(4.32)

В операторной форме система (4.32.) записывается в виде:

zP₁(z)+lP₁(z)-mP₂(z)=1

zP₂(z)+mP₂(z)-lP₁(z)=0

где z – оператор Лапласа;

Изображение производных получено по правилу

zP(z)-P(0),

где Р(0) значение вероятностей при t=0. В данном случае Р₁(0)=1; Р₂(0)=0.

Из 2-го уравнения системы (4.34)

(4.34)

Подставим Р₂(z) из (4.34) в первое уравнение системы (4.33), получим:

(4.35)

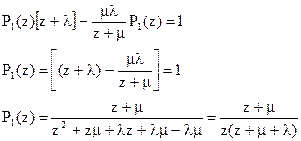
Умножим и разделим правую часть P₁(z) на постоянную величину равную (l +m)

Используем таблицу оригиналов и изображений:

Оригинал решения системы дифференциальных уравнений (4.32) будет:

Рис. 4.11 Графики надежности:

1 – система без восстановления;

2 – система с восстановлением;

– коэффициент готовности системы.

*Примечания Величина находится по правилам последовательного и параллельного соединения элементов в системе.

При последовательном соединении отказ одного элемента приводит к отказу всей системы.

Интенсивность отказов в системе l находится по формуле:

, (4.36)

где l_i – интенсивность отказа i -го элемента; N - число элементов в системе.

Надежность системы без восстановления при последовательном соединении элементов:

, (4.37)

где Р_i - вероятность безотказной работы i -го элемента

Формула (4.36) может быть получена из формулы (4.37)

(4.38)

(4.39)

Паралленым называется соединение элементов с резервированием, когда отказ элемента не приводит к отказу всей системы.

При параллельном соединении злементов, вероятность отказа системы:

, (4.40)

где Q_i - вероятность отказа i -го элемента; N - число параллельно соединенных элементов.

Вероятность безотказной работы или надежность системы из N-параллельно соединенных элементов.

(4.41)

Анализ формул (4.37) и (4.41) показывает, что с возрастанием числа N последовательно соединенных элементов надежность системы уменьшается, а с возрастанием числа N параллельно соединенных элементов надежность системы увеличивается.

⇐ Предыдущая 1 2 3 4 567 8 9 Следующая ⇒