Допущения, на которых базируется дисперсионный анализ

Наблюдения переменной Y - есть нормально распределенные случайные величины с математическим ожиданием M[Y]=m_y. Дисперсия единичного наблюдения обусловлена случайными ошибками ε, постоянна во всех опытах и на всех уровнях факторов x_i .

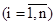Идея дисперсионного анализа

Чтобы иметь возможность оценивать влияние каждого фактора на переменную Y и сравнивать влияние различных факторов следует установить некоторый количественный показатель этого влияния. Рассмотрим идею дисперсионного анализа на примере изучения влияния одного фактора X на m уровнях, получим значения отклика y₁, y₂, …, y_n, рассеяние которых можно характеризовать выборочной дисперсией 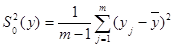, где . Число степеней свободы есть ν ₀=m-1. Если отличие от незначимо, то разброс наблюдений, который она характеризует, связан только со случайными причинами и влияние фактора X несущественно. Если же отличие от значительно, то повышенный разброс наблюдений вызывается не только случайными причинами, но и влиянием фактора X, которое следует признать существенным.

Так как в последнем случае складывается влияние по крайней мере двух факторов: 1) случайных причин с дисперсией ; 2) фактора X с дисперсией , что приводит к общему рассеянию наблюдений, то их общая дисперсия является суммой , а ее оценка:

Откуда дисперсия фактора X определяется выражением:

В общем случае дисперсия ошибок неизвестна, поэтому схема дисперсионного анализа должна быть такой, чтобы позволяла определить ее наряду с оценкой дисперсии фактора X. С этой целью планируется проведение серии параллельных опытов на каждом из всех возможных сочетаний уровней факторов. Таким образом, основная идея дисперсионного анализа заключается в разложении оценки общего рассеяния на составляющие, зависящие от: 1) случайных причин; 2) от каждого из рассматриваемых факторов.

Алгоритм решения задачи

Рассмотрим процедуру однофакторного дисперсионного анализа. Пусть фактор X варьируется на n уровнях. Результаты можно представить в виде следующей таблицы:

			…	p
	y₁₁	y₁₂	…	y₁_p
	y₂₁	y₂₂	…	y₂_p
…	…	…	…	…	…
N	y_n1	y_n2	…	y_np

Не нарушая общности выводов, рассмотрим случай равночисленных серий наблюдений на всех уровнях , т.е p_i=p.

Рассеяние между столбцами обусловлено ошибкой воспроизводимости, а рассеяние между строчками – действием изучаемого фактора X. Вычислим среднее арифметическое серий из p наблюдений для каждого i-го уровня фактора с помощью соотношения вида:

(1)

Общее среднее арифметическое всех n× p наблюдений по всем уравнениям вычисляется следующим образом:

(2)

Рассеяние отдельных наблюдений относительно общего среднего обусловлено действием как случайных причин, так и влиянием фактора X. Действие фактора случайности проявляется в рассеянии (с дисперсией ) наблюдений серий параллельных исследований на каждом уровне x_i вокруг среднего арифметического своей серии. Влияние же фактора X (с дисперсией ) вызывает повышенное рассеяние средних арифметических относительно общего среднего . Каждое из этих трех рассеяний можно охарактеризовать соответствующей суммой квадратов отклонений. В соответствии с основной идеей дисперсионного анализа разложим общую сумму квадратов отклонений y_ij от общего среднего на две составляющие, одна из которых характеризует влияние фактора случайности, а другая – фактора изменчивости:

(3)

Оценки дисперсий: Предположим, что влияние фактора Х на отклик отсутствует, т.е. гипотеза Н₀ об однородности , верна. Тогда все n серий параллельных наблюдений можно рассматривать как случайные выборки одной и той же генеральной совокупности и, следовательно:

1) Несмещенная общая оценка дисперсии воспроизводимости по всем n× p наблюдениям определяется выражением:

(4)

с числом степеней свободы ;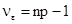

2) выборочная дисперсия рассеивания «внутри серий» или остаточная оценка дисперсии воспроизводимости , находится как среднее из выборочных дисперсии по каждой серии в отдельности:

(5)

с числом степеней свободы ;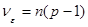

3) выборочная дисперсия средних по сериям служит несмещенной оценкой дисперсии с которой нормально распределены независимые друг от друга средние i-ых серий:

(6)

с числом степеней свободы . Отсюда нетрудно получить третью оценку воспроизводимости, выборочную дисперсию рассеивания «между сериями»:

(7)

с числом степеней свободы . Подсчет чисел степеней свободы проверяется с помощью соотношения .

Из сказанного очевидно, что при отсутствии влияния фактора Х оценки однородны, так как являются оценками одной и той же генеральной дисперсии.

Предположим теперь, что влияние фактора Х на отклик существенно, т.е. гипотеза Н₀ об однородности , неверна. Тогда n серий наблюдений можно рассматривать как случайные выборки независимых нормально распределенных случайных величин с одной и той же дисперсией воспроизводимости и различными генеральными средними m₁, m₂, …, m_n и, следовательно:

1) выборочная дисперсия характеризует влияние как фактора случайности ε, так и фактора Х, т.е. ;

2) так как сумма не изменяется при замене y_ij на y_ij-m_i, то выборочная дисперсия также не изменяется и по-прежнему является несмещенной оценкой для генеральной дисперсии воспроизводимости , т.е. ;

3) поскольку сумма учитывает не только случайные, но и систематические расхождения между средними серий и увеличивается за счет влияния фактора Х, дисперсия при этом также увеличивается и перестает служить оценкой только , откуда следует, что .

Из сделанного второго предположения очевидно, что при влиянии фактора Х оценки неоднородны. Следовательно, сопоставляя эти выборочные дисперсии, можно принять решение о справедливости первого или второго предположения относительно существенности влияния фактора Х (с дисперсией ) на отклик.

Оценка влияния фактора. Для того, чтобы влияние фактора Х было признано существенным ( > 0), необходимо и достаточно, чтобы оценка дисперсии значимо отличалось от . Проверку исходной гипотезы Н₀ об однородности этих выборочных дисперсии можно осуществить с помощью критерия Фишера:

(8)

При использовании критерия Фишера применяется следующее правило принятие решения: Если , то влияние фактора Х признается существенным, и, наоборот, если , то влияние фактора Х признается несущественным.

Содержание отчета

1. Описание процедуры дисперсионного анализа, с указанием соотношений (1)-(8).

2. Результаты решения каждой из трех задач в виде:

вычисленные средние по каждой серии ( );

общее среднее ( );

оценка дисперсии рассеивания «между сериями»;

оценка дисперсии рассеивания «внутри серии»;

значение критерия Фишера (Fn);

результат анализа: зависит или нет процесс от фактора.

ТЕОРИЯ К ЗАДАЧЕ №2

123	Поделиться: