Сложение и равновесие пар сил на плоскости

Сложение пар производится алгебраическим суммированием их моментов:

М = М₁ + М₂ + …+ М_n = Σ М_i

 

Условие равновесия системы пар, лежащих в одной пло­скости: для равновесия системы пар необходимо чтобы сумма моментов пар равнялась нулю:

Σ М_i = 0 (3.2)

Пример 3.1. Определить момент результирующей пары, эквивалентной системе трех пар, лежащих в одной плоскости (рис. 3.3). Первая пара F₁ = F¢ ₁ = 2 кН, плечо h₁ = 1, 25 м; вторая пара F_{2 =} F¢ ₂ = 3 кН, плечо h ₂ = 2 м; третья пара F₃ = F¢ ₃ = 4, 5 кН, плечо h₃ = 1, 2 м.

 

Рис. 3.3

Момент силы относительно точки

 

Момент М_о (F)силы F относительно точки О равен произведению силы на плечо. (рис. 3.4, а). Сила F стремится поворачи­вать плечо а вокруг точки О.

М_о (F) = F× a, Н× м, (3.3)

где а - плечо силы F.

Плечо силы – этодлина перпенди­куляра а, опущенного из точки на линию действия силы

Рис. 3.4

 

Центр момента - точка О, относительно которой возникает момент.

 

Момент по­ложительный, если сила стре­мится вращать тело по часовой стрелке (рис. 3.4, а), и отри­цательный — против часовой стрелки (рис. 3.4, б).

 

Когда линия действия силы проходит через данную точку, момент силы относительно этой точ­ки равен нулю, так как плечо а = 0 (рис. 3.4, в).

 

Лекция № 4

ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ

Опорные устройства балочных систем

 

1) Шарнирно-подвижная опора (рис. 4.1, а)- допускает поворот вокруг оси шарнира и линейное перемещение па­раллельно опорной плоскости. Направление опорной реакции - перпендикуляр к опорной плоскости. (рис. 5.1, б).

2) Шарнирно-неподвижная опора (рис, 4.1, б) - допу­скает только поворот вокруг оси шарнира, но не допускает никаких ли­нейных перемещений. Опорная реакция R_A раскладывается на две составляющие - R_Ax и R_Ay.

3) Жесткая заделка (защемление) (рис. 4.1, в)- не допускает ни линейных перемещений, ни поворота.В защемлении действуют две составляющие опорной реакции - R_Ax, R_Ay и реактивный момент М_А.

а) б) в)

Рис. 4.1

Двухопорные балки имеют две опоры – одна опора шарнирно-неподвижная, вторая – шарнирно-подвижная. Шарнирно-подвижная опора необходима для компенсации перемещений балки при температурных расширениях балки из-за колебаний температуры, а также при возможной подвижке опоры, например, при осадке почвы.

Виды балок

Консоль – выступающая за опору не закрепленная часть балки (рис. 4.2, б, в).

1) Бесконсольные балки 2) Одноконсольные балки 3) Двухконсольные балки

 

	консоль

а) б) в)

Рис. 4.2

Виды нагрузок

 

1) Сосредоточенная сила (рис.4.3, а) – F - сила, приложенная в одной точке.

а) б) в)

Рис. 4.3

2) Равномерно распределенная нагрузка (рис.4.3, б) – нагрузка, равномерно распределенная на некоторой длине l . Характеризуется интенсивностью q, единица измерения - Н/м или кН/м.

При решении задач равномерно распределенная нагрузка интенсивностью q заменяется одной силой F_q = q× l , которая является равнодействующей силой и прикладывается посередине длины l .

 

3) Пара сил или момент (рис. 4.3, в) – М, Н× м.

 

Равновесие плоской системы сил

 

Условие равновесия произвольной плоской системы сил - произвольная плоская система сил находится в равно­весии, когда алгебраические суммы проекций сил на координатные оси и сумма моментов равны нулю:

Первый вид: Второй вид: Третий вид:

 

SF_ix = 0 S F_ix = 0 SМ_А = 0

SF_iу = 0 SМ_А = 0 SМ_В = 0

SМ_о = 0 SМ_В = 0 SМ_С = 0

Решение задач на определение опорных реакций

 

Для решения задач надо составить столько уравнений равновесия, сколько неизвестных сил в задаче. Для определения опорных реакций двухопорной балки (R_Ax, R_Ay и R_В) необходимо составить три уравнения равновесия второго вида: SF_ix = 0, SМ_А = 0, SМ_В = 0.

 

Пример 4.1 . Определить опорные реакции балки, изображенной на рис. 4.4, а, нагруженной парой с моментом М = 10 кН× м, сосредоточенной силой F = 4 кН и распределенной нагрузкой интенсивностью q = 1, 5 кН/м.

Решение.

1) Чертим расчетную схему (рис. 4.5). На расчетной схеме заменяем распределенную нагрузку q ее рав­нодействующей F_q = q× b, которая прикладывается посредине нагруженного участка b. Освобождаем балку от опор, а их действие заменяем реакциями - R_Aу, R_Ax и Rb. Проставляем расстояния между всеми силами и моментами – a, c, d, а также общую длину балки – l.

 

	2) Составляем уравнения равновесия: SFlx = 0 RAx = 0; SМА = 0 -M + qb(а + с) + F× l - RB l =0. SМВ = 0 - qb× d - М + RAyl = 0; 3) Решаем уравнения: Rb = = = 8, 37 кН RАy = =4, 62кН

а)

б)

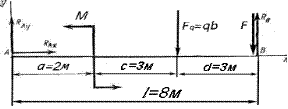
Рис. 4.4 Расчетная схема

 

4) Проверяем найденные значения реакций :

 

SF_iv = 0; R_Ay - qb +R_B - F = 4, 63 – 1, 5× 6 + 8, 37 - 4 = 0. Реакции найдены верно.

 

Лекция № 5

ЦЕНТР ТЯЖЕСТИ

12	Поделиться:

Популярное:

1. Case-study использования шпаргалок в Москве
2. Gigabit Ethernet на витой паре категории 5
3. I. 17. Понятие о чистых и занятых парах.
4. I. Основные физические явления и процессы в электрических аппаратах
5. II. Страх. Второй текст: 1 Паралипоменон 13,12.
6. III Часть. Аппаратное обеспечение обработки информации
7. III. 5. СЛОВА-ПАРОНИМЫ И ТОЧНОСТЬ РЕЧИ
8. Il est de Paris. Он – из Парижа.
9. А потом он спросил меня о том, как мы живём, и я рассказала ему, что мы
10. А хочу лишь исправить то, что в моих силах. Помогает мне только Аллах.
11. АВТОМАТИЗАЦИЯ СУДОВЫХ ПАРОВЫХ КОТЛОВ
12. АДП (Агрегат депарафинизации)