Значения функции плотности вероятности нормированного
нормального распределения 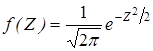

|
|
|
|
|
|
|
|
|
|
| | 0, 0
| 0, 3989
|
|
|
|
|
|
|
|
|
| | 0, 1
|
|
|
|
|
|
|
|
|
|
| | 0, 2
|
|
|
|
|
|
|
|
|
|
| | 0, 3
|
|
|
|
|
|
|
|
|
|
| | 0, 4
|
|
|
|
|
|
|
|
|
|
| | 0, 5
|
|
|
|
|
|
|
|
|
|
| | 0, 6
|
|
|
|
|
|
|
|
|
|
| | 0, 7
|
|
|
|
|
|
|
|
|
|
| | 0, 8
|
|
|
|
|
|
|
|
|
|
| | 0, 9
|
|
|
|
|
|
|
|
|
|
| | 1, 0
| 0, 2420
|
|
|
|
|
|
|
|
|
| | 1, 1
|
|
|
|
|
|
|
|
|
|
| | 1, 2
|
|
|
|
|
|
|
|
|
|
| | 1, 3
|
|
|
|
|
|
|
|
|
|
| | 1, 4
|
|
|
|
|
|
|
|
|
|
| | 1, 5
|
|
|
|
|
|
|
|
|
|
| | 1, 6
|
|
|
|
|
|
|
|
|
|
| | 1, 7
|
|
|
|
|
|
|
|
|
|
| | 1, 8
|
|
|
|
|
|
|
|
|
|
| | 1, 9
|
|
|
|
|
|
|
|
|
|
| | 2, 0
| 0, 0540
|
|
|
|
|
|
|
|
|
| | 2, 1
|
|
|
|
|
|
|
|
|
|
| | 2, 2
|
|
|
|
|
|
|
|
|
|
| | 2, 3
|
|
|
|
|
|
|
|
|
|
| | 2, 4
|
|
|
|
|
|
|
|
|
|
| | 2, 5
|
|
|
|
|
|
|
|
|
|
| | 2, 6
|
|
|
|
|
|
|
|
|
|
| | 2, 7
|
|
|
|
|
|
|
|
|
|
| | 2, 8
|
|
|
|
|
|
|
|
|
|
| | 2, 9
|
|
|
|
|
|
|
|
|
|
| | 3, 0
| 0, 0044
|
|
|
|
|
|
|
|
|
| | 3, 1
|
|
|
|
|
|
|
|
|
|
| | 3, 2
|
|
|
|
|
|
|
|
|
|
| | 3, 3
|
|
|
|
|
|
|
|
|
|
| | 3, 4
|
|
|
|
|
|
|
|
|
|
| | 3, 5
|
|
|
|
|
|
|
|
|
|
| | 3, 6
|
|
|
|
|
|
|
|
|
|
| | 3, 7
|
|
|
|
|
|
|
|
|
|
| | 3, 8
|
|
|
|
|
|
|
|
|
|
| | 3, 9
|
|
|
|
|
|
|
|
|
|
| 5) Задаются уровнем значимости q. Значение q выбирают из диапазона  . .
6) По таблице Пирсона (табл. 3.11) находят теоретическое значение  , где , где  – доверительная вероятность. – доверительная вероятность.
7) Сравнивают  и и  и делают вывод. Если и делают вывод. Если  - гипотеза о нормальности отвергается; если - гипотеза о нормальности отвергается; если  – нет оснований отвергать гипотезу о нормальности. – нет оснований отвергать гипотезу о нормальности.
Таблица 3.11
Критические значения  при доверительной при доверительной
вероятности Р и числе степеней свободы L' – 3
| Число степеней свободы L' – 3
| Доверительная вероятность Р
| | 0, 80
| 0, 90
| 0, 95
| 0, 98
| 0, 99
| 0, 999
| |
| 5, 99
| 7, 78
| 9, 49
| 11, 67
| 13, 28
| 18, 5
| |
| 7, 29
| 9, 24
| 11, 07
| 13, 39
| 15, 09
| 20, 5
| |
| 8, 56
| 10, 64
| 12, 59
| 15, 03
| 16, 08
| 22, 5
| |
| 9, 80
| 12, 02
| 14, 07
| 16, 60
| 18, 50
| 24, 30
| |
| 11, 03
| 13, 36
| 15, 51
| 18, 20
| 20, 10
| 26, 1
| |
| 12, 24
| 14, 68
| 16, 90
| 19, 70
| 21, 70
| 27, 9
| |
| 13, 44
| 15, 99
| 18, 30
| 21, 20
| 23, 20
| 29, 6
| |
| 14, 63
| 17, 30
| 19, 70
| 22, 60
| 24, 20
| 31, 30
| |
| 15, 80
| 18, 50
| 21, 00
| 24, 10
| 26, 20
| 32, 9
| |
| 17, 00
| 19, 80
| 22, 40
| 25, 50
| 27, 70
| 34, 5
| |
| 18, 20
| 21, 10
| 23, 70
| 26, 90
| 29, 10
| 36, 1
| |
| 19, 30
| 22, 30
| 25, 00
| 28, 30
| 30, 60
| 37, 7
| |
| 25, 00
| 28, 40
| 31, 40
| 35, 00
| 37, 60
| 45, 3
| |
| 36, 30
| 40, 30
| 43, 80
| 48, 00
| 50, 90
| 59, 7
|
Алгоритм проверки гипотезы о промахах
Промах – неудачный результат наблюдения, который следует исключить. Предположим, что в выборке  значение значение  представляет собой сомнительный результат. Следует решить вопрос: выбросить или оставить в выборке значение представляет собой сомнительный результат. Следует решить вопрос: выбросить или оставить в выборке значение  . Исключение подобного результата из рассмотрения осуществляется с помощью следующего метода: . Исключение подобного результата из рассмотрения осуществляется с помощью следующего метода:
1) предполагается, что гипотеза о нормальном законе непротиворечива;
2) вычисляются среднее арифметическое  и среднее квадратическое отклонение и среднее квадратическое отклонение  выборки без сомнительных результатов; выборки без сомнительных результатов;
3) вычисляется значение
 . (3.87) . (3.87)
Данные для доверительной вероятности и определенного числа результатов (без сомнительных) –  приводятся в табл. 3.12. Если приводятся в табл. 3.12. Если  , то , то  – промах; если – промах; если 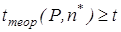 , то нет оснований , то нет оснований  считать промахом. считать промахом.
Таблица 3.12
Критические значения 
| n*
| Доверительная вероятность Р
| n*
| Доверительная вероятность Р
| | 0, 95
| 0, 98
| 0, 99
| 0, 999
| 0, 95
| 0, 98
| 0, 99
| 0, 999
| |
| 3, 04
| 4, 11
| 5, 04
| 9, 43
|
| 2, 145
| 2, 602
| 2, 932
| 3, 979
| |
| 2, 78
| 3, 54
| 4, 36
| 7, 41
|
| 2, 105
| 2, 541
| 2, 825
| 3, 819
| |
| 2, 62
| 3, 36
| 3, 96
| 6, 37
|
| 2, 079
| 2, 503
| 2, 802
| 3, 719
| |
| 2, 51
| 3, 18
| 3, 71
| 5, 73
|
| 2, 061
| 2, 476
| 2, 768
| 3, 652
| |
| 2, 43
| 3, 05
| 3, 54
| 5, 31
|
| 2, 048
| 2, 456
| 2, 742
| 3, 602
| |
| 2, 37
| 2, 96
| 3, 41
| 5, 01
|
| 2, 038
| 2, 441
| 2, 722
| 3, 565
| |
| 2, 33
| 2, 89
| 3, 31
| 4, 79
|
| 2, 030
| 2, 429
| 2, 707
| 3, 532
| |
| 2, 29
| 2, 83
| 3, 23
| 4, 62
|
| 2, 018
| 2, 411
| 2, 683
| 3, 492
| |
| 2, 26
| 2, 78
| 3, 17
| 4, 48
|
| 2, 009
| 2, 399
| 2, 667
| 3, 462
| |
| 2, 24
| 2, 74
| 3, 12
| 4, 37
|
| 2, 003
| 2, 389
| 2, 655
| 3, 439
| |
| 2, 22
| 2, 71
| 3, 08
| 4, 28
|
| 1, 998
| 2, 382
| 2, 646
| 3, 423
| |
| 2, 20
| 2, 63
| 3, 04
| 4, 20
|
| 1, 994
| 2, 377
| 2, 639
| 3, 409
| |
| 2, 18
| 2, 66
| 3, 01
| 4, 13
|
| 1, 960
| 2, 326
| 2, 576
| 3, 291
|
Запись результата измерений
При записи результата измерений предположим, что систематическая составляющая погрешности отсутствует. Тогда за оценку результата измерения следует принять математическое ожидание, т. е.
 . (3.88) . (3.88)
Для определения границ случайной погрешности вычисляется оценка среднего квадратического отклонения среднего арифметического:
 (3.89) (3.89)
где n' – число наблюдений после удаления промахов.
Границы случайной погрешности определяются по выражению:
 , (3.90) , (3.90)
где  – коэффициент Стьюдента (табл. 3.13); – коэффициент Стьюдента (табл. 3.13);
p - заданное значение доверительной вероятности;
 – число степеней свободы. – число степеней свободы.
3.5.2. План выполнения работы
1) Получить у преподавателя вариант исследуемой электрической цепи.
2) Составить схему замещения. Параметры элементов схемы замещения привести в табл. 3.14.
Таблица 3.13
Значение коэффициентов Стьюдента
| Число степеней свободы ν
| Доверительная вероятность Р
| | 0, 9
| 0, 95
| 0, 99
| |
| 6, 31
| 12, 71
| 63, 66
| |
| 2, 92
| 4, 30
| 9, 92
| |
| 2, 53
| 3, 18
| 5, 84
| |
| 2, 13
| 2, 78
| 4, 60
| |
| 2, 02
| 2, 57
| 4, 03
| |
| 1, 94
| 2, 45
| 3, 71
| |
| 1, 90
| 2, 37
| 3, 50
| |
| 1, 86
| 2, 31
| 3, 36
| |
| 1, 83
| 2, 26
| 3, 25
| |
| 1, 81
| 2, 23
| 3, 17
| |
| 1, 78
| 2, 18
| 3, 06
| |
| 1, 76
| 2, 15
| 2, 98
| |
| 1, 75
| 2, 12
| 2, 92
| |
| 1, 73
| 2, 10
| 2, 88
| |
| 1, 73
| 2, 09
| 2, 85
| |
| 1, 72
| 2, 07
| 2, 82
| |
| 1, 71
| 2, 06
| 2, 80
| |
| 1, 71
| 2, 06
| 2, 76
| |
| 1, 70
| 2, 05
| 2, 76
| |
| 1, 70
| 2, 04
| 2, 75
| | ∞
| 1, 64
| 1, 96
| 2, 58
|
Таблица 3.14
Параметры элементов схемы замещения
| Номер элемента
| (R ± DR), Ом
| Rmin, Ом
| Rmax, Ом
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
3) Методом статистических испытаний разыграть по 60 моделей каждого резистора (см. п. 3.5.1.1). Результаты испытаний привести в табл. 3.15.
Таблица 3.15
Результаты статистических испытаний
| Номер испытаний
| Параметры моделей, Ом
| Входное сопротивление Rвх i, Ом
| | R1i
| R2i
| R3i
| R4i
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| | …
|
|
|
|
|
| |
|
|
|
|
|
| |
| 
|
4) Построить эмпирические распределения параметров элементов и входного сопротивления (п. 3.5.1.1).
Результаты обработки статистического ряда для каждого резистора заданной цепи и входного сопротивления свести в табл. 3.16.
Таблица 3.16
Популярное:
|

