Таблицы соотношений коэффициентов четырехполюсников, параметров элементов ЭЭС и параметров П-образной схемы замещения
Таблица П.1
Соотношения коэффициентов четырехполюсников с параметрами ЛЭП, трансформаторов и нагрузки
| Коэффициенты четырехполюсника
| Модель ЛЭП с распределенными параметрами
| Модель идеальной ЛЭП с распределенными параметрами
| Модель ЛЭП без учета распределенности параметров
| Трансформатор (понижающий) n > 1
| Трансформатор (повышающий) n > 1
| Нагрузка
|
| A
| 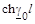
| 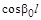
| 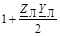
| n
| 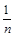
|
|
| B
| 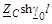
| 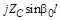
| 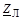
| 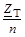
| 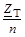
|
|
| C
| 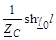
| 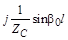
| 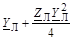
| 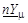
| 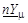
| 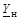
|
| D
| 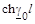
| 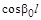
| 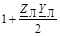
| 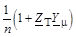
| 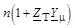
|
|
Таблица П.2
 Соотношения между параметрами П-образных схем замещения и параметрами ЛЭП,
Соотношения между параметрами П-образных схем замещения и параметрами ЛЭП,
трансформаторов и нагрузки
| Параметры П-образной схемы замещения
| Модель ЛЭП с распределенными параметрами
| Модель идеальной ЛЭП с распределенными параметрами
| Модель ЛЭП без учета распре-деленности параметров
| Трансформатор (понижающий)
n > 1
| Трансформатор (повышающий)
n > 1
| Нагрузка
|
| Z
| ZCshg0l
| jZCsinb0l
| (r0 + jx0)l
| 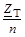
| 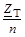
|
|
| Y1
| 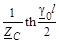
| 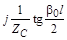
| 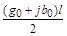
| 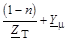
| 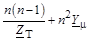
|
|
| Y2
| 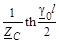
| 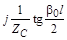
| 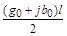
| 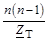
| 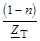
| Yн
|
Оглавление
Предисловие........................................................................................................................ 3
1. МОДЕЛИРОВАНИЕ ПРИ РЕШЕНИИ ИНЖЕНЕРНЫХ ЗАДАЧ....................... 5
1.1. Решение задач и моделирование.................................................................... 5
1.2. Классификация моделей................................................................................... 7
1.3. Переменные в математических моделях.................................................... 10
1.4. Адекватность и эффективность математических моделей.................. 15
1.5. Свойства объектов моделирования............................................................. 18
1.6. Математические модели на микроуровне................................................. 22
1.7. Моделирование на макроуровне................................................................. 25
1.8. Моделирование на метауровне.................................................................... 29
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЭЛЕМЕНТОВ ЭЭС...................................... 32
2.1. Линия электропередачи.................................................................................. 32
2.1.1. Конструктивное выполнение и свойства линии электропередачи 32
2.1.2. Математическая модель линии с распределенными параметрами 34
2.1.3. Математические модели линии в виде схем замещения............ 40
2.1.4. Упрощенные модели ЛЭП................................................................... 48
2.2. Силовой трансформатор................................................................................ 53
2.2.1. Конструктивное выполнение и принцип действия силового трансформатора 53
2.2.2. Электрические и магнитные свойства и параметры силового трансформатора 56
2.2.3. Математические модели силового трансформатора.................. 58
2.2.4. Г-образная и П-образная схемы замещения силового трансформатора 61
2.2.5. Построение внешней характеристики трансформатора........... 64
2.3. Электрическая нагрузка................................................................................. 71
2.3.1. Статические характеристики электрической нагрузки.............. 71
2.3.2. Моделирование электрических нагрузок....................................... 77
3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЭЛЕКТРИЧЕСКИХ СЕТЕЙ....................... 87
3.1. Основы теории графов.................................................................................... 87
3.2. Применение теории графов для моделирования электрических сетей 92
3.3. Матричные формы моделей электрических сетей и их режимов...... 96
3.4. Узловые уравнения установившегося режима......................................... 98
3.5. Формы линейных уравнений установившегося режима и их решение 105
3.6. Нелинейные уравнения установившегося режима.............................. 109
3.7. Моделирование генераторных узлов электрической сети............... 116
3.8. Эквивалентирование схем электрических сетей................................... 123
3.9. Моделирование схем электрических сетей с помощью четырехполюсников 129
3.10. Использование четырехполюсников для эквивалентирования схем электрических сетей 132
4. Построение математических моделей.......................................... 145
4.1. Процесс описания объектов моделирования......................................... 145
4.2. Аналитический метод построения математических моделей.......... 149
4.3. Методы идентификации технических объектов.................................... 151
4.4. Выбор структуры математической модели и вычисление ее параметров 157
5. Модели прогнозирования физических процессов................ 169
5.1. Физические процессы и их характеристики........................................... 169
5.1.1. Классификация физических процессов......................................... 169
5.1.2. Детерминированные процессы........................................................ 171
5.1.3. Случайные процессы......................................................................... 176
5.2. Методологические основы прогнозирования........................................ 180
5.3. Экспоненциальная модель прогнозирования........................................ 183
5.4. Логистическая модель прогнозирования................................................ 185
5.5. Прогнозирование случайных процессов................................................. 196
5.6. Прогнозирование суточных графиков нагрузки................................... 201
5.7. Анализ временных рядов............................................................................. 205
библиографический список........................................................................................ 214
Приложение 1. Глоссарий........................................................................................... 216
Приложение 2. Таблицы соотношений коэффициентов четырехполюсников, параметров элементов ЭЭС и параметров П-образной схемы замещения................................................................................ 222
Лыкин Анатолий Владимирович
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ЭЛЕКТРИЧЕСКИХ СИСТЕМ И ИХ ЭЛЕМЕНТОВ
Е изд., перераб. и доп.
Учебное пособие
Редактор И.Л. Кескевич
Выпускающий редактор И.П. Брованова
Корректор И.Е. Семенова
Дизайн обложки А.В. Ладыжская
Компьютерная верстка С.И. Ткачева
| Подписано в печать 03.03.2009. Формат 60 ´ 84 1/16. Бумага офсетная. Тираж 200 экз. Уч.-изд. л. 13, 25. Печ. л. 14, 25. Изд. № 317. Заказ №. Цена договорная
|
Отпечатано в типографии
Новосибирского государственного технического университета
| Прогнозирование суточных графиков нагрузки
|
Оперативный прогноз суточных графиков нагрузки энергосистемы выполняется на следующие сутки и на несколько суток вперед. На режим потребления электрической энергии огромное влияние оказывают состав потребителей ЭЭС, продолжительность рабочей недели (количество смен в сутки), степень загрузки смен промышленных предприятий, метеорологические факторы, а также некоторые другие.
Существенное значение в составе нагрузки имеет соотношение между промышленными потребителями и коммунально-бытовым сектором (рис. 5.17).
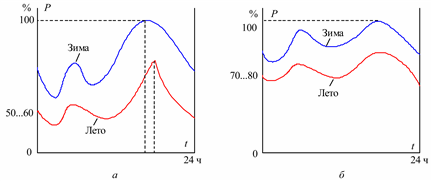 Рис. 5.17. Суточные графики нагрузки: а – со значительной составляющей бытовой нагрузки; б – с преобладанием промышленной нагрузки
Если система имеет значительную бытовую нагрузку, то вечерний максимум значительно больше утреннего (рис. 5.17, а). Эта разница особенно заметна в летнее время. Летом максимум наступает намного позже, чем зимний. Летом максимум – пикообразный, а зимой – пологий. Минимальная нагрузка составляет 50…60 % от максимальной нагрузки.
В энергосистемах с преобладанием промышленной нагрузки имеется два явно выраженных максимума: утренний и вечерний (рис. 5.17, б). Суточный график таких систем более ровный, и минимальная нагрузка составляет 70…80 % от максимальной. В некоторых энергосистемах нагрузка утреннего максимума может быть больше, чем вечернего.
Характер суточного графика нагрузки зависит от освещенности и температуры воздуха (рис. 5.18). При малой освещенности в дневное время нагрузка возрастает и утренний пик становится более продолжительным (рис. 5.18, а). При низкой температуре воздуха нагрузка также возрастает, особенно днем (рис. 5.18, б).
Рис. 5.17. Суточные графики нагрузки: а – со значительной составляющей бытовой нагрузки; б – с преобладанием промышленной нагрузки
Если система имеет значительную бытовую нагрузку, то вечерний максимум значительно больше утреннего (рис. 5.17, а). Эта разница особенно заметна в летнее время. Летом максимум наступает намного позже, чем зимний. Летом максимум – пикообразный, а зимой – пологий. Минимальная нагрузка составляет 50…60 % от максимальной нагрузки.
В энергосистемах с преобладанием промышленной нагрузки имеется два явно выраженных максимума: утренний и вечерний (рис. 5.17, б). Суточный график таких систем более ровный, и минимальная нагрузка составляет 70…80 % от максимальной. В некоторых энергосистемах нагрузка утреннего максимума может быть больше, чем вечернего.
Характер суточного графика нагрузки зависит от освещенности и температуры воздуха (рис. 5.18). При малой освещенности в дневное время нагрузка возрастает и утренний пик становится более продолжительным (рис. 5.18, а). При низкой температуре воздуха нагрузка также возрастает, особенно днем (рис. 5.18, б).
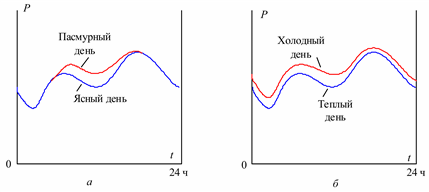 Рис. 5.18. Суточные графики нагрузки: а – при разной освещенности; б – при разной температуре
Наиболее важные графики нагрузки – в период зимнего максимума и летнего минимума, когда следует заботиться о достаточном резерве мощности и соответственно иметь маневренные станции с малым технологическим минимумом. В настоящее время соотношение нагрузок в ЭЭС составляет 0, 5…0, 8.
Суточные графики реактивной мощности ЭЭС в основном определяются потреблением реактивной мощности асинхронными двигателями (примерно 70 % все потребляемой реактивной мощности) и потерями в трансформаторах (около 20 %). На суммарные суточные графики реактивной нагрузки ЭЭС влияют режимы работы линий напряжением 220 кВ и выше, а также общий уровень компенсации реактивной мощности в системе.
На рис. 5.19 показаны суточные графики активной и реактивной нагрузки для двух энергосистем: с преобладанием промышленной нагрузки (рис. 5.19, а) и с преобладанием бытовой нагрузки (рис. 5.19, б).
Системы имеют примерно одинаковые активные нагрузки в утренний и вечерний максимум, но в первой системе утренний максимум реактивной мощности выше вечернего, что объясняется преобладанием в составе нагрузки асинхронных двигателей. Во втором случае вечерняя активная нагрузка выше утренней и вечерний максимум реактивной мощности больше утреннего.
Оперативное прогнозирование суточных графиков нагрузки рабочего дня ЭЭС производится на основании графика предыдущего дня, графика соответствующего дня предыдущей недели и прогноза погоды.
Рис. 5.18. Суточные графики нагрузки: а – при разной освещенности; б – при разной температуре
Наиболее важные графики нагрузки – в период зимнего максимума и летнего минимума, когда следует заботиться о достаточном резерве мощности и соответственно иметь маневренные станции с малым технологическим минимумом. В настоящее время соотношение нагрузок в ЭЭС составляет 0, 5…0, 8.
Суточные графики реактивной мощности ЭЭС в основном определяются потреблением реактивной мощности асинхронными двигателями (примерно 70 % все потребляемой реактивной мощности) и потерями в трансформаторах (около 20 %). На суммарные суточные графики реактивной нагрузки ЭЭС влияют режимы работы линий напряжением 220 кВ и выше, а также общий уровень компенсации реактивной мощности в системе.
На рис. 5.19 показаны суточные графики активной и реактивной нагрузки для двух энергосистем: с преобладанием промышленной нагрузки (рис. 5.19, а) и с преобладанием бытовой нагрузки (рис. 5.19, б).
Системы имеют примерно одинаковые активные нагрузки в утренний и вечерний максимум, но в первой системе утренний максимум реактивной мощности выше вечернего, что объясняется преобладанием в составе нагрузки асинхронных двигателей. Во втором случае вечерняя активная нагрузка выше утренней и вечерний максимум реактивной мощности больше утреннего.
Оперативное прогнозирование суточных графиков нагрузки рабочего дня ЭЭС производится на основании графика предыдущего дня, графика соответствующего дня предыдущей недели и прогноза погоды.
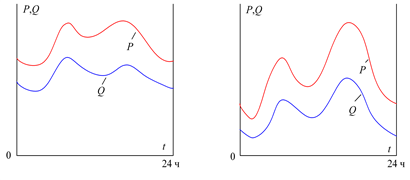 Рис. 5.19. Суточные графики активной и реактивной мощности в ЭЭС: а – с преобладанием промышленной нагрузки; б – с преобладанием бытовой нагрузки
Графики нагрузки выходных дней (суббота, воскресенье), а также послевыходного дня (понедельник) существенно отличаются от графиков обычных выходных дней (рис. 5.20). Они составляются на основании графиков предыдущих выходных и послевыходных дней, прогноза погоды и других влияющих факторов. Погрешность прогноза обычно составляет 2…3 %.
Рис. 5.20. Недельный график мощности нагрузки ЕЭС РФ
Для суточного графика нагрузки различают следующие показатели:
· максимум активной и реактивной нагрузок Pmax и Qmax;
· коэффициент мощности максимума нагрузки cos φ max;
· суточный расход активной и реактивной энергии Wа.сут и Wр.сут;
· средневзвешенный за сутки коэффициент реактивной мощности
Рис. 5.19. Суточные графики активной и реактивной мощности в ЭЭС: а – с преобладанием промышленной нагрузки; б – с преобладанием бытовой нагрузки
Графики нагрузки выходных дней (суббота, воскресенье), а также послевыходного дня (понедельник) существенно отличаются от графиков обычных выходных дней (рис. 5.20). Они составляются на основании графиков предыдущих выходных и послевыходных дней, прогноза погоды и других влияющих факторов. Погрешность прогноза обычно составляет 2…3 %.
Рис. 5.20. Недельный график мощности нагрузки ЕЭС РФ
Для суточного графика нагрузки различают следующие показатели:
· максимум активной и реактивной нагрузок Pmax и Qmax;
· коэффициент мощности максимума нагрузки cos φ max;
· суточный расход активной и реактивной энергии Wа.сут и Wр.сут;
· средневзвешенный за сутки коэффициент реактивной мощности
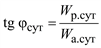 ;
· коэффициенты заполнения суточного графика активной и реактивной энергии ;
· коэффициенты заполнения суточного графика активной и реактивной энергии
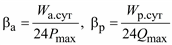 .
Эти показатели полезно иметь как при эксплуатации (оперативный и краткосрочный прогноз), так и при проектировании (долгосрочный прогноз) ЭЭС.
При проектировании ЭЭС суточные графики нагрузок позволяют правильно выбрать суммарную установленную мощность новых электрических станций и их состав.
При прогнозировании суточных графиков нагрузки в проектной постановке используются в основном два подхода: статистический и синтетический.
Статистический подход основан на экстраполяции графиков нагрузки прошлых лет.
Для сопоставимости суточных графиков за разные годы часовые нагрузки представляются в относительных единицах.
Для каждого характерного дня недели каждого месяца строится столько графиков, сколько лет рассматривается.
Вначале прогнозируется форма графика – график в относительных единицах. Затем отдельно рост средней суточной мощности. После этого получается график нагрузки в именованных единицах.
При синтетическом подходе анализируется структура электропотребления каждой группы потребителей и посредством суммирования нагрузок по отдельным группам получается суммарный график ЭЭС .
Эти показатели полезно иметь как при эксплуатации (оперативный и краткосрочный прогноз), так и при проектировании (долгосрочный прогноз) ЭЭС.
При проектировании ЭЭС суточные графики нагрузок позволяют правильно выбрать суммарную установленную мощность новых электрических станций и их состав.
При прогнозировании суточных графиков нагрузки в проектной постановке используются в основном два подхода: статистический и синтетический.
Статистический подход основан на экстраполяции графиков нагрузки прошлых лет.
Для сопоставимости суточных графиков за разные годы часовые нагрузки представляются в относительных единицах.
Для каждого характерного дня недели каждого месяца строится столько графиков, сколько лет рассматривается.
Вначале прогнозируется форма графика – график в относительных единицах. Затем отдельно рост средней суточной мощности. После этого получается график нагрузки в именованных единицах.
При синтетическом подходе анализируется структура электропотребления каждой группы потребителей и посредством суммирования нагрузок по отдельным группам получается суммарный график ЭЭС
|
630092, г. Новосибирск, пр. К. Маркса, 20
Графики нагрузки в ЭЭС являются последовательностями наблюдений или расчетных значений, показывающих изменения мощности в течение определенного периода времени. В суточных, недельных и годовых графиках отображается периодичность процесса изменения мощности нагрузки, связанная с режимом работы людей, сменой дня и ночи, недельными циклами и сезонными изменениями в течение года.
Суточные графики дней недели в общем повторяются изо дня в день с небольшими случайными различиями и режимами выходных и праздничных дней. Средний рост или снижение нагрузки в течение недели или нескольких недель связан с сезонными изменениями, в особенности в осенний и весенний периоды. Такие изменения, происходящие в среднем, относят к трендовым (непериодическим) составляющим графика нагрузки. Эти изменения для годовых графиков обусловлены естественным ростом нагрузки потребителей.
Суточные, недельные и годовые графики нагрузки часто прогнози-руют посредством разделения их на трендовую, периодическую и случайную составляющие:
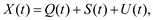 (5.58)
где Q(t) – тренд – устойчивые систематические изменения;
S(t) – периодическая составляющая – колебания относительно тренда;
U(t) – нерегулярная составляющая – случайный шум.
Подобный подход справедлив, если принять гипотезу о том, что резких изменений во временном ряду не произойдет.
Пусть имеется временной ряд значений месячных максимумов мощности нагрузки за несколько лет (рис. 5.21). (5.58)
где Q(t) – тренд – устойчивые систематические изменения;
S(t) – периодическая составляющая – колебания относительно тренда;
U(t) – нерегулярная составляющая – случайный шум.
Подобный подход справедлив, если принять гипотезу о том, что резких изменений во временном ряду не произойдет.
Пусть имеется временной ряд значений месячных максимумов мощности нагрузки за несколько лет (рис. 5.21).
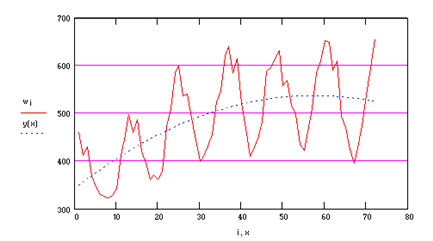 Рис. 5.21. Ретроспектива временного ряда
Для выделения трендовой составляющей часто используют полиномиальную модель до третьего порядка включительно:
Рис. 5.21. Ретроспектива временного ряда
Для выделения трендовой составляющей часто используют полиномиальную модель до третьего порядка включительно:
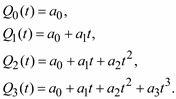 (5.59)
Иногда при выделении тренда предварительно применяют процедуру сглаживания, которая устраняет периодическую и случайную составляющие.
После вычитания из X(t) трендовой составляющей получается временной ряд, имеющий периодическую составляющую, которая вызвана суточными, недельными и сезонными периодами. (5.59)
Иногда при выделении тренда предварительно применяют процедуру сглаживания, которая устраняет периодическую и случайную составляющие.
После вычитания из X(t) трендовой составляющей получается временной ряд, имеющий периодическую составляющую, которая вызвана суточными, недельными и сезонными периодами.
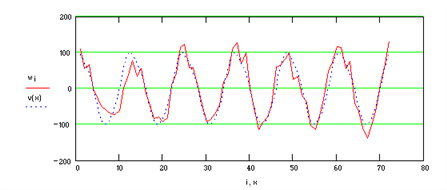 Рис. 5.22. Временной ряд без трендовой составляющей
Если имеется N результатов наблюдений за период T (N = 12 в годовом цикле, N = 7 – в недельном и N = 24 – в суточном), то периодическая модель процесса может быть представлена рядом Фурье
Рис. 5.22. Временной ряд без трендовой составляющей
Если имеется N результатов наблюдений за период T (N = 12 в годовом цикле, N = 7 – в недельном и N = 24 – в суточном), то периодическая модель процесса может быть представлена рядом Фурье
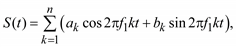 (5.60)
где n – количество частот, включенных в модель.
В общем случае наивысшая частота гармонического разложения дискретного ряда, называемая частотой Найквиста, определяется половиной интервала между наблюдениями, например при N = 12, n = 24. (5.60)
где n – количество частот, включенных в модель.
В общем случае наивысшая частота гармонического разложения дискретного ряда, называемая частотой Найквиста, определяется половиной интервала между наблюдениями, например при N = 12, n = 24.
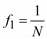 – основная частота гармонического ряда.
Дисперсия, учитываемая i-й гармоникой: – основная частота гармонического ряда.
Дисперсия, учитываемая i-й гармоникой:
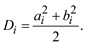 (5.61)
Суммарная дисперсия (5.61)
Суммарная дисперсия 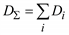 . Как правило, первые три гармоники описывают до 90 % всей дисперсии.
Случайная составляющая . Как правило, первые три гармоники описывают до 90 % всей дисперсии.
Случайная составляющая
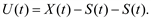 (5.62)
Для U(t) определяются статистические характеристики. Прогноз случайной составляющей ведется по одной из моделей прогноза случайного процесса. Сразу следует оценить интервал корреляции, и если прогноз ведется на время упреждения больше, чем интервал корреляции, то фактически по случайной составляющей оценивается лишь ошибка прогноза, так как после вычитания регулярных составляющих математическое ожидание процесса равно нулю.
Оценка коэффициентов моделей регулярных составляющих
Тренд
Оценка коэффициентов полиномиальной модели тренда может быть сделана разными способами:
1) с помощью функций Mathcad c: = regress(k, P, m) и Qm(t): = in-terp(c, k, P, t). Здесь c – вектор коэффициентов, используемый функцией interp; k – вектор дискретных моментов времени, для которых заданы значения ретроспективы; P – вектор значений ретроспективы; m – порядок полинома (как 0, 1, 2 или 3); t – аргумент функции тренда. Можно также записать Qm(t) = interp(regress(k, P, m), k, P, t);
2) как решение системы линейных уравнений по методу наименьших квадратов A = (VTV)–1VTP. Функция тренда: (5.62)
Для U(t) определяются статистические характеристики. Прогноз случайной составляющей ведется по одной из моделей прогноза случайного процесса. Сразу следует оценить интервал корреляции, и если прогноз ведется на время упреждения больше, чем интервал корреляции, то фактически по случайной составляющей оценивается лишь ошибка прогноза, так как после вычитания регулярных составляющих математическое ожидание процесса равно нулю.
Оценка коэффициентов моделей регулярных составляющих
Тренд
Оценка коэффициентов полиномиальной модели тренда может быть сделана разными способами:
1) с помощью функций Mathcad c: = regress(k, P, m) и Qm(t): = in-terp(c, k, P, t). Здесь c – вектор коэффициентов, используемый функцией interp; k – вектор дискретных моментов времени, для которых заданы значения ретроспективы; P – вектор значений ретроспективы; m – порядок полинома (как 0, 1, 2 или 3); t – аргумент функции тренда. Можно также записать Qm(t) = interp(regress(k, P, m), k, P, t);
2) как решение системы линейных уравнений по методу наименьших квадратов A = (VTV)–1VTP. Функция тренда: 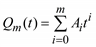 . Здесь V – матрица, первый столбец которой состоит из единиц, второй – вектор k, третий вектор из элементов k в квадрате и т. д. Vi, j = = kij–1 ( i = 1…n, j = 1… m + 1), где n – количество данных ретроспективы.
Экспоненциальная модель тренда может быть получена с помощью функции expfit(k, P, vg), которая возвращает вектор коэффициентов модели . Здесь V – матрица, первый столбец которой состоит из единиц, второй – вектор k, третий вектор из элементов k в квадрате и т. д. Vi, j = = kij–1 ( i = 1…n, j = 1… m + 1), где n – количество данных ретроспективы.
Экспоненциальная модель тренда может быть получена с помощью функции expfit(k, P, vg), которая возвращает вектор коэффициентов модели 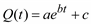 . Здесь вектор vg – начальные приближения для искомых коэффициентов модели.
Периодическая составляющая
Коэффициенты полигармонической составляющей процесса являются коэффициентами гармонического полинома вида (5.60). Вектор коэффициентов модели получается как решение системы линейных уравнений B = (VTV) –1VTW. Здесь V – матрица из n строк и 2m столбцов; n – количество данных ретроспективы; m – количество частот, включенных в модель. Каждая последовательная пара столбцов матрицы V соответствует одной частоте и состоит из коэффициентов, вычисляемых как функции косинуса и синуса из выражения (5.60): . Здесь вектор vg – начальные приближения для искомых коэффициентов модели.
Периодическая составляющая
Коэффициенты полигармонической составляющей процесса являются коэффициентами гармонического полинома вида (5.60). Вектор коэффициентов модели получается как решение системы линейных уравнений B = (VTV) –1VTW. Здесь V – матрица из n строк и 2m столбцов; n – количество данных ретроспективы; m – количество частот, включенных в модель. Каждая последовательная пара столбцов матрицы V соответствует одной частоте и состоит из коэффициентов, вычисляемых как функции косинуса и синуса из выражения (5.60):
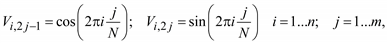 (5.63)
W – вектор, полученный из P вычитанием трендовой составляющей.
Возможно моделирование периодической составляющей с помощью другого представления ряда Фурье: (5.63)
W – вектор, полученный из P вычитанием трендовой составляющей.
Возможно моделирование периодической составляющей с помощью другого представления ряда Фурье:
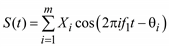 , (5.64)
где искомыми параметрами являются , (5.64)
где искомыми параметрами являются 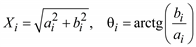 .
Пример. Чтение данных из файла Retro.prn .
Пример. Чтение данных из файла Retro.prn

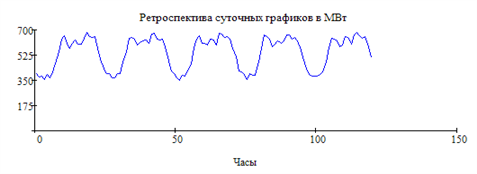
 Представим тренд постоянной функцией, равной среднему значению за 5 суток
Представим тренд постоянной функцией, равной среднему значению за 5 суток
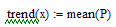
 Остаточный временной ряд без тренда
Остаточный временной ряд без тренда
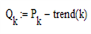
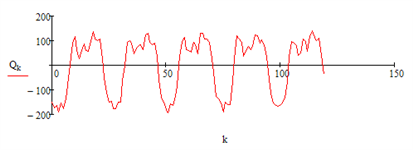 Моделирование периодической составляющей – 6 гармоник:
Моделирование периодической составляющей – 6 гармоник:
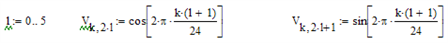
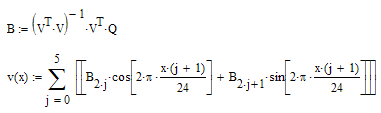 Графическое изображение периодической составляющей:
Графическое изображение периодической составляющей:
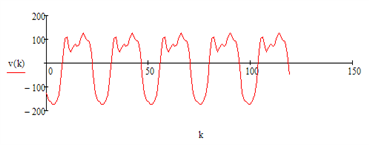 Остаточный временной ряд без тренда и периодической составляющей – случайная составляющая:
Остаточный временной ряд без тренда и периодической составляющей – случайная составляющая:
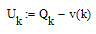
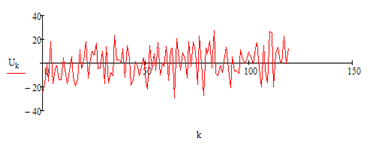 Определение статистических характеристик случайной составляющей временного ряда: среднее значение, медиана, среднеквадратическое отклонение:
Определение статистических характеристик случайной составляющей временного ряда: среднее значение, медиана, среднеквадратическое отклонение:
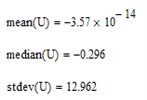 Прогнозируемый график есть сумма тренда и случайной составляющей:
Прогнозируемый график есть сумма тренда и случайной составляющей:
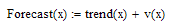
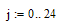
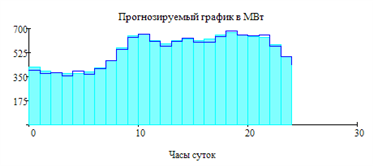 За ошибку прогноза принимаем среднеквадратическое отклонение случайной составляющей временного ряда:
За ошибку прогноза принимаем среднеквадратическое отклонение случайной составляющей временного ряда:
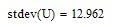
|
* Приведены термины и определения из стандарта организации ОАО РАО «ЕЭС России» ЭЛЕКТРОЭНЕРГЕТИКА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ. Терминологический справочник по электроэнергетике. – М.: Типография «КЕМ», 2008. – 912 с.
Популярное:

