Простейшие интегралы, содержащие квадратный трехчлен
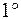 . Интегралы вида
. Интегралы вида 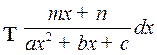 . Основной прием вычисления– приведения квадратного трехчлена к виду:
. Основной прием вычисления– приведения квадратного трехчлена к виду:
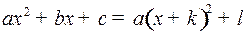 , (1)
, (1)
где  и
и 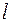 - постоянные. Для выполнения преобразования (1) удобнее всего из квадратного трехчлена выделить полный квадрат. Можно также пользоваться подстановкой
- постоянные. Для выполнения преобразования (1) удобнее всего из квадратного трехчлена выделить полный квадрат. Можно также пользоваться подстановкой
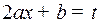 .
.
Если 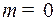 , то приводя квадратный трехчлен к виду (1), получаем табличные интегралы 3 или 4 (см. § 1, 2, таблицу простейших интегралов).
, то приводя квадратный трехчлен к виду (1), получаем табличные интегралы 3 или 4 (см. § 1, 2, таблицу простейших интегралов).
Пример 1. 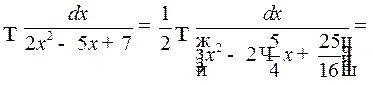
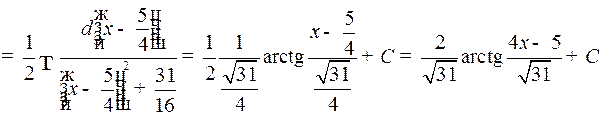 .
.
Если 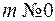 , то из числителя выделяется производная
, то из числителя выделяется производная 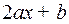 квадратного трехчлена
квадратного трехчлена
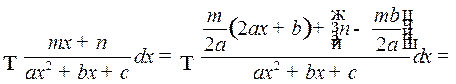
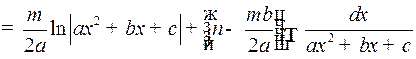 ,
,
и таким образом, мы приходим к интегралу, разобранному выше.
Пример 2. 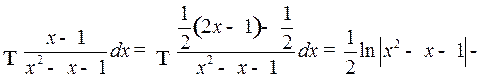
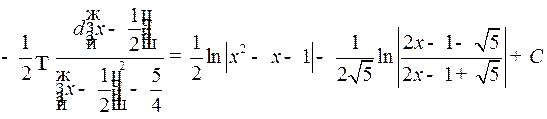 .
.
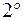 . Интегралы вида
. Интегралы вида 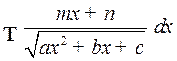 . Методы вычислений аналогичны разобранным выше. В конечном итоге интеграл приводится к табличному интегралу 5, если
. Методы вычислений аналогичны разобранным выше. В конечном итоге интеграл приводится к табличному интегралу 5, если 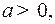 и 6, если
и 6, если 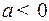 .
.
Пример 3.
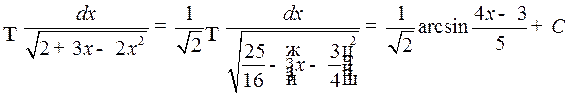 .
.
Пример 4.
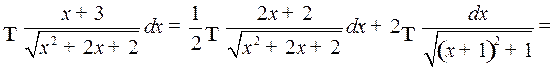
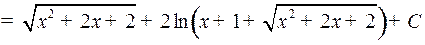 .
.
 . Интегралы вида
. Интегралы вида 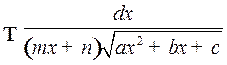 . С помощью обратной подстановки
. С помощью обратной подстановки
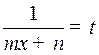
эти интегралы приводятся к интегралам вида 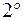 .
.
Пример 5. Найти
 .
.
Решение. Полагаем
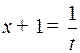 ,
,
отсюда
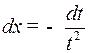 .
.
Имеем: 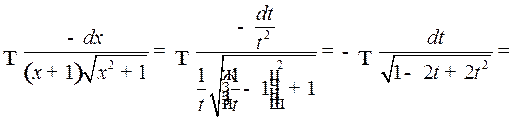
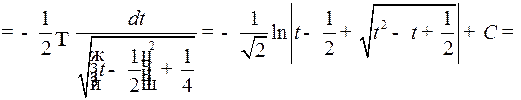
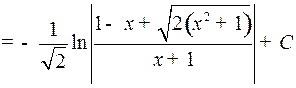 .
.
 . Интегралы вида
. Интегралы вида 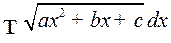 . Путем выделения из квадратного трехчлена полного квадрата данный интеграл сводится к одному из следующих основных интегралов:
. Путем выделения из квадратного трехчлена полного квадрата данный интеграл сводится к одному из следующих основных интегралов:
1) 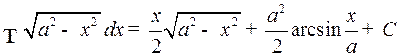 ,
,
2) 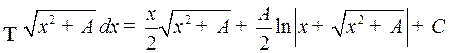 .
.
Пример 6. 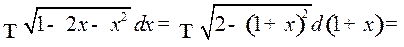
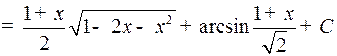 .
.
Интегрирование рациональных функций
 Метод неопределенных коэффициентов. Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби
Метод неопределенных коэффициентов. Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби
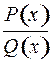 . (1)
. (1)
где 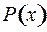 и
и 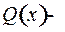 целые многочлены, причем степень числителя
целые многочлены, причем степень числителя 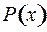 ниже степени знаменателя
ниже степени знаменателя 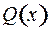 . Если
. Если
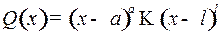 ,
,
где 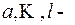 различные действительные корни многочлена
различные действительные корни многочлена 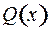 и
и 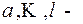 натуральные числа (кратности корней), то справедливо разложение дроби (1) на простейшие дроби:
натуральные числа (кратности корней), то справедливо разложение дроби (1) на простейшие дроби:
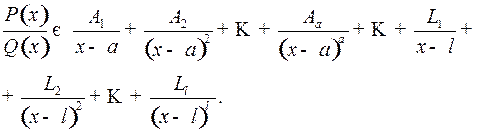 (2)
(2)
Для вычисления неопределенных коэффициентов  обе части тождества (2) приводят к целому виду, а затем приравнивают коэффициенты при одинаковых степенях переменной
обе части тождества (2) приводят к целому виду, а затем приравнивают коэффициенты при одинаковых степенях переменной 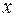 (первый способ). Можно также определять эти коэффициенты, полагая в равенстве (2), или ему эквивалентном,
(первый способ). Можно также определять эти коэффициенты, полагая в равенстве (2), или ему эквивалентном, 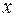 равным подходяще подобранным числам (второй способ).
равным подходяще подобранным числам (второй способ).
Пример 1. Найти
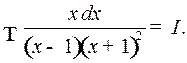
Решение. Имеем:
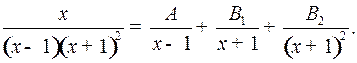
Отсюда
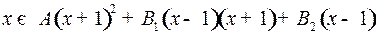 . (3)
. (3)
а) Первый способ определения коэффициентов. Перепишем тождество (3) в виде
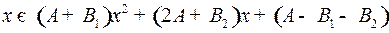 .
.
Приравняв коэффициенты при одинаковых степенях 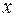 , получим:
, получим:
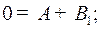
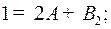
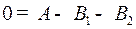 .
.
Отсюда
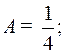
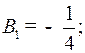
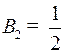 .
.
б) Второй способ определения коэффициентов. Полагая 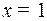
в тождестве (3), будем иметь:
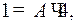 т.е.
т.е. 
Полагая, 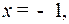 получим:
получим:
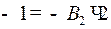 , т.е.
, т.е. 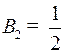 .
.
Далее, полагая 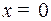 , будем иметь:
, будем иметь:
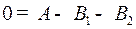 , т.е.
, т.е.  .
.
Следовательно,
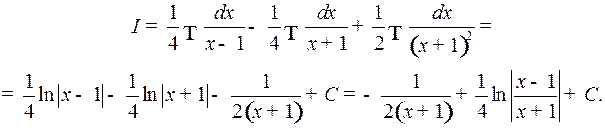
Пример 2. Найти
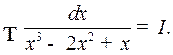
Решение. Имеем:
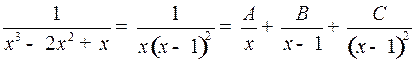
и
 (4)
(4)
При решении этого примера рекомендуется комбинировать два способа определения коэффициентов. Применяя второй способ, полагаем 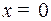 в тождестве (4); получим
в тождестве (4); получим 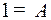 . Затем, полагая
. Затем, полагая 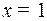 , получим
, получим 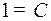 . Далее. Применяя первый способ, приравниваем в тождестве (4) коэффициенты при
. Далее. Применяя первый способ, приравниваем в тождестве (4) коэффициенты при 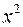 . Будем иметь:
. Будем иметь:
 т.е.
т.е. 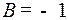 .
.
Таким образом,
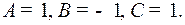
Следовательно,
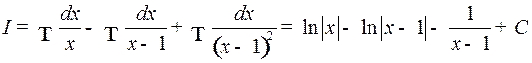 .
.
Если многочлен 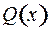 имеет комплексные корни
имеет комплексные корни 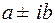 кратности
кратности  , то в разложение (2) дополнительно войдут простейшие дроби вида:
, то в разложение (2) дополнительно войдут простейшие дроби вида:
 , (5)
, (5)
где
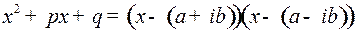
и 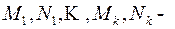 неопределенные коэффициенты, определяемые способами указанными выше. При
неопределенные коэффициенты, определяемые способами указанными выше. При 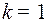 дробь (5) интегрируется непосредственно; при
дробь (5) интегрируется непосредственно; при 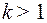 применяется метод понижения, причем предварительно квадратный трехчлен
применяется метод понижения, причем предварительно квадратный трехчлен 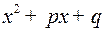 рекомендуется представить в виде
рекомендуется представить в виде 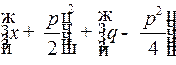 и сделать подстановку
и сделать подстановку 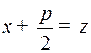 .
.
Пример 3. Найти
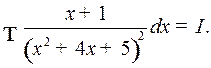
Решение. Так как
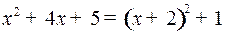 ,
,
то, полагая 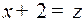 , получим:
, получим:
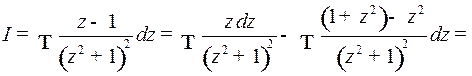
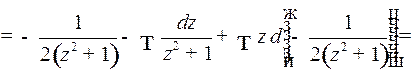
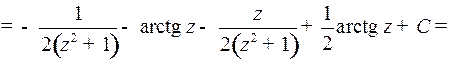
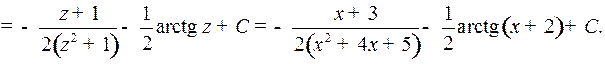
Интегрирование некоторых иррациональных функций
1o. Интегралы вида
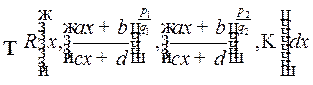 , (1)
, (1)
где 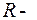 рациональная функция и
рациональная функция и 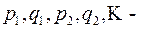 целые числа.
целые числа.
Интегралы вида (1) находятся с помощью подстановки
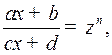
где 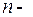 наименьшее общее кратное чисел
наименьшее общее кратное чисел 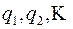 .
.
Пример 1. Найти

Решение. Подстановка 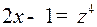 приводит интеграл к виду
приводит интеграл к виду
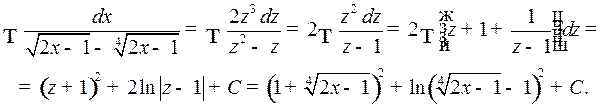
Пример 2. Найти интеграл
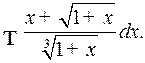
Решение. Наименьшее общее кратное показателей корней в подынтегральном выражении равно 6, поэтому делаем подстановку 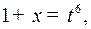 откуда
откуда 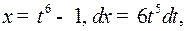 то есть
то есть
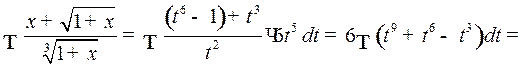
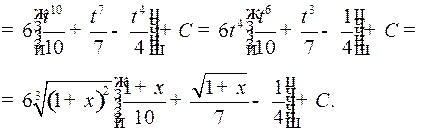
Пример 3. Найти интеграл
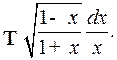
Решение. Сделаем подстановку 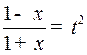 .
.
Отсюда 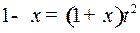 т.е.
т.е. 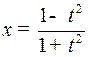 ,
,
и значит,
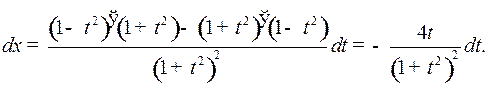
Таким образом,
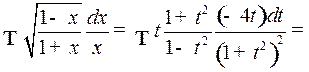
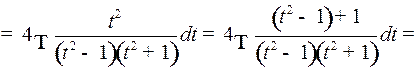
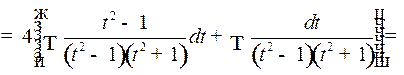
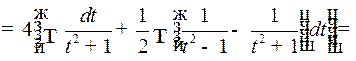
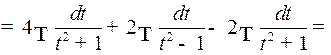
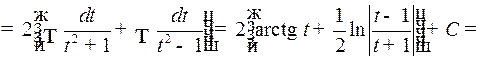
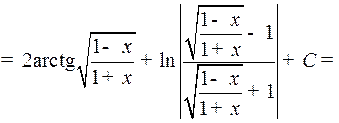
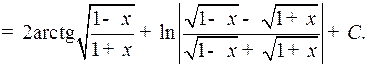
2o. Интегралы вида
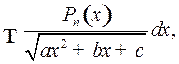
где 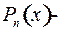 многочлен степени
многочлен степени 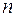 .
.
Полагают,
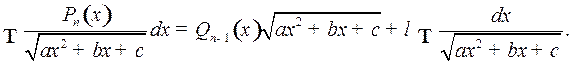 (3)
(3)
где 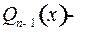 многочлен степени
многочлен степени 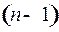 с неопределенными коэффициентами и
с неопределенными коэффициентами и 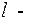 число.
число.
Коэффициенты многочлена 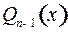 и число
и число 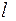 находятся при помощи дифференцирования тождества (3).
находятся при помощи дифференцирования тождества (3).
Пример 4.

Отсюда
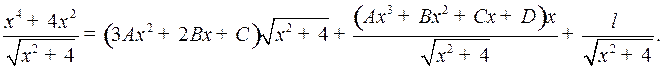
Умножая на 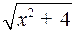 и приравнивая коэффициенты при одинаковых степенях
и приравнивая коэффициенты при одинаковых степенях 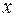 , получим:
, получим:
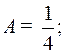

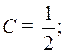
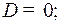
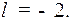
Следовательно,
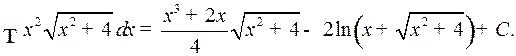
3o . Интегралы вида
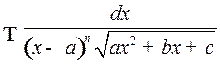 (4)
(4)
приводится к интегралам вида (2) с помощью подстановки
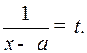
4o . Интегралы от дифференциальных биномов
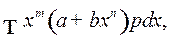 (5)
(5)
где 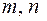 и
и  рациональные числа.
рациональные числа.
Условия Чебышева. Интеграл (5) выражается через конечную комбинацию элементарных функций лишь в следующих трех случаях:
1) если  целое число;
целое число;
2) если 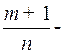 целое число. Здесь применяется подстановка
целое число. Здесь применяется подстановка 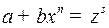 , где
, где 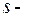 знаменатель дроби
знаменатель дроби 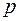 ;
;
3) если 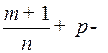 целое число. В этом случае используется подстановка
целое число. В этом случае используется подстановка 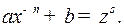
Пример 3. Найти
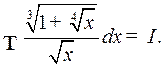
Решение. Здесь 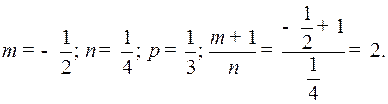
Следовательно, имеет место случай 2) интегрируемости.
Подстановка
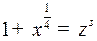
дает: 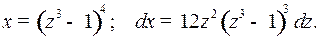
Поэтому
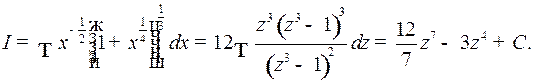
где 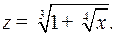
Популярное:
- III Перепишите следующие предложения, содержащие разные формы сравнения и переведите их на русский язык.
- Азотсодержащие органические соединения
- Амфифильные полимеры N-винилпирролидона, содержащие дополнительные функциональные группы
- ГАЗОВЫЕ ЗАКОНЫ. ПРОСТЕЙШИЕ СТЕХИОМЕТРИЧЕСКИЕ
- ДНК-содержащие вирусы Глава 46. Возбудитель натуральной оспы
- Источники права РФ, содержащие коллизионные нормы. Соотношение коллизионных норм ГК РФ и других законов.
- Кислотные металлсодержащие красители
- Классы содержащие другие классы в качестве данных-членов
- Нарушения законодательства о налогах и сборах, содержащие признаки административных правонарушений -(налоговые проступки)
- Органы, содержащие ферменты.
- Переведите предложения, содержащие всевозможные формы причастий: Participle I, Participle II, Perfect Participle Active, Perfect Participle Passive.
- Переведите предложения, содержащие распространенное определение (РО), на русский язык.

