Тема: Динамика поступательного движения.
Тема: Динамика поступательного движения.
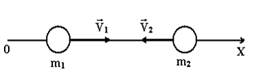 №1
№1
Вдоль оси OX навстречу друг другу движутся две частицы с массами 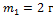 ,
, 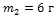 и скоростями
и скоростями 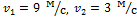 соответственно. Проекция скорости центра масс на ось ОХ (в единицах СИ) равна …
соответственно. Проекция скорости центра масс на ось ОХ (в единицах СИ) равна …
ответ: и 0.0
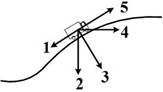 №2
№2
Автомобиль поднимается в гору по участку дуги с увеличивающейся по величине скоростью.
Равнодействующая всех сил, действующих на автомобиль, ориентирована в направлении … Ответ: 4
№3
Импульс материальной точки изменяется по закону 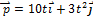 (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 4 c, равен …
(кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 4 c, равен …
Ответ: 26
Решение:
Согласно второму закону Ньютона скорость изменения импульса материальной точки равна действующей на нее силе: 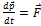 . Тогда зависимость силы от времени имеет вид
. Тогда зависимость силы от времени имеет вид 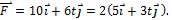 Модуль силы
Модуль силы 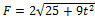 , и в момент времени t = 4 c
, и в момент времени t = 4 c 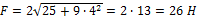
№4
Механическая система состоит из трех частиц, массы которых
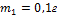 ,
, 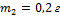 ,
, 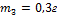 ,. Первая частица находится в точке с координатами (1, 2, 0), вторая – в точке (0, 2, 1), третья – в точке (1, 0, 1) (координаты даны в сантиметрах). Тогда
,. Первая частица находится в точке с координатами (1, 2, 0), вторая – в точке (0, 2, 1), третья – в точке (1, 0, 1) (координаты даны в сантиметрах). Тогда 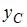 – координата центра масс (в см) – равна … Ответ: 1
– координата центра масс (в см) – равна … Ответ: 1
Решение:
Центром масс системы материальных точек называется точка С, радиус-вектор которой определяется соотношением 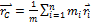 . Тогда
. Тогда 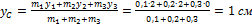
№5
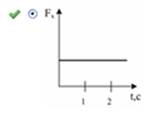
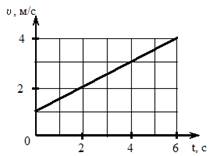 На рисунке приведен график зависимости скорости тела v от времени t.
На рисунке приведен график зависимости скорости тела v от времени t.
Если масса тела равна 2 кг, то сила (в Н), действующая на тело, равна …
Правильный ответ 1
Решение:
Из второго закона Ньютона F=ma, где а – модуль ускорения, который можно найти из графика зависимости v(t): 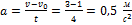 . Тогда
. Тогда 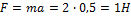
№6 Зависимость импульса частицы от времени описывается законом 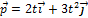 , где
, где 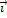 и
и 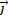 - единичные векторы координатных осей X, Y соответственно. Зависимость горизонтальной проекции силы
- единичные векторы координатных осей X, Y соответственно. Зависимость горизонтальной проекции силы 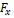 , действующей на частицу, от времени представлена на графике….
, действующей на частицу, от времени представлена на графике….
Решение:
Сила 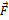 , действующая на материальную точку, равна скорости изменения ее импульса
, действующая на материальную точку, равна скорости изменения ее импульса 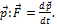 В нашем случае
В нашем случае 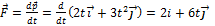 , и, сравнивая
, и, сравнивая 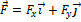 , находим
, находим 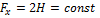 и
и 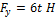 . Проекция силы
. Проекция силы  на ось
на ось 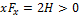 ; следовательно, с течением времени горизонтальная составляющая силы не меняется.
; следовательно, с течением времени горизонтальная составляющая силы не меняется.
№7 На покоящееся тело массы 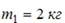 налетает с некоторой скоростью
налетает с некоторой скоростью 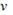 тело массы
тело массы
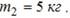 Сила, возникающая при взаимодействии тел, линейно -зависящая от времени, растет от 0 до значения
Сила, возникающая при взаимодействии тел, линейно -зависящая от времени, растет от 0 до значения 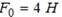 за время
за время 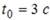 а затем равномерно убывает до нуля за то же время
а затем равномерно убывает до нуля за то же время 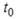 Все движения происходят по одной прямой. Скорость
Все движения происходят по одной прямой. Скорость
первого тела массы 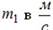 после взаимодействия равна…
после взаимодействия равна…
Решение
Поскольку на тело действует переменная сила, применим второй закон Ньютона в виде 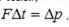 Импульс силы равен изменению механического импульса. Импульс силы взаимодействия равен
Импульс силы равен изменению механического импульса. Импульс силы взаимодействия равен 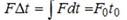
(интеграл можно найти вычислив площадь под графиком функции 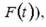 изменение механического импульса
изменение механического импульса 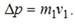 Находим скорость первого тела массы m1 после взаимодействия
Находим скорость первого тела массы m1 после взаимодействия
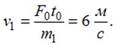
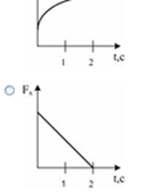
№8 Зависимость импульса частицы от времени описывается законом 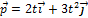 , где
, где 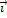 и
и 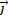 - единичные векторы координатных осей X, Y соответственно. Зависимость горизонтальной проекции силы
- единичные векторы координатных осей X, Y соответственно. Зависимость горизонтальной проекции силы 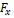 , действующей на частицу, от времени представлена на графике….
, действующей на частицу, от времени представлена на графике….
РЕШЕНИЕ 
Сила 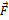 , действующая на материальную точку, равна скорости изменения ее импульса
, действующая на материальную точку, равна скорости изменения ее импульса 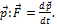 В нашем случае
В нашем случае 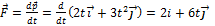 , и, сравнивая
, и, сравнивая 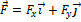 , находим
, находим 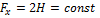 и
и 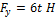 . Проекция силы
. Проекция силы 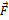 на ось
на ось 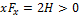 ; следовательно, с течением времени горизонтальная составляющая силы не меняется.
; следовательно, с течением времени горизонтальная составляющая силы не меняется.
№9
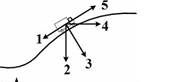 Модуль скорости автомобиля изменялся со временем, как показано на графике зависимости 𝞾 (t).В момент времени
Модуль скорости автомобиля изменялся со временем, как показано на графике зависимости 𝞾 (t).В момент времени 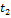 автомобиль поднимался по участку дуги.
автомобиль поднимался по участку дуги.
Направление результирующей всех сил, действующих на автомобиль в этот момент времени, правильно отображает вектор…
Решение:
 В системе отсчета, связанной с Землей, ускорение автомобиля
В системе отсчета, связанной с Землей, ускорение автомобиля  и результирующая действующих на него сил
и результирующая действующих на него сил  связаны вторым законом Ньютона:
связаны вторым законом Ньютона: 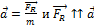 . Полное ускорение
. Полное ускорение 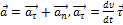 - тангенциальная состовляющая ускорения,
- тангенциальная состовляющая ускорения, 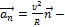 нормальная состовляющая ускорения.Как следует из графика зависимости модуля скорости от времени, в момент
нормальная состовляющая ускорения.Как следует из графика зависимости модуля скорости от времени, в момент 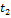 модуль скорости автомобиля достигает максимального значения
модуль скорости автомобиля достигает максимального значения 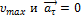 . Поскольку автомобиль движется в этот момент по криволинейному участку траектории, то
. Поскольку автомобиль движется в этот момент по криволинейному участку траектории, то 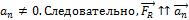 (см.рисунок) и ее направление совпадает с напрвление вектора 3.Ответ: вектор 3
(см.рисунок) и ее направление совпадает с напрвление вектора 3.Ответ: вектор 3
Решение.
При одинаковом моменте сил угловое ускорение обратно пропорционально моменту инерции тела. Момент инерции шара 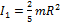 , момент инерции цилиндра
, момент инерции цилиндра 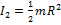 , момент инерции тонкостенного цилиндра
, момент инерции тонкостенного цилиндра 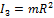 . Следовательно, ускорение торможения будет большим для шара и первым остановится шар.
. Следовательно, ускорение торможения будет большим для шара и первым остановится шар.
Цилиндр
ü Шар
Тонкостенный цилиндр цилиндр с шаром
цилиндр с шаром
№9
Величина момента импульса тела относительно неподвижной оси изменяется по закону L(t)=-1/3 t^3+4t при этом зависимость величины момента сил, действующих на тело, описывается графиком…
Решение:
Скорость изменения момента импульса относительно какой-то неподвижной оси равна величине суммарного момента внешних сил относительно этой оси, т.е. 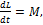 где L-величина момента импульса, M –величина момента сил. Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим зависимость величины момента сил от времени
где L-величина момента импульса, M –величина момента сил. Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим зависимость величины момента сил от времени 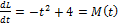 .
.
Графиком этой функции является убывающая ветвь параболы.
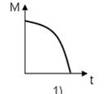
Ответ: 1)
РЕШЕНИЕ
Найдем скорость: 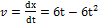 . При t =1c,
. При t =1c, 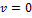 . Средняя скорость за время движения до остановки
. Средняя скорость за время движения до остановки 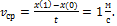 Ответ: 1
Ответ: 1 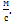
№8
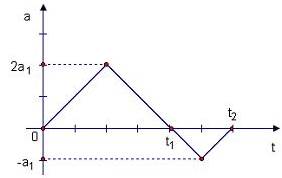
На графике показано изменение с течением времени ускорения точки на прямолинейном отрезке пути. Начальная скорость равна нулю. Скорость точки в момент времени 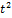 равна …
равна …
Решение.
Площадь, ограниченная графиком, представляет собой приращение скорости. За время движения 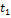 приращение скорости положительно и равно
приращение скорости положительно и равно 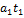 . За время
. За время 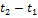 приращение скорости отрицательно и равно
приращение скорости отрицательно и равно 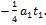 Поскольку начальная скорость равна нулю, то скорость в момент времени
Поскольку начальная скорость равна нулю, то скорость в момент времени 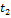 равна
равна
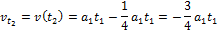
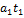
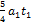
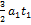
ü 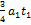
 №9
№9
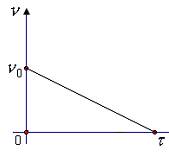
Ротор электродвигателя, вращающийся со скоростью  , после выключения остановился через
, после выключения остановился через  Угловое ускорение торможения ротора после выключения электродвигателя оставалось постоянным. Зависимость частоты вращения от времени торможения показана на графике. Число оборотов, которые сделал ротор до остановки, равно …
Угловое ускорение торможения ротора после выключения электродвигателя оставалось постоянным. Зависимость частоты вращения от времени торможения показана на графике. Число оборотов, которые сделал ротор до остановки, равно …
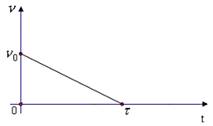 Решение.
Решение.
Начальная частота 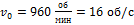 , конечна частота
, конечна частота 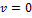 . Площадь, ограниченная графиком и осью абсцисс, равна числу оборотов, сделанных до остановки. Время
. Площадь, ограниченная графиком и осью абсцисс, равна числу оборотов, сделанных до остановки. Время 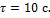 Вычисляя площадь треугольника, получим
Вычисляя площадь треугольника, получим 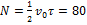 .
.
№10
Цилиндр радиуса R катится без скольжения по горизонтальной плоскости со скоростью 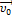 .
.
Точка М расположена на нижней половине вертикального диаметра цилиндра на расстоянии r от центра цилиндра.Зависимость мгновенной скорости точки M от расстояния до центра цилиндра имеет вид…
Решение:
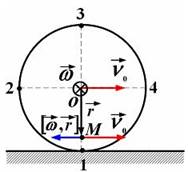 Движение точек цилиндра можно представить как результат сложения двух движений: поступательного со скоростью
Движение точек цилиндра можно представить как результат сложения двух движений: поступательного со скоростью  и вращательного относительно оси цилиндра с угловой скоростью
и вращательного относительно оси цилиндра с угловой скоростью 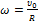 .Линейная скорость вращения относительно оси цилиндра равна
.Линейная скорость вращения относительно оси цилиндра равна 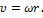
Для точек на нижней половине вертикального диаметра цилиндра эти скорости направлены противоположно. Поэтому скорость точки М равна 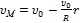 и график зависимости мгновенной скорости точки М от расстояния r до оси цилиндра имеет вид:
и график зависимости мгновенной скорости точки М от расстояния r до оси цилиндра имеет вид: 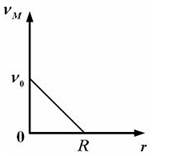
Качение цилиндра можно также представить как вращение относительно мгновенной оси вращения, которой является образующая цилиндра, касающаяся в данный момент горизонтальной плоскости.
№11
Твердое тело начинает вращаться вокруг оси z.Зависимость углового ускорения 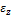 от времени t представлена на графике
от времени t представлена на графике
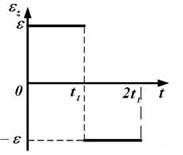
Соответствующая зависимость угловой скорости  от времени представлена графиком…
от времени представлена графиком…
Решение:
Угловое ускорение характеризует быстроту изменения угловой скорости тела 
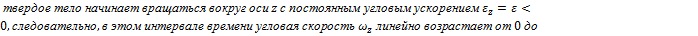
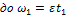 (см.рис.).В интервале времени от
(см.рис.).В интервале времени от 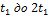 проекция углового ускорения меняет знак,
проекция углового ускорения меняет знак,
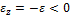 , значит, угловая скорость в этом интервале будет линейно убывать от значения
, значит, угловая скорость в этом интервале будет линейно убывать от значения 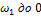 (см.рис.).
(см.рис.).
№12
Тело брошено с поверхности Земли со скоростью 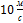 под углом 45
под углом 45 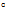 к горизонту.Если сопротивлением воздуха принебречь и принять
к горизонту.Если сопротивлением воздуха принебречь и принять 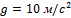 , то радиус кривизны траектории в верхней точке в м равен …
, то радиус кривизны траектории в верхней точке в м равен …
Решение:
Начальная скорость 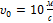 направлена под углом 45
направлена под углом 45 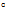 к горизонту.Проекция скорости на горизонтальное направление остается неизменой,
к горизонту.Проекция скорости на горизонтальное направление остается неизменой, 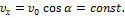 В верхней точке траектории скорость направлена горизонтально и ускорение свободного падения становится нормальным ускорением.По формуле для нормального ускорения
В верхней точке траектории скорость направлена горизонтально и ускорение свободного падения становится нормальным ускорением.По формуле для нормального ускорения 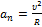 находим радиус кривизны траектории:
находим радиус кривизны траектории: 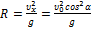 .Подставляя числовые значения, получим R=5 м.
.Подставляя числовые значения, получим R=5 м.
Тема: Работа. Энергия
№1 Частица совершила перемещение по некоторой траектории из точки 1 с радиус-вектором 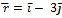 в точку 2 с радиус-вектором
в точку 2 с радиус-вектором 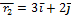 . При этом на нее действовала сила
. При этом на нее действовала сила 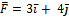 (радиус-векторы
(радиус-векторы 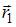 ,
, 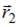 и сила
и сила 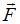 заданы в единицах СИ). Работа, совершенная силой
заданы в единицах СИ). Работа, совершенная силой 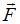 , равна … ответ: 26
, равна … ответ: 26
Решение:
По определению 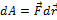 . С учетом того, что
. С учетом того, что 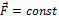 ,
,
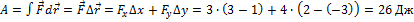
№2 На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Момент импульса первого тела
L1 = 0, 1 Дж·с. Если m = 1 кг, R = 10см, то кинетическая энергия второго тела (в мДж) равна …
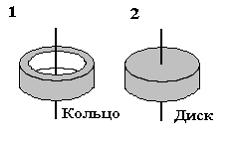 ответ: 250
ответ: 250
№3
Тело массы m=100г бросили с поверхности земли с начальной скоростью v0 = 10 м/с под углом α = 30° к горизонту. Если пренебречь сопротивлением воздуха, средняя мощность, развиваемая силой тяжести за время падения тела на землю, равна …
Ответ: 0
Решение:
Средняя мощность, развиваемая силой за некоторый промежуток времени, равна отношению работы, совершаемой силой за рассматриваемый промежуток времени, к длительности этого промежутка: 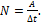 Работа силы тяжести
Работа силы тяжести 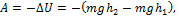 и
и 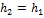 по условию задачи. Тогда A = 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, также равна нулю.
по условию задачи. Тогда A = 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, также равна нулю.
№4
Потенциальная энергия частицы задается функцией 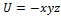 .
. 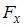 -компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна …
-компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна …
(Функция 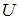 и координаты точки А заданы в единицах СИ.) Ответ: 6
и координаты точки А заданы в единицах СИ.) Ответ: 6
Решение:
Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид 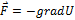 , или
, или 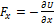 ,
, 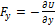 ,
, 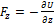 . Таким образом,
. Таким образом, 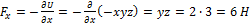 .
.
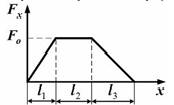 №5 Тело движется вдоль оси
№5 Тело движется вдоль оси 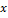 под действием силы, зависимость которой от координаты
под действием силы, зависимость которой от координаты 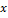 представлена на рисунке:
представлена на рисунке:
Работа силы на пути 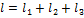 определяется выражением …
определяется выражением …
Решение:
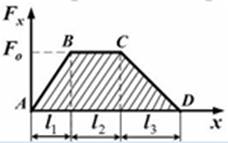 Работа переменной силы в случае одномерного движения на участке
Работа переменной силы в случае одномерного движения на участке 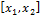 определяется как интеграл:
определяется как интеграл: 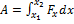 . На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту:
. На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту:
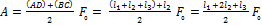 .
.
РЕШЕНИЕ
Закон равных площадей или 2-й закон Кеплера является следствием закона сохранения момента импульса для движения в центральном поле.
Выразим момент импульса тела через заданные параметры начального положения: 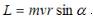 . Из закона сохранения момента импульса следует, что величина
. Из закона сохранения момента импульса следует, что величина 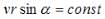 , т.е. должна оставаться постоянной в процессе движения. Площадь, описываемая радиус-вектором за бесконечно малый промежуток времени будет равна площади треугольника с гипотенузой r, катетами
, т.е. должна оставаться постоянной в процессе движения. Площадь, описываемая радиус-вектором за бесконечно малый промежуток времени будет равна площади треугольника с гипотенузой r, катетами 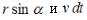 , т.е.
, т.е. 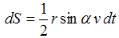 . Следовательно, за время t радиус-вектор, проведенный от Солнца к планете, опишет площадь
. Следовательно, за время t радиус-вектор, проведенный от Солнца к планете, опишет площадь 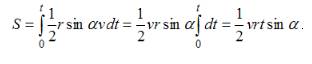
№8
Шар и полная сфера, имеющие одинаковые массы и радиусы, вкладываются без проскальзывания на горку. Если начальные скорости этих тел одинаковы, то …
Решение: 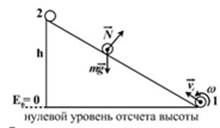
Воспользуемся законом сохраненья механической энергии. Полная энергия тел не изменяется, поэтому
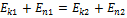 . Здесь 1 и 2 –состояния системы,
. Здесь 1 и 2 –состояния системы, 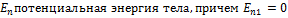 , и кинематическая энергия плоского движения твердого тела равна сумме кинематической энергии поступательного движения и кинематической энергии вращения вокруг оси, проходящей через центр масс:
, и кинематическая энергия плоского движения твердого тела равна сумме кинематической энергии поступательного движения и кинематической энергии вращения вокруг оси, проходящей через центр масс: 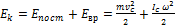 . В последней формуле
. В последней формуле 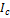 - момент инерции тела относительно оси, В последней формуле
- момент инерции тела относительно оси, В последней формуле 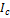 – момент инерции тела относительно оси, проходящий через его центр масс;
– момент инерции тела относительно оси, проходящий через его центр масс; 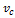 –скорость его центра масс. Из условия отсутствия проскальзывания следует, что мгновенные скорости точек касания тела о горку равны нулю, то есть угловая скорость
–скорость его центра масс. Из условия отсутствия проскальзывания следует, что мгновенные скорости точек касания тела о горку равны нулю, то есть угловая скорость 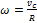 .В нашем случае, энергии тела в первом и во втором состояниях равны:
.В нашем случае, энергии тела в первом и во втором состояниях равны: 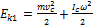 ,
, 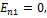
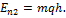 Из закона сохранения энергии
Из закона сохранения энергии 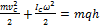 следует
следует 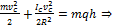
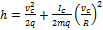 .
.
Анализируя последнюю формулу, видим, что при равенстве масс, скоростей радиусов однородного шара и полой сферы 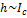 . Сравним моменты инерции тел, обозначив их у шара
. Сравним моменты инерции тел, обозначив их у шара 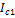 , у полой сферы -
, у полой сферы - 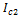 . Момент инерции
. Момент инерции 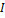 –величина, характеризующая распределение массы тела относительно оси вращения и являющаяся мерой инертности тела при вращательном движении. Вся масса полой сферы находится на расстоянии
–величина, характеризующая распределение массы тела относительно оси вращения и являющаяся мерой инертности тела при вращательном движении. Вся масса полой сферы находится на расстоянии 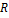 от оси вращения, а у шара распределена равномерно вдоль радиуса сферы. Тогда
от оси вращения, а у шара распределена равномерно вдоль радиуса сферы. Тогда 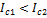 , следовательно,
, следовательно,  . Значит, полая сфера поднимается на горку выше, чем однородный шар.
. Значит, полая сфера поднимается на горку выше, чем однородный шар.
Оба тела поднимутся на одну и ту же высоту
Высоту подъема тел невозможно определить
ü Выше поднимается полая сфера
Выше поднимается шар
№9
Находясь на расстоянии r 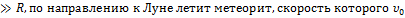 .
.

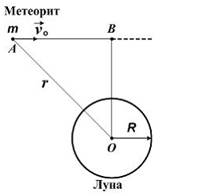
Для расчета минимального прицельного расстояния OB, при котором метеорит не упадет на поверхность Луны, используют законы сохранения механической энергии и момента импульса.Выберите из предложенных вариантов верную запись этих законов. Радиус R и массу M планеты Луна, гравитационную постоянную G, скорость метеорита вблизи поверхности Луны 𝞾 считать известными.
Решение:
Метеорит массой m должен двигаться по гиперболической орбите, касающейся поверхности Луны в точке C.
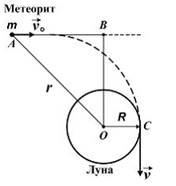
При движении по этой траектории выполняется закон сохранения механической энергии:
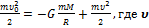 - скорость метеорита вблизи Луны.Действительно, метеорит приближается к Луне под действием силы тяготения.работа этой силы является мерой увеличения кинетической энергии метеорита (скорость метеорита увеличивается 𝞾
- скорость метеорита вблизи Луны.Действительно, метеорит приближается к Луне под действием силы тяготения.работа этой силы является мерой увеличения кинетической энергии метеорита (скорость метеорита увеличивается 𝞾 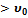 ) и одновременно мерой уменьшения его потенциальной энергии от 0 в точке А до
) и одновременно мерой уменьшения его потенциальной энергии от 0 в точке А до 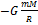 в точке С.Луна из-за большой массы в процессе взаимодействия будет оставаться
в точке С.Луна из-за большой массы в процессе взаимодействия будет оставаться
В покое, а вследствие равенства нулю момента силы притяжения относительно центра Луны момент импульса метеорита относительно центра Луны будет сохраняться: 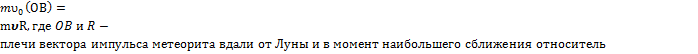
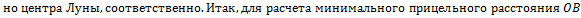
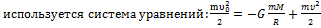 , m
, m 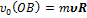 .
.
Решение
Из отношения 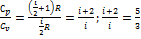 найдем
найдем 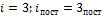 , . Только 3 поступательные степени свободы имеют одноатомные газы, следовательно, это гелий.
, . Только 3 поступательные степени свободы имеют одноатомные газы, следовательно, это гелий.
№5 Средняя кинематическая энергия молекул газа при температуре 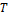 зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекул азота
зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекул азота 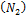 равна …
равна …
Решение:
Для статической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 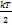 , а на каждую колебательную степень –
, а на каждую колебательную степень – 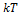 . Средняя кинетическая энергия молекулы равна
. Средняя кинетическая энергия молекулы равна 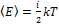 ; где
; где 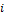 –сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней свободы равна
–сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней свободы равна 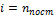 +
+ 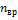 -число степеней свободы поступательного движения, равное
-число степеней свободы поступательного движения, равное 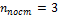 ;
; 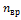 –число степеней свободы вращательного движения, которое может быть равно
–число степеней свободы вращательного движения, которое может быть равно 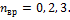 Для молекулярного азота (двухатомной молекулы)
Для молекулярного азота (двухатомной молекулы) 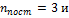
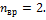
 Следовательно,
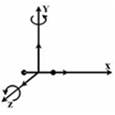
Следовательно, 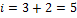 (3 степени свободы поступательного движения по направлениям осей ординат
(3 степени свободы поступательного движения по направлениям осей ординат 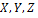 и 2 степени свободы вращательного движения вокруг осей
и 2 степени свободы вращательного движения вокруг осей 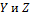 ) (см. рис.) Тогда средняя энергия молекул азота
) (см. рис.) Тогда средняя энергия молекул азота 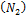 равна
равна 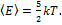
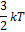
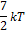
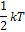
ü 
№6
На каждую степень свободы движения молекулы проходится одинаковая энергия, равная 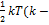 постоянная Больцмана,
постоянная Больцмана, 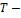 температура по шкале Кельвина). Средняя кинематическая энергия атомного водорода равна …
температура по шкале Кельвина). Средняя кинематическая энергия атомного водорода равна …
Решение.
Средняя кинематическая энергия молекул равна 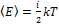 , где
, где 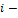 число степеней свободы молекулы. Атомарный водород –это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении
число степеней свободы молекулы. Атомарный водород –это одноатомный газ, атомы которого в данной модели участвуют только в поступательном движении 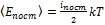 . Число степеней свободы
. Число степеней свободы 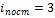 , т.к. положение центра инерции атома задается тремя координатами
, т.к. положение центра инерции атома задается тремя координатами 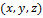 . Следовательно,
. Следовательно, 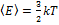 .
.
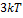
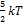
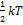
ü 
№7
Средняя кинетическая энергия молекул газа при температуре Т зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы.При условии, что имеет место только поступательное и вращательное движение молекулы, как целого средняя кинетическая энергия молекул азота 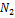 равна..
равна..
Решение:
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия равная 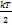 , а на каждую колебательную степень- kT.Средняя кинетическая энергия молекулы равна
, а на каждую колебательную степень- kT.Средняя кинетическая энергия молекулы равна 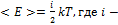 сумма числа поступательных, вращательных и удвоенного числа степеней свободы молекул. При условии, что имеет место только поступательное и вращательное движение, сумма числа степеней свободы равна
сумма числа поступательных, вращательных и удвоенного числа степеней свободы молекул. При условии, что имеет место только поступательное и вращательное движение, сумма числа степеней свободы равна 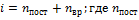 -число степеней свободы поступательного движения, равное
-число степеней свободы поступательного движения, равное 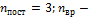 число степеней свободы вращательного движения, которое может быть равно
число степеней свободы вращательного движения, которое может быть равно 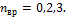 Для молекулярного азота(двухатомной молекулы)
Для молекулярного азота(двухатомной молекулы) 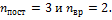 Следовательно,
Следовательно, 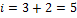 (3 степени поступательно движения по направлениям осей ординатX, Y, Z и 2 степени вращательного движения вокруг осей Y и Z(см.рис.)Тогда средняя кинетическая энергия молекул азота равна
(3 степени поступательно движения по направлениям осей ординатX, Y, Z и 2 степени вращательного движения вокруг осей Y и Z(см.рис.)Тогда средняя кинетическая энергия молекул азота равна
ОТВЕТ: 
Правильный ответ 2.
№5
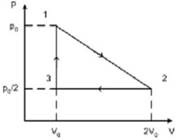 На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке …
На рисунке изображен цилиндрический процесс, происходящий с одним молем двухатомного идеального газа. Газ совершает работу только за счет полученного извне тепла на участке …
Решение.
Из графика видно, что газ получает теплоту в процессах 1-2 и 3-1.
Переход 3-1 осуществляется при постоянном объеме, следовательно, работа газа 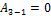 . Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к.
. Из графика видно, что точки 1 и 2 лежат на одной изотерме, т.к.
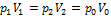 ; следовательно,
; следовательно, 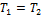 и изменение внутренней энергии
и изменение внутренней энергии 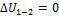 . По
. По 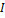 началу термодинамики для процесса 1-2 количество теплоты равно:
началу термодинамики для процесса 1-2 количество теплоты равно:
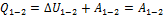 , т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.
, т.е. газ совершает работу за счет полученного извне тепла. Процесс 2-3 является изобарным сжатием, газ передает тепло внешней среде.
3-1
ü 1-2
1-2, 2-3
2-3
№6
Идеальный газ переводится из первого состояния во второе двумя способами(1а2 и 1b2), как показано на рисунке.Теплота, полученная газом, изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связаны соотношениями…
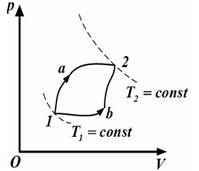
При любом способе перехода идеального газа из первого состояния во второе, согласно первому началу термодинамики, теплота, сообщаемая газу, расходуется на изменение его внутренней энергии и на совершение им работы против внешних сил: 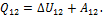 При этом изменение внутренней энергии, как однозначной функции термодинамического состояния системы,
При этом изменение внутренней энергии, как однозначной функции термодинамического состояния системы, 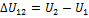 не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний:
не зависит от способа перехода и определяется только разностью значений внутренней энергии этих состояний: 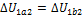 .Работа
.Работа 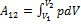 , совершаемая газом при изменение его объема от
, совершаемая газом при изменение его объема от 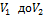 , зависит от процесса перехода.Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p, V(см.рис.).
, зависит от процесса перехода.Величина этой работы равна площади фигуры под графиком процесса в кординатных осях p, V(см.рис.).
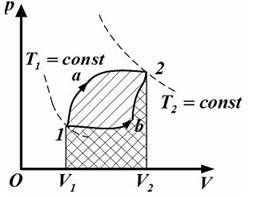
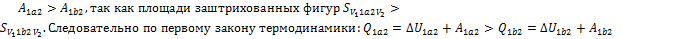 .Теплота, полученая газом, изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями:
.Теплота, полученая газом, изменение внутренней энергии и работа газа при переходе его из одного состояния в другое связы соотношениями: 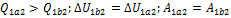 .
.
Правильный ответ 5
Решение:
Работа внешних сил по перемещению заряда в электростатическом поле определяется по формуле 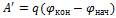 , где q – перемещаемый заряд,
, где q – перемещаемый заряд, 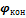 и
и 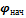 – потенциалы конечной и начальной точек соответственно. Тогда искомая работа
– потенциалы конечной и начальной точек соответственно. Тогда искомая работа 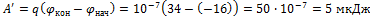
№2
Электростатическое поле создано системой точечных зарядов -q, +q и -q.
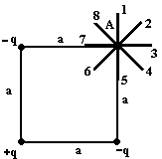
Градиент потенциала поля в точке А ориентирован в направлении … 2
Решение:
Градиент потенциала в некоторой точке связан с напряженностью поля в этой точке соотношением 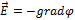 , поэтому для нахождения
, поэтому для нахождения  в вершине квадрата необходимо найти напряженность поля в этой точке. Согласно принципу суперпозиции полей напряженность в точке А равна:
в вершине квадрата необходимо найти напряженность поля в этой точке. Согласно принципу суперпозиции полей напряженность в точке А равна: 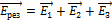 , где
, где 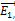
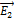 и
и 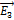 – напряженности полей, создаваемых точечными зарядами –q, +q и –q в рассматриваемой точке соответственно. На рисунке показаны направления этих
– напряженности полей, создаваемых точечными зарядами –q, +q и –q в рассматриваемой точке соответственно. На рисунке показаны направления этих 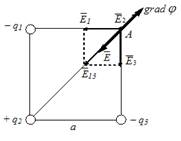 векторов.
векторов.
Величина напряженности поля точечного заряда определяется по формуле 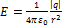 , где
, где 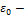 электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине, а заряд +q удален от рассматриваемой точки на расстояние
электрическая постоянная, а r – расстояние от заряда до точки. Поскольку все заряды одинаковы по величине, а заряд +q удален от рассматриваемой точки на расстояние 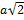 , то
, то 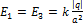 , а
, а 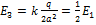 . Модуль вектора
. Модуль вектора 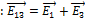 равен диагонали квадрата, построенного на векторах
равен диагонали квадрата, построенного на векторах  и
и  ,, то есть
,, то есть 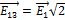 . Таким образом, модуль напряженности результирующего поля в точке А, а сам вектор:
. Таким образом, модуль напряженности результирующего поля в точке А, а сам вектор: 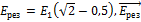 ориентирован в направлении 6. Тогда вектор
ориентирован в направлении 6. Тогда вектор  ориентирован в направлении 2.
ориентирован в направлении 2.
№3 Электростатическое поле создано системой точечных зарядов.
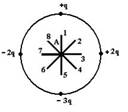 Вектор напряженности
Вектор напряженности 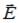 поля в точке А ориентирован в направлении … 6
поля в точке А ориентирован в направлении … 6
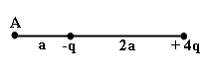 №4 Электростатическое поле создано двумя точечными зарядами: -q и +4q.
№4 Электростатическое поле создано двумя точечными зарядами: -q и +4q.
Отношение потенциала поля, созданного вторым зарядом в точке А, к потенциалу результирующего поля в этой точке равно …
4
№5 На рисунках представлены графики зависимости напряженности поля E( r) для различных распределений заряда:
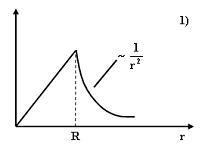
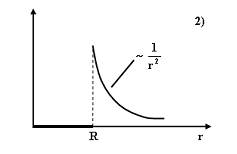
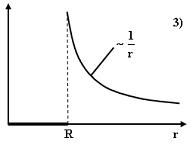
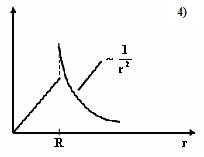
График зависимости E( r) для заряженной металлической сферы радиуса R показан на рисунке 2
№6 Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом 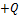 , по перемещению отрицательного заряда
, по перемещению отрицательного заряда  и траекторией перемещения ( указаны начальная и конечная точка).
и траекторией перемещения ( указаны начальная и конечная точка).
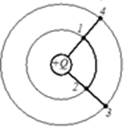
1. 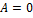
2. 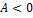
Решение:

