Тема: Кинематика поступательного и вращательного движения
№1
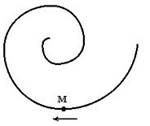 Точка М движется по спирали с равномерно возрастающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …
Точка М движется по спирали с равномерно возрастающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …
 Увеличивается
Увеличивается
Уменьшается
Не изменяется
Равна нулю
№2
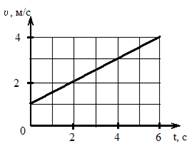 Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, изменяется со временем в соответствии с графиком, представленным на рисунке.
Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, изменяется со временем в соответствии с графиком, представленным на рисунке.
Зависимость угловой скорости тела от времени (в единицах СИ) задается уравнением …

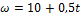
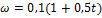
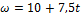
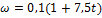
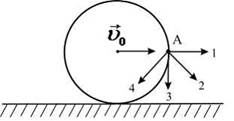
№3 Диск катится равномерно по горизонтальной поверхности со скоростью 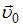 без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …
без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …

 2
2
Решение:
Качение однородного кругового цилиндра (диска) по плоскости является плоским движением. Плоское движение можно представить как совокупность двух движений: поступательного, происходящего со скоростью 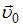 центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда
центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда
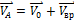 . Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что
. Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что 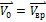 . Вектор
. Вектор 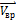 . направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 3). Тогда вектор скорости
. направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 3). Тогда вектор скорости  . точки А ориентирован в направлении 2.
. точки А ориентирован в направлении 2.
№4
Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике.
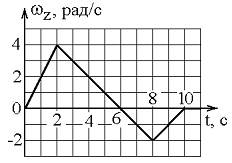
Угловое перемещение (в радианах) в промежутке времени от 2 с до 4 с равно
 6
6
№5 Прямолинейное движение точки описывается уравнением 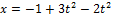 ( в единицах СИ). Средняя скорость точки за время движения до остановки в
( в единицах СИ). Средняя скорость точки за время движения до остановки в 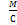 равна…
равна…
Решение:
Найдем скорость: 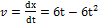 . При t =1c,
. При t =1c, 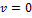 . Средняя скорость за время движения до остановки
. Средняя скорость за время движения до остановки 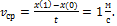 Ответ: 1
Ответ: 1 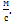
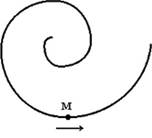
№6 Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения...
 РЕШЕНИЕ
РЕШЕНИЕ
Где R - радиус кривизны траектории в данной точке;
 единичный вектор, перпендикулярный к касательной траектории в данной точке; v - модуль вектора скорости точки. При движении по спирали в направлении, указанном стрелкой. Радиус кривизны R увеличивается. Следовательно, при постоянной скорости v величина нормального ускорения увеличивается.
единичный вектор, перпендикулярный к касательной траектории в данной точке; v - модуль вектора скорости точки. При движении по спирали в направлении, указанном стрелкой. Радиус кривизны R увеличивается. Следовательно, при постоянной скорости v величина нормального ускорения увеличивается. 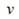 величина нормального ускорения уменьшается
величина нормального ускорения уменьшается
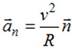
. №7 Прямолинейное движение точки описывается уравнением 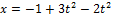 ( в единицах СИ). Средняя скорость точки за время движения до остановки в
( в единицах СИ). Средняя скорость точки за время движения до остановки в 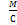 равна…
равна…
РЕШЕНИЕ
Найдем скорость: 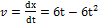 . При t =1c,
. При t =1c, 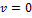 . Средняя скорость за время движения до остановки
. Средняя скорость за время движения до остановки 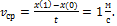 Ответ: 1
Ответ: 1 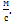
№8
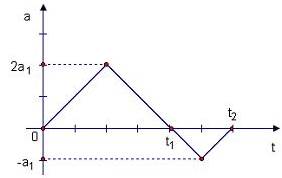
На графике показано изменение с течением времени ускорения точки на прямолинейном отрезке пути. Начальная скорость равна нулю. Скорость точки в момент времени 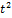 равна …
равна …
Решение.
Площадь, ограниченная графиком, представляет собой приращение скорости. За время движения 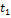 приращение скорости положительно и равно
приращение скорости положительно и равно 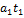 . За время
. За время 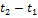 приращение скорости отрицательно и равно
приращение скорости отрицательно и равно 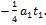 Поскольку начальная скорость равна нулю, то скорость в момент времени
Поскольку начальная скорость равна нулю, то скорость в момент времени 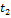 равна
равна
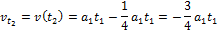
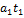
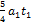
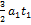
ü 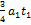
 №9
№9
Ротор электродвигателя, вращающийся со скоростью 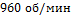 , после выключения остановился через
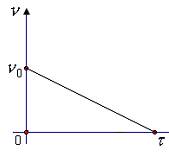
, после выключения остановился через 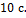 Угловое ускорение торможения ротора после выключения электродвигателя оставалось постоянным. Зависимость частоты вращения от времени торможения показана на графике. Число оборотов, которые сделал ротор до остановки, равно …
Угловое ускорение торможения ротора после выключения электродвигателя оставалось постоянным. Зависимость частоты вращения от времени торможения показана на графике. Число оборотов, которые сделал ротор до остановки, равно …
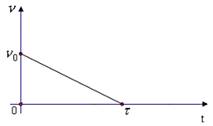 Решение.
Решение.
Начальная частота 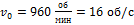 , конечна частота
, конечна частота 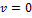 . Площадь, ограниченная графиком и осью абсцисс, равна числу оборотов, сделанных до остановки. Время
. Площадь, ограниченная графиком и осью абсцисс, равна числу оборотов, сделанных до остановки. Время 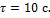 Вычисляя площадь треугольника, получим
Вычисляя площадь треугольника, получим 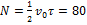 .
.
№10
Цилиндр радиуса R катится без скольжения по горизонтальной плоскости со скоростью 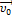 .
.
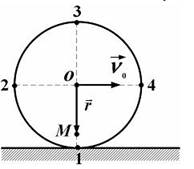
Точка М расположена на нижней половине вертикального диаметра цилиндра на расстоянии r от центра цилиндра.Зависимость мгновенной скорости точки M от расстояния до центра цилиндра имеет вид…
Решение:
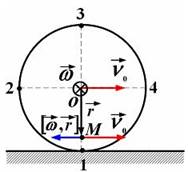 Движение точек цилиндра можно представить как результат сложения двух движений: поступательного со скоростью
Движение точек цилиндра можно представить как результат сложения двух движений: поступательного со скоростью 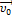 и вращательного относительно оси цилиндра с угловой скоростью
и вращательного относительно оси цилиндра с угловой скоростью 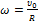 .Линейная скорость вращения относительно оси цилиндра равна
.Линейная скорость вращения относительно оси цилиндра равна 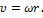
Для точек на нижней половине вертикального диаметра цилиндра эти скорости направлены противоположно. Поэтому скорость точки М равна 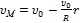 и график зависимости мгновенной скорости точки М от расстояния r до оси цилиндра имеет вид:
и график зависимости мгновенной скорости точки М от расстояния r до оси цилиндра имеет вид: 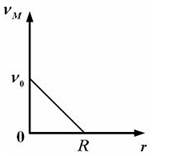
Качение цилиндра можно также представить как вращение относительно мгновенной оси вращения, которой является образующая цилиндра, касающаяся в данный момент горизонтальной плоскости.
№11
Твердое тело начинает вращаться вокруг оси z.Зависимость углового ускорения 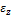 от времени t представлена на графике
от времени t представлена на графике
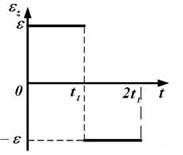
Соответствующая зависимость угловой скорости 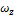 от времени представлена графиком…
от времени представлена графиком…
Решение:
Угловое ускорение характеризует быстроту изменения угловой скорости тела 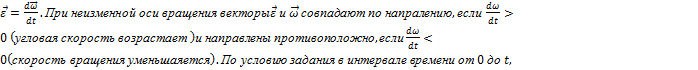
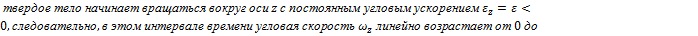
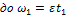 (см.рис.).В интервале времени от
(см.рис.).В интервале времени от 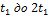 проекция углового ускорения меняет знак,
проекция углового ускорения меняет знак,
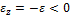 , значит, угловая скорость в этом интервале будет линейно убывать от значения
, значит, угловая скорость в этом интервале будет линейно убывать от значения 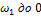 (см.рис.).
(см.рис.).
№12
Тело брошено с поверхности Земли со скоростью 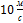 под углом 45
под углом 45 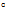 к горизонту.Если сопротивлением воздуха принебречь и принять
к горизонту.Если сопротивлением воздуха принебречь и принять 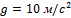 , то радиус кривизны траектории в верхней точке в м равен …
, то радиус кривизны траектории в верхней точке в м равен …
Решение:
Начальная скорость 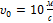 направлена под углом 45
направлена под углом 45 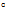 к горизонту.Проекция скорости на горизонтальное направление остается неизменой,
к горизонту.Проекция скорости на горизонтальное направление остается неизменой, 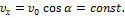 В верхней точке траектории скорость направлена горизонтально и ускорение свободного падения становится нормальным ускорением.По формуле для нормального ускорения
В верхней точке траектории скорость направлена горизонтально и ускорение свободного падения становится нормальным ускорением.По формуле для нормального ускорения 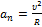 находим радиус кривизны траектории:
находим радиус кривизны траектории: 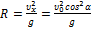 .Подставляя числовые значения, получим R=5 м.
.Подставляя числовые значения, получим R=5 м.
Тема: Работа. Энергия
№1 Частица совершила перемещение по некоторой траектории из точки 1 с радиус-вектором 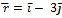 в точку 2 с радиус-вектором
в точку 2 с радиус-вектором 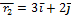 . При этом на нее действовала сила
. При этом на нее действовала сила 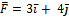 (радиус-векторы
(радиус-векторы 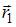 ,
, 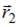 и сила
и сила 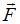 заданы в единицах СИ). Работа, совершенная силой
заданы в единицах СИ). Работа, совершенная силой 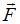 , равна … ответ: 26
, равна … ответ: 26
Решение:
По определению 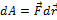 . С учетом того, что
. С учетом того, что 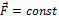 ,
,
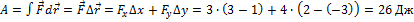
№2 На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Момент импульса первого тела
L1 = 0, 1 Дж·с. Если m = 1 кг, R = 10см, то кинетическая энергия второго тела (в мДж) равна …
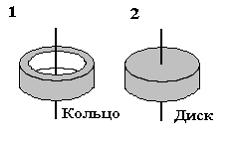 ответ: 250
ответ: 250
№3
Тело массы m=100г бросили с поверхности земли с начальной скоростью v0 = 10 м/с под углом α = 30° к горизонту. Если пренебречь сопротивлением воздуха, средняя мощность, развиваемая силой тяжести за время падения тела на землю, равна …
Ответ: 0
Решение:
Средняя мощность, развиваемая силой за некоторый промежуток времени, равна отношению работы, совершаемой силой за рассматриваемый промежуток времени, к длительности этого промежутка: 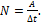 Работа силы тяжести
Работа силы тяжести 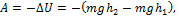 и
и 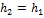 по условию задачи. Тогда A = 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, также равна нулю.
по условию задачи. Тогда A = 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, также равна нулю.
№4
Потенциальная энергия частицы задается функцией 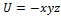 .
. 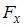 -компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна …
-компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна …
(Функция 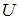 и координаты точки А заданы в единицах СИ.) Ответ: 6
и координаты точки А заданы в единицах СИ.) Ответ: 6
Решение:
Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид 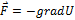 , или
, или 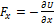 ,
, 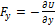 ,
, 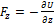 . Таким образом,
. Таким образом, 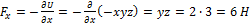 .
.
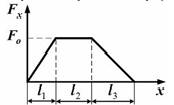 №5 Тело движется вдоль оси
№5 Тело движется вдоль оси 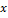 под действием силы, зависимость которой от координаты
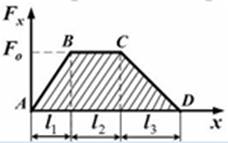
под действием силы, зависимость которой от координаты 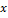 представлена на рисунке:
представлена на рисунке:
Работа силы на пути 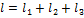 определяется выражением …
определяется выражением …
Решение:
 Работа переменной силы в случае одномерного движения на участке
Работа переменной силы в случае одномерного движения на участке 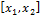 определяется как интеграл:
определяется как интеграл: 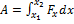 . На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту:
. На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту:
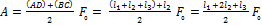 .
.

