Тема: Динамика вращательного движения.

№1

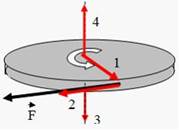Диск вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. К ободу диска приложена сила 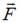, направленная по касательной.

Правильно изображает направление момента силы 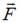вектор …

3

№2

Диск начинает вращаться вокруг неподвижной оси с постоянным угловым ускорением. Зависимость момента импульса диска от времени представлена на рисунке линией …

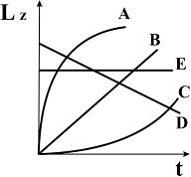
B

A

C

D

E

 

№3

Рассматриваются три тела: диск, тонкостенная труба и кольцо; причем массы m и радиусы R их оснований одинаковы.

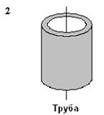
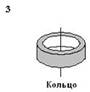
Для моментов инерции рассматриваемых тел относительно указанных осей верным является соотношение …

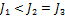
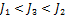
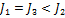
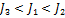
Решение:
Момент инерции сплошного однородного кругового цилиндра (диска) массы m и радиуса R относительно его оси вычисляется по формуле
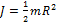, тонкостенного кругового цилиндра массы m и радиуса R относительно его оси – по формуле 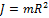. Из последней формулы видно, что момент инерции тонкостенного цилиндра (трубы, кольца) не зависит от его высоты. Поэтому правильным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение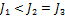

 

№4

Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил ( 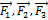или 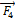), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение

 

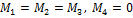
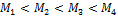
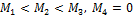
Решение:

При вращении тела вокруг неподвижной оси момент относительно этой оси создает только одна составляющая действующей на него силы, а именно касательная к траектории точки ее приложения 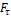. Тогда момент силы относительно неподвижной оси равен: 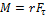, где r – радиус-вектор точки приложения силы. В данном случае составляющая 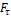одинакова для трех сил: 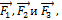а для силы 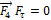. Кроме того, все силы приложены в одной точке. Поэтому .

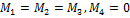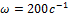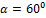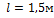№5 При выстреле орудия снаряд вылетел из ствола с угловой скоростью под углом к горизонту. Момент инерции снаряда относительно его продольной оси , расстояние между колесами орудия , время движения снаряда в стволе 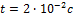время выстрела, отличаются на …

Решение:

Найдем угловые ускорения снаряда относительно продольной оси при выстреле 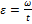. Со стороны ствола орудия на снаряд действует момент сил . По третьему закону Ньютона такой же по модулю, но противоположно направленный момент сил 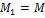действует на ствол орудия. Его проекция на горизонтальную плоскость 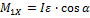уравновешивается моментом, возникающим за счет различия сил реакций опоры (давление земли), действующих на колеса, 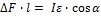, где - разность сил реакций опор. Отсюда находим . Вычисляем .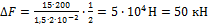

№6

При выстреле орудия снаряд вылетел из ствола с угловой скоростью

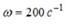под утлом 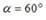к горизонту. Момент инерции снаряда относительно его продольной оси , расстояние между колесами орудия 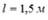, время движения снаряда в стволе 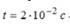Силы давления (в килоньютонах) земли, действующие на колеса во время выстрела, отличаются на...

РЕШЕНИЕ Найдем угловое ускорение вращения снаряда относительно продольной оси при выстреле 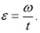Со стороны ствола на снаряд действует момент силы 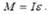По третьему закону ньютона: момент сил действует на ствол орудия. Его проекция на горизонтальную плоскость 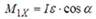уравновешивается моментом, возникающим за счет различия сил реакций опор (давления земли), действующих на колеса,

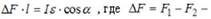разность сил реакций опор.

Отсюда находим 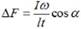. Вычисляем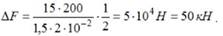

№7

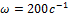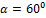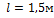При выстреле орудия снаряд вылетел из ствола с угловой скоростью под углом к горизонту. Момент инерции снаряда относительно его продольной оси , расстояние между колесами орудия , время движения снаряда в стволе 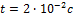время выстрела, отличаются на …

Решение:

Найдем угловые ускорения снаряда относительно продольной оси при выстреле 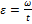. Со стороны ствола орудия на снаряд действует момент сил . По третьему закону Ньютона такой же по модулю, но противоположно направленный момент сил 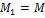действует на ствол орудия. Его проекция на горизонтальную плоскость 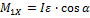уравновешивается моментом, возникающим за счет различия сил реакций опоры (давление земли), действующих на колеса, 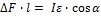, где - разность сил реакций опор. Отсюда находим . Вычисляем .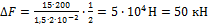

№8

Шар, цилиндр (сплошной) и тонкостенный цилиндр с равными массами и радиусами раскрутили каждый вокруг своей оси до одной и той же угловой скорости и приложили одинаковый тормозящий момент. Раньше других тел остановится …

Решение.

При одинаковом моменте сил угловое ускорение обратно пропорционально моменту инерции тела. Момент инерции шара 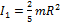, момент инерции цилиндра 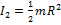, момент инерции тонкостенного цилиндра 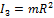. Следовательно, ускорение торможения будет большим для шара и первым остановится шар.

Цилиндр

ü Шар

Тонкостенный цилиндр цилиндр с шаром

цилиндр с шаром

№9

Величина момента импульса тела относительно неподвижной оси изменяется по закону L(t)=-1/3 t^3+4t при этом зависимость величины момента сил, действующих на тело, описывается графиком…

Решение:

Скорость изменения момента импульса относительно какой-то неподвижной оси равна величине суммарного момента внешних сил относительно этой оси, т.е. 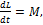где L-величина момента импульса, M –величина момента сил. Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим зависимость величины момента сил от времени .

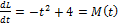Графиком этой функции является убывающая ветвь параболы.

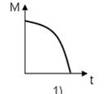
Ответ: 1)

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: