Оценивание моделей и типы зависимостей

Введение в эконометрику

Предмет эконометрики

Термин эконометрика имеет в своей основе два слова: «экономика» и «метрика».

«Метрика» от греческого слова metron – «метод расчета определения расстояния между двумя точками в пространстве». Таким образом Эконометрику можно определить как науку об экономических измерениях. Следовательно, эконометрика – это наука, которая на основе статистических данных количественно характеризует взаимозависимые экономические явления и процессы [2, 3, 5, 14].

Термин «эконометрия» (эконометрика) введен в научную литературу в 1930г норвежским статистиком Рагнаром Фришем для обозначения нового направления научных исследований.

Цель эконометрики – это количественная характеристика экономических закономерностей, выявляемых экономической теорией в общих чертах.

Задача эконометрики состоит в построении экономических моделей, оценивание их параметров, проверка гипотез о свойствах экономических показателей и формах их связи

Предмет исследования эконометрики - это массовые экономические процессы и явления.

Эконометрика как наука является следствием междисциплинарного подхода к изучению экономики и представляет собой сочетание трех наук:

-экономической теории;

-математики;

-математической и экономической статистики.

Следовательно, эконометрика с помощью статистических и математических методов анализирует экономические закономерности, доказанные экономической теорией.

Типы статистических данныx

Основу экономического моделирования составляют статистические данные, которые различают по типам: пространственным (перекрестным) и временным.

Пространственные или перекрестныеданные – это данные по каком-либо экономическому показателю, полученные от разных однотипных объектов (фирм, регионов, стран и.др.) в один момент времени (пространственный разрез). Эти данные могут быть взяты в разные моменты, если время несущественно.

Например, данные об объеме производства, количестве работников, доходов разных фирм в один и тот же момент времени.

Временные ряды – этоданные, характеризующие один и тот же объект в различные моменты времени (временные разрез)

Например, ежеквартальные данные об инфляции, средней заработной плате, данные о национальном доходе за последние годы. Отличительная черта временных данных – это упорядоченность во времени.

Промежуточное место занимают панельные данные, которые отражают наблюдение по большому числу объектов за небольшое число моментов времени.

Например, прибыли предприятий Казахстана за последние три года.

Подготовка и отбор статистических данных имеют существенное значение. Они должны быть согласованны между собой и имеет единую математическую основу. Например, не следует смешивать данные по ВВН (валовой внутренний налог) и ВНП (валовой национальный продукт), индекс потребительских цен и дефлятор ВНП и др.

Статистические данные представляются в виде таблиц, гистограмм, временных графиков и диаграмм рассеивания.

Для предоставления данных используются: таблицы, временные графики и диаграммы рассеивания.

Наблюдения дают лишь часть всевозможных реализаций случайной величины. Ее называют выборкой. Данные выборки можно предоставить в виде таблицы 1.1:

Таблица 1.1

j	x
	х₁
	x₂
…	…
n	х_n

Для таблицы 1.1 можно построить гистограмму интервалов, в которой показывают все наблюдения величины , разбиваемые на несколько промежутков одинаковой длины. Пусть числа элементов выборки, попавших в -й интервал. Тогда гистограмма это кусочно-постоянная функция, равная на -м интервале (рисунок 1.1)

Рисунок 1.1 - Гистограмма

Значительную информацию о взаимосвязи двух случайных величин x и y можно получить из диаграммы рассеяния.

Например: Таблица наблюдений двух переменных имеет вид (таблица 1.2):

Таблица 1.2

j	x	y
	x₁	y₁
	x₂	y_.
…	…	…
n	x_n	y_n

На диаграмме рассеяния отображены точками с соответствующими координатами (рисунок 1.2)

Рисунок 1.2 – Диаграмма рассеяния

Классы моделей

Основная задача эконометрики состоит в построении экономических моделей, описывающих взаимообусловленное развитие социально-экономических процессов на основе статистической информации, которая отражает распределение уровня этих процессов во времени или (и) в пространстве однородных объектов.

Выделяются три основных класса моделей:

-модели временных рядов;

-регрессионные модели с одним уравнением;

-систем одновременных уравнений.

К моделям временных рядов относятся модели тренда и модели сезонности.

Тренд представляет собой устойчивое изменение уровня показателя в течение длительного времени.

Сезонность характеризует устойчивые внутригодовые колебания уровня показателя.

Кроме того, к этому классу относятся множество более сложных моделей таких как модель адаптивного прогноза, модель - авторегрессии.

Общей чертой этого класса моделей является то, что они объясняют поведение временного ряда исходя только из предыдущих значений.

Регрессионные модели с одним уравнением имеют объясняемую переменную, которая представляется в виде функцией объясняющих переменных.

Например, модель спроса на некоторый товар в зависимости от его цены и дохода.

По виду функции регрессионные модели делятся на линейные и нелинейные. Существуют эффективные методы оценки и анализа линейных регрессионных моделей, что является базовым в прикладной эконометрике.

Область применения регрессионных моделей, даже линейных, значительно шире моделей временных рядов.

Системы одновременных уравнений описываются системами уравнений, состоящими из тождеств и регрессионных уравнений, в каждом из которых кроме объясняющих переменных содержится объясняемые переменные из других уравнений системы.

Например, модель формирования доходов.

Вышеприведенные классы моделей могут использоваться при моделировании экономических процессов. Обычно предполагают, что все факторы, не учтенные явно в экономической модели, оказывают на объект косвенно, а порой некоторые результирующие воздействия, величина которого задается случайной компонентой.

Введение случайной компоненты в экономическую модель делает ее доступной для эмпирической проверки на основе статистических данных.

Операция суммирования

Пусть величина х задается последовательностью данных х_1,х_{2, …,}х_n , каждое из которых можно записать как х_i, где i= 1, 2, …n (или ) [1, 18]

Сумма этих чисел обозначается:

, причем

Если из контекста ясно, каковы начальный и конечный суммированные члены, то используется сокращенная запись .

Сумма квадратов этих чисел обозначается:

Среднее значение величины x:

Среднее значение величины :

Имеет место неравенство:

Правила суммирования (a и b – константы)

Задача 1.1: Докажите эти правила.

Выборочная ковариация

Для изложения идей и понятий регрессионного анализа необходимо ввести понятия ковариации и корреляции [5, 15].

Различают выборочную и теоретическую ковариацию.

Выборочной ковариацией двух переменных х и у называется средняя величина произведения отклонений этих переменных от своих средних, т.е.

Или ,

где , - выборочные средние переменных х и у.

Выборочная ковариация является мерой взаимосвязи между двумя переменными.

Пусть данные наблюдений переменных х и у представлены в виде точечного графика - диаграммы рассеяния наблюдений (рисунок 3.1).

Точка на диаграмме является центром рассеяния переменных (центром тяжести совокупности точек, представляющих наблюдения).

Вертикальная и горизонтальная прямые, проведенные через точку разделяют диаграмм рассеяния на 4 области. Наблюдения в I и III областях дают положительный вклад ковариацию, а во II и IV областях - отрицательный.

Если положительные вклады преобладают над отрицательными, то ковариация будет положительной, в противном случае она будет отрицательной.

Рисунок 3.1

При положительной (прямой) связи с увеличением одной переменной другая переменная в среднем также увеличивается и наоборот при отрицательной связи.

Правила расчета ковариации.

1) .

2) Если , то .

3) , где а –const.

4) , где b-const.

5) .

Теоретической ковариацией случайных величин и называется математическое ожидание произведения отклонений этих величин от их средних значений, т.е,

где .

В записи символ означает, что рассматривается по генеральной совокупности.

Свойства теоретической ковариации:

2) если случайные величины и независимы, то

Доказательство:

Правила вычисления теоретической ковариации точно такие же, как и для выборочной ковариации.

Пример 3.1. В некоторой бюрократической стране годовой доход каждого индивида у определяется по формуле: у = 10000+500 s + 200 t, где s – число лет обучения индивида; t – трудовой стаж(в годах); х – возраст индивида. Рассчитать cov (x, y ), cov (x, s), и cov (x, t) для выборки из пяти индивидов, описанной в таблице 3.1, и проверьте, что cov(x, y) = 500cov(x, s) + 200cov(x, t).

Таблица 3.1

индивид	Возраст (годы), х	Годы обучения, s	Трудовой стаж, t	Доход, у





n=5

Объясните аналитически, почему так происходит.

Решение.

Вычислим средние значения: , , , .

Cov(x, y) = 4840

Cov(x, y) = 500 cov(x, s) +200 cov(x, t) = 500*4+200*14.2 = 4840

4840 = 4840.

Выборочная дисперсия

Пусть имеем выборку из n наблюдений

Выборочная дисперсия (вариация) определяется как среднеквадратическое отклонение в выборке

Замечание 1. Определенная таким образом выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии. Если определена как то онабудет несмещенной оценкой для (теоретической дисперсии, то есть дисперсии генеральной совокупности) отсюда следует, что ожидаемое значение величины .

Причем она имеет отрицательные смещения. Если размер выборки становится больше, то и математическое ожидание величины

Так как, является несмещенной, то ее часто определяют как выборочную дисперсию.

Правила расчета выборочной дисперсии:

1) , a – const

2) , b-const

3) , где a и b - const

4) если

5) , доказано,

Правила расчета выборочной дисперсии с помощью ковариации.

1) Если y=v+w , то

2) .

Коэффициент корреляции

Более точной мерой зависимостей между величинами является коэффициент корреляции.

Подобно дисперсии и ковариации коэффициент корреляции имеет две формы:

- выборочную;

- теоретическую.

Теоретический коэффициент корреляции определяется выражением

(3.1)

где –средние квадратические отклонения случайных величин

–теоретическая ковариация

Теоретический коэффициент корреляции показывает тесноту линейной связи двух случайных величин:

- если между переменными и существует положительная зависимость (связь) то , а следовательно ;

- если существует строгая положительная линейная зависимость, то принимает максимальное значение и .

Аналогично:

при отрицательной связи;

при строгой отрицательной зависимости;

при отсутствии линейной связи, то есть, если и независимы в этом случае теоретическая ковариация равна нулю.

Выборочный коэффициент корреляции определяется выражением:

(3.2)

Это выражение получено из выражения (3.1) путем замены теоретических дисперсий и ковариации на их несмещенные оценки. Эти оценки могут быть получены умножением выборочных дисперсий и ковариации на Следовательно,

Выборочный коэффициент корреляции является случайной величиной.

- это максимальное значение, если между выборочными значениями и строгая линейная положительная зависимость.

показывает, что зависимость между наблюдениями и в выборке отсутствует.

минимальное значение, когда существует линейная отрицательная зависимость, то есть точки лежат точно на нисходящей прямой линии.

Геометрический смысл коэффициента корреляции (рисунок 3.2 (а, б, в, г)):

в)

г)

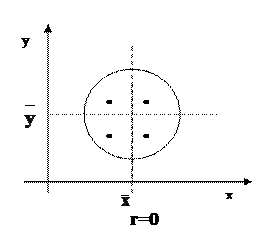
Рисунок 3.2 (а, б, в, г)

На рисунке 3.2(а, б) и случайные величины и кореллированы, на рисунке 3.2(в, г) r=0 - случайные величины зависимы, т.е случайные величины не коррелированны.

Случайные величины и называются некоррелированными, если и коррелированными если .

Свойства коэффициента корреляции.

- Eсли случайные величины и независимы, то они некоррелированные . Однако из некоррелированности не следует их независимость.

- Равенство указывает на отсутствие линейной связи между переменными, но не на отсутствие связи между ними вообще.

- Если для генеральной совокупности это необязательно означает, что для выборочной совокупности.

Контрольные вопросы:

1.Что такое выборочная, теоретическая ковариация?

2.Что такое выборочная дисперсия?

3.Какие две формы имеет коэффициент корреляции?

4.Правила расчета ковариации, дисперсии.

5. Что означает r =0.

6. Перечислите свойства коэффициентов корреляции

Парный регрессионный анализ

Задание 4.1

Докажите, что , где коэффициент корреляции между

– их стандартные отклонения.

4.3 Качество оценки: Коэффициент детерминации

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной .

Пусть на основе выборочных наблюдений построено уравнение регрессии .

Значение зависимой переменной в каждом наблюдении можно разложить на две составляющие , , где остаток есть та часть зависимой переменной , которую невозможно объяснить с помощью уравнения регрессии.

Разброс значений зависимой переменной характеризуется выборочной дисперсией . Разложим :

Так как , то .

Замечание. Такое разложение дисперсии верно лишь в том случае, когда константа а включена в уравенение регрессии.

Итак, дисперсия разложена на две части:

– часть, которая объясняется регрессионным уравнением,

– необъясненная часть.

Разделим правую и левую часть равенства на :

TSS=ESS+RSS.

Получим .

Коэффициентом детерминации называется отношение

Коэффициентом детерминации и характеризует долю дисперсии (вариации или разброса) зависимой переменной, объясненную с помощью уравнения регрессии.

Максимальное значение .

Это происходит в случае, когда все точки наблюдения лежат на регрессионной прямой (подгонка точная), т.е. и остатки для всех .

Тогда . Если , то регрессия ничего не дает, т.е. .

Это значит, что переменная не улучшает качества предсказания по сравнению с горизонтальной прямой (рисунок 4.5).

Рисунок 4.5

Чем ближе к единице , тем лучше качество подгонки, т.е. более точно аппроксимирует .

Замечание. Вычисление корректно, если константа а включена в уравнение регрессии.

Напомню, что выборочные дисперсии и :

дисперсия наблюдаемых значений .

дисперсия расчетных значений

- дисперсия остатков.

Пример 4.1 Изучается зависимость себестоимости единицы изделия (у, тыс. руб.) от величины выпуска продукции (х, тыс. шт.) по группам предприятий за отчетный период. Экономист обследовал n = 5 предприятий и получил следующие результаты (1-й и 2-й столбцы). Полагая, что между переменными х, у имеет место линейная зависимость, определим выборочное уравнение линейной регрессии. Заполним таблицу

Номер	х	у	х²	х*у
		1.9		3.8
		1.7		5.1
		1.8		7.2
		1.6		8.0
		1.4		8.4
n = 5
Сред нее

Уравнение линейной регрессии имеет вид:

Найдем остатки и коэффициент детерминации.

Решение: Заполним таблицу

Но мер	х	y	y²	=2.12- -0.11x
		1, 9	3, 61	1, 90	0, 00	0, 22	0, 22	0, 0484	0.0484
		1, 7	2, 89	1, 79	-0, 09	0, 02	0, 11	0, 0004	0.0121	0.0081
		1, 8	3, 24	1, 68	0, 12	0, 12		0, 0144		0.0144
		1, 6	2, 56	1, 57	0, 03	-0, 08	-0, 11	0, 0064	0.0121	0.0009
		1, 4	1, 96	1, 46	-0, 06	-0, 28	-0, 22	0, 0784	0.0484	0.0036
Сумма		8, 4	14, 26					0, 148	0.121	0.027
Сред ние								0, 0296=var(y)	0.0242= var( )	0.0054=var( )

var(y)= ; var( )= ; var( )=

Проверим: Var(y)=var( )+var( ); 0.0296=0.0242+0.0054

0.0296=0.0296, отсюда R²=

Т.е. 81, 7 % общей вариации себестоимости у зависит от выпуска продукции х. Наша модель не объясняет 18, 3 % вариации себестоимости. Эта часть вариации объясняется факторами, не включенными в модель.

Пример 4.2. Показать, что , где - коэффициент корреляции между и .