Вероятность в непрерывном случае

Дискретные случайные величины принимают значение из некоторого конечного набора. Каждое из этих значений связано с определенной вероятностью, характеризующей его «вес». Если эти «веса» известны, то всегда можно рассчитать теоретическое среднее (математическое ожидание) и дисперсию [5].

Представим указанные «веса» как определенные количества «пластической массы», равные вероятностям соответствующих значений, тогда как сумма вероятностей равна единице, то и суммарный «вес» этой массы равен единице.

Например, пусть величина х есть сумма очков, выпавших при бросании двух игральных костей. Величина х принимает значение от 2 до 12 и для всех этих значений количество соответствующей массы можно показать в виде гистограммы (рисунок 1.6)

Рисунок 1.6

Непрерывные случайные величины могут принимать бесконечное число значений. В этом случае представить себе «пластическую массу» разделенную на бесконечное число частей практически невозможно. Поэтому для непрерывных случайных величин используются другие подходы.

Например, пусть температура в комнате меняется в пределах от 55 до 75′ по Фаренгейту. Вначале, допустим, что все значения в этом диапазоне равновероятны. Поскольку число различных значений принимаемых показателем температуры, бесконечно, то пытаться разделить «пластическую массу» на малые части бессмысленно. Вместо этого «размножим» ее по всему диапазону.

По предположению все температуры от 55 до 75′ равновероятны, тогда масса должна быть «размазана» равномерно, что и покажем на рисунке 1.7:

Температура, F

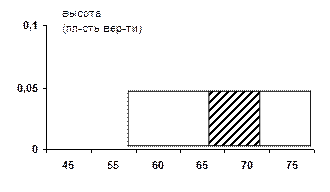
Рисунок 1.7

Известно, что совокупная вероятность всегда равна единице, тогда положим, что «пластическая масса размазана» на единичной площади. В данном случае «масса» покрыла прямоугольник. Основание прямоугольника равно а=75-55=20, высоту h определим из соотношения .

Найдя высоту прямоугольника можно ответить на вопросы типа:

- с какой вероятностью температура будет находится в диапазоне например от 65° до 70° F. Ответ определяется величиной замазанной площади, лежащей в диапазоне от 65° до 70° F, которую заштрихуем. Основание заштрихованного прямоугольника равно 70-65 = 5, высота 0, 05, тогда площадь равно 5*0, 05=0, 25. промежуток от 65° до 75° F составляет ¼ всего диапазона, следовательно искомая вероятность равна .

Высота заштрихованной площади представляет то, что формально называется плотностью вероятности в той точке. Если эта высота может быть записана как функция значений случайной переменной, то эта функция называется функцией плотности вероятности.

В нашем примере она записывается как , где х - температура тогда если , то ƒ (х)=0, 05

В качестве первого приближений функция плотностью вероятности показывает вероятность нахождения случайной переменной внутри единичного интервала вокруг данной точки.

В нашем примере ƒ (х) =0, 05 всюду, следовательно, температура находится, например между 60⁰ и 61⁰ F с вероятностью 0, 05.

В нашем случае график функции плотности вероятности горизонтален и ее указанная интерпретация точка.

В общем случае эта функция непрерывно меняется и ее интерпретация дает лишь приближение. Рассмотрим пример, когда эта функция непостоянна, поскольку не все температуры равновероятны.

Пример 1.9. Предположим, что центральное отопление работает таким образом, что температура никогда не падает ниже 65 F. В жаркие дни температура превосходит этот уровень не превшая 75F. Будем считать, что плотность вероятности максимальна при t°=65′ F и далее она равномерно убывает до нуля при t°=75′ F. Совокупная вероятность равна единице, тогда общая «заштрихованная» площадь равна единице (рисунок 1.8).

Рисунок 1.8

Площадь треугольника равна половине произведения основания на высоту: высота равна 0, 2, основание 76⁰-65⁰=10, тогда площадь равна .

Предположим, что нужно вычислить вероятность нахождения температуры в промежутке между 65F и 75F (она заштрихована дважды)

Для этого вычислим вероятность нахождения температуры в диапазоне

70⁰-75⁰F. Это так же площадь треугольника с основанием 75⁰-70⁰=5 и высотой 0, 1, следовательно , то есть вероятность попадания температуры в диапазоне 70⁰-75⁰ F равна 0, 25 или 25%.

Тогда с вероятностью 1-0, 25=0, 75 или 75% температура попадает в диапазон 65⁰-75⁰F.

 

Контрольные вопросы:

1. Дать определение эконометрике.

2. Какие задачи ставятся в эконометрике?

3. Перечислите типы статистических данных.

4. Какие классы моделей встречаются в эконометрике?

5. Перечислите правила суммирования.

6. Какую переменную называют случайной?

7.Перечислите свойства функции распределения.

8. Дать определение дискретной и непрерывной случайной переменной.

9. Как определяется вероятность в непрерывном случае?

10. Как определяется математическое ожидание дискретной случайной величины?

⇐ Предыдущая12345678Следующая ⇒

Поделиться: