Выборочная ковариация. Выборочная дисперсия. Коэффициент корреляции

Выборочная ковариация

Для изложения идей и понятий регрессионного анализа необходимо ввести понятия ковариации и корреляции [5, 15].

Различают выборочную и теоретическую ковариацию.

Выборочной ковариацией двух переменных х и у называется средняя величина произведения отклонений этих переменных от своих средних, т.е.

Или ,

где , - выборочные средние переменных х и у.

Выборочная ковариация является мерой взаимосвязи между двумя переменными.

Пусть данные наблюдений переменных х и у представлены в виде точечного графика - диаграммы рассеяния наблюдений (рисунок 3.1).

Точка на диаграмме является центром рассеяния переменных (центром тяжести совокупности точек, представляющих наблюдения).

Вертикальная и горизонтальная прямые, проведенные через точку разделяют диаграмм рассеяния на 4 области. Наблюдения в I и III областях дают положительный вклад ковариацию, а во II и IV областях - отрицательный.

Если положительные вклады преобладают над отрицательными, то ковариация будет положительной, в противном случае она будет отрицательной.

 

Рисунок 3.1

При положительной (прямой) связи с увеличением одной переменной другая переменная в среднем также увеличивается и наоборот при отрицательной связи.

Правила расчета ковариации.

1) .

2) Если , то .

3) , где а –const.

4) , где b-const.

5) .

Теоретической ковариацией случайных величин и называется математическое ожидание произведения отклонений этих величин от их средних значений, т.е,

,

где .

В записи символ означает, что рассматривается по генеральной совокупности.

Свойства теоретической ковариации:

1)

2) если случайные величины и независимы, то

Доказательство:

Правила вычисления теоретической ковариации точно такие же, как и для выборочной ковариации.

Пример 3.1. В некоторой бюрократической стране годовой доход каждого индивида у определяется по формуле: у = 10000+500 s + 200 t, где s – число лет обучения индивида; t – трудовой стаж(в годах); х – возраст индивида. Рассчитать cov (x, y ), cov (x, s), и cov (x, t) для выборки из пяти индивидов, описанной в таблице 3.1, и проверьте, что cov(x, y) = 500cov(x, s) + 200cov(x, t).

Таблица 3.1

индивид	Возраст (годы), х	Годы обучения, s	Трудовой стаж, t	Доход, у
n=5

Объясните аналитически, почему так происходит.

Решение.

Вычислим средние значения: , , , .

Cov(x, y) = 4840

Cov(x, y) = 500 cov(x, s) +200 cov(x, t) = 500*4+200*14.2 = 4840

4840 = 4840.

 

Выборочная дисперсия

Пусть имеем выборку из n наблюдений

Выборочная дисперсия (вариация) определяется как среднеквадратическое отклонение в выборке

Замечание 1. Определенная таким образом выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии. Если определена как то онабудет несмещенной оценкой для (теоретической дисперсии, то есть дисперсии генеральной совокупности) отсюда следует, что ожидаемое значение величины .

Причем она имеет отрицательные смещения. Если размер выборки становится больше, то и математическое ожидание величины

Так как, является несмещенной, то ее часто определяют как выборочную дисперсию.

Правила расчета выборочной дисперсии:

1) , a – const

2) , b-const

3) , где a и b - const

4) если

5) , доказано,

6)

Правила расчета выборочной дисперсии с помощью ковариации.

1) Если y=v+w , то

2) .

Коэффициент корреляции

Более точной мерой зависимостей между величинами является коэффициент корреляции.

Подобно дисперсии и ковариации коэффициент корреляции имеет две формы:

- выборочную;

- теоретическую.

Теоретический коэффициент корреляции определяется выражением

(3.1)

где –средние квадратические отклонения случайных величин

–теоретическая ковариация

Теоретический коэффициент корреляции показывает тесноту линейной связи двух случайных величин:

- если между переменными и существует положительная зависимость (связь) то , а следовательно ;

- если существует строгая положительная линейная зависимость, то принимает максимальное значение и .

Аналогично:

при отрицательной связи;

при строгой отрицательной зависимости;

при отсутствии линейной связи, то есть, если и независимы в этом случае теоретическая ковариация равна нулю.

Выборочный коэффициент корреляции определяется выражением:

(3.2)

Это выражение получено из выражения (3.1) путем замены теоретических дисперсий и ковариации на их несмещенные оценки. Эти оценки могут быть получены умножением выборочных дисперсий и ковариации на Следовательно,

.

Выборочный коэффициент корреляции является случайной величиной.

- это максимальное значение, если между выборочными значениями и строгая линейная положительная зависимость.

показывает, что зависимость между наблюдениями и в выборке отсутствует.

минимальное значение, когда существует линейная отрицательная зависимость, то есть точки лежат точно на нисходящей прямой линии.

Геометрический смысл коэффициента корреляции (рисунок 3.2 (а, б, в, г)):

в)

г)

 

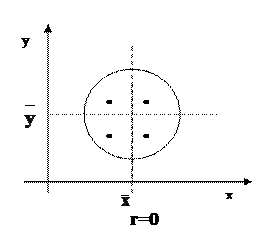
Рисунок 3.2 (а, б, в, г)

На рисунке 3.2(а, б) и случайные величины и кореллированы, на рисунке 3.2(в, г) r=0 - случайные величины зависимы, т.е случайные величины не коррелированны.

Случайные величины и называются некоррелированными, если и коррелированными если .

Свойства коэффициента корреляции.

- Eсли случайные величины и независимы, то они некоррелированные . Однако из некоррелированности не следует их независимость.

- Равенство указывает на отсутствие линейной связи между переменными, но не на отсутствие связи между ними вообще.

- Если для генеральной совокупности это необязательно означает, что для выборочной совокупности.

 

Контрольные вопросы:

1.Что такое выборочная, теоретическая ковариация?

2.Что такое выборочная дисперсия?

3.Какие две формы имеет коэффициент корреляции?

4.Правила расчета ковариации, дисперсии.

5. Что означает r =0.

6. Перечислите свойства коэффициентов корреляции

 

 

Парный регрессионный анализ

⇐ Предыдущая12345678Следующая ⇒

Поделиться: