АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА В ВЕТВИ, СОДЕРЖАЩЕЙ РЕЗИСТОР, КАТУШКУ ИНДУКТИВНОСТИ И КОНДЕНСАТОР, ПРИ ПОДКЛЮЧЕНИИ ЕЕ К ИСТОЧНИКУ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ

Пусть контур - цепи подключен к источнику синусоидального напряжения (рис. 3.10).

Докоммутационный режим: ; .

Послекоммутационный режим: ,

где

Поскольку входное сопротивление будет такое же, что и при подключении к источнику постоянного тока, то их характеристическое уравнение, и его корни будут теми же.

Для определения постоянных интегрирования записываем систему уравнений (3.22) для

Слагаемые этих уравнений уточняются из законов коммутации

Из второго закона Кирхгофа имеем

откуда

С другой стороны, или

Система уравнений для имеет вид:

(3.25)

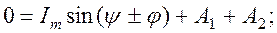
Совместное решение позволяет определить постоянные интегрирования

;

Окончательное выражение тока переходного процесса будет

(3.26)

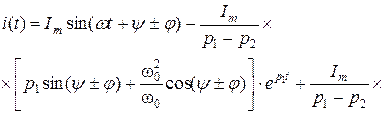
Характер изменения тока переходного процесса складывается из наложения принужденной и свободной составляющих тока.

Свободная составляющая зависит от соотношения между параметрами ветви и может приобретать как апериодический процесс при (рис. 3.11, а), так и периодический затухающий процесс при (рис. 3.11, б).

Амплитудные значения тока и напряжения на конденсаторе зависят от соотношения между угловой частотой незатухающих колебаний .

Если угловая частота , то независимо от момента включения при переходной процесс может сопровождаться значительными бросками тока. Напряжение на емкости в этом случае не превышает удвоенной амплитуды напряжения на ней при установившемся режиме. Если угловая частота , то в момент включения, когда , то переходной процесс сопровождается током, амплитуда которого не превышает амплитуды тока установившегося режима более чем в два раза, а переходное напряжение на емкости при этом может достичь значительной величины.

3.7 ВКЛЮЧЕНИЕ rLC – ЦЕПИ СО СЛАБЫМ ЗАТУХАНИЕМ НА ГАРМОНИЧЕСКОЕ НАПРЯЖЕНИЕ

Пусть к - цепи рисунок 3.7 с добротностью подключен источник синусоидального напряжения

В установившемся режиме напряжение на емкости , есть принужденная составляющая, где - начальная фаза емкостного напряжения.

Общее решение переходного напряжения на емкости представлено суммой принужденной и свободной составляющих

(3.27)

Для определения в уравнении и необходимо составить еще одно уравнение

Подставим в оба уравнения и приводим к начальным условиям

(3.28)

(3.29)

Из уравнения (3.28) имеем

Подставляем полученное выражение в уравнение (3.29) и решаем его относительно .

В результате решения имеем

(3.30)

С учетом общее решение уравнения (3.27) имеет вид

(3.31)

График изменения напряжения показан на рисунке 3.12.

Напряжение начинается с нуля, амплитуда его увеличивается от периода к периоду. Для приведенного примера (рис. 3.12) пятый период близок к установившемуся синусоидальному напряжению.

Рис. 3.12

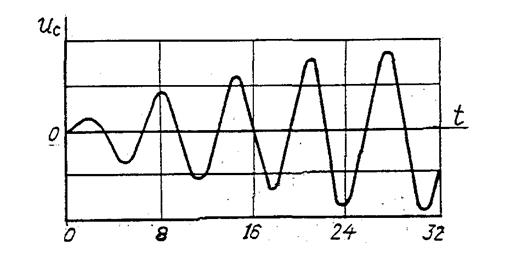
Можно выделить случай для контуров с высокой добротностью; у них , частота затухающих колебаний равна резонансной. Если частота входного напряжения близка к , то (смотри формулу (3.30)) и

переходное напряжение превращается в разность двух синусоид с одинаковыми амплитудами

(3.32)

Амплитуды напряжений увеличиваются и затем уменьшаются, то есть образуются биения.

На рисунке 3.13 представлены кривые биений для напряжения .

Угловая частота колебаний равна средней частоте

Образование биений поясняется с помощью вращающихся векторов (рис. 3.14, а). Пусть один из них, например (помеченный точкой), соответствует первому слагаемому в выражении (3.32) и вращается с угловой частотой .

Рис. 3.13

Вектор - соответствует второму слагаемому, и он вращается вдвое медленнее. За некоторое время один вектор повернется на , а второй – только на (рис. 3.14, б-г).

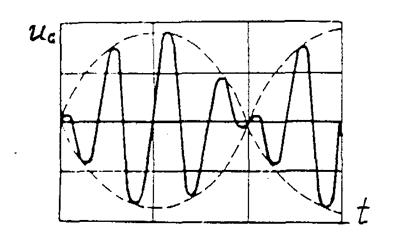
Длина результирующего вектора увеличивается от позиции к

позиции и достигает максимума, когда составляющие совпадают по направлению (рис. 3.14, д). Наибольшая амплитуда равна , затем она уменьшается до нуля.

Рис. 3.14

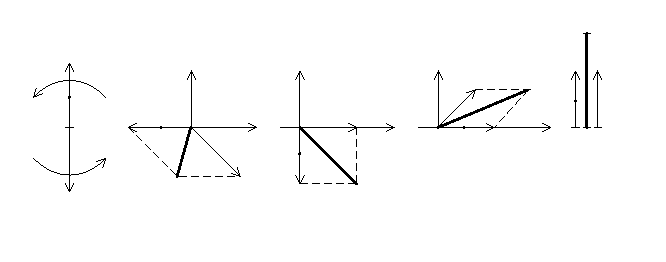
Поскольку затухание в цепи имеет место, свободные напряжения и токи затухают, биения постепенно прекращаются и переходной режим сменяется установившимся.

ПРИМЕРЫ АНАЛИЗА ПЕРЕХОДНОГО ПРОЦЕССА КЛАССИЧЕСКИМ МЕТОДОМ

ПРИМЕР 4.1

Пусть для рассматриваемого примера (рис.1.1) входное напряжение источника энергии – постоянное .

Параметры цепи Ом; Ом; Ом; Ф; Гн; Ом.

Определить переходные токи в ветвях электрической цепи и вычертить кривые изменения их во времени .

Решение

Найдем начальные условия в докоммутационной цепи (рис.1.1)

Ток в ветви с индуктивностью

А.

Напряжение на зажимах конденсатора

В.

В соответствии с законами коммутации имеем

и .

Следовательно, в послекоммутационной цепи (рис.1.1) начальные условия будут следующие:

А; В;

А;

Рис. 4.1

А.

Из схемы рисунка 4.1 определим принужденные ппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппппрррррррр

составляющие токов

А; .

Так как свободный ток есть та составляющая, которая накладываясь на принужденный ток, создает переходной ток, то значения свободных составляющих при определяются как

А;

А.

Найдем значения производных от свободных составляющих токов для момента времени .

Из второго уравнения системы 1.12 имеем

Подставив значения токов и в приведенное уравнение, будем иметь

Продифференцируем третье уравнение системы 1.12, будем иметь

откуда

А/с.

Из первого уравнения системы 7.12 имеем

А/с.

Корни характеристического уравнения определяются из выражения

После подстановки параметров цепи найдем

1/с.; 1/с.

Функции переходных токов для цепи рисунка 1.1 запишутся в виде

Подставляя в уравнения токов значения будем иметь:

А;

А.

Расчеты, необходимые для построения графиков, сводятся в таблицу 4.1

Графики зависимости переходных токов от времени изображаются кривыми, показанными на рисунке 4.2.

Таблица 4.1

, с
, А	1, 86	2, 04	2, 2	2, 21	2, 23	2, 24	2, 24
, А	2, 49	2, 02	2, 15	2, 18	2, 21	2, 23	2, 235
, А	-0, 63	0, 02	0, 05	0, 03	0, 02	0, 01	0, 005

Рис. 4.2

ПРИМЕР 4.2

Определить переходные токи в ветвях цепи рисунка 1.1 при условии, когда Ом; Ом; Ом;

Ом; Гн; Ф; В.

Решение

Корни характеристического уравнения цепи находятся из уравнения 1.15 и получаются комплексно - сопряженные

или ;

Начальные условия определяются из схемы рисунка 1.1

А;

В;

А;

Принужденные токи в послекоммутационной цепи

А;

Значения токов свободных составляющих при

А;

А.

Из уравнения находим производную

Из уравнения для второго контура находим производную второго тока

А/с.

Из уравнения, записанного по первому закону Кирхгофа, имеем

А/с.

Как известно из математики, решение дифференциального уравнения при комплексных корнях для любого тока определяется по формуле (1.18) и будет иметь вид

Значения и определяются из начальных условий. Так как неизвестных две, то имеющееся уравнение дополняется вторым уравнением, полученным путем взятия производной от первого уравнения