Приближение данных функциями

 

При моделировании систем достаточно часто приходится осуществлять приближения данных, заданных таблично, непрерывными функциями. Такие задачи возникают, например, при моделировании систем управления для нестационарных моделей объектов (моделей движения самолета на взлете и посадке, движения судна при изменении курса и т.д.). Основными методами, которые используются для построения приближающих функций, являются интерполирование алгебраическими многочленами, сплайн-функции, метод наименьших квадратов.

Интерполирование

 

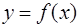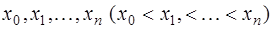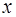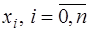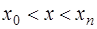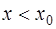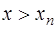Пусть задана таблица значений неизвестной функции  в точках , и необходимо определить значение этой функции в некоторой точке , не совпадающей с . Это типичная постановка задач интерполяции (если ) или экстраполяции (если  или ). Точки  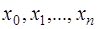называются узлами интерполирования.

В математике под интерполированием понимается задача нахождения неизвестного значения какой-либо величины по нескольким известным ее значениям и, может быть, по нескольким значениям других величин, с нею связанных (например, ее производных). Без дополнительных предположений о функции 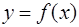 эта задача является неопределенной и за  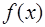можно принять любое число, если только  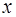не является одним из узлов таблицы.

Предположим, что рассматривается множество 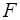 функций 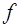, обладающих некоторыми свойствами. Рассмотрим семейство функций 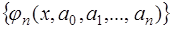, определенных на интервале 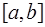, содержащем все узлы интерполирования, и зависящих от параметров 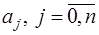. Будем полагать, что

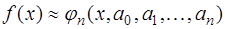.             (7.2.1)

Относительно функций 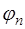 известны следующие предположения:

1) функции известны при всяких 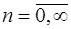 и определены на отрезке  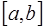для любых значений параметров ;

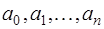2) с увеличением 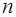 семейство функций  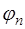расширяется;

3) при всяком 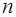 функции семейства  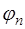обладают теми же свойствами, что и функции ;

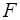4) для всякой функции 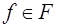 и любого числа  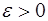существует такое  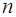и такие значения параметров 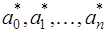, что при всех  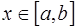выполняется неравенство:

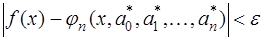
(это условие обеспечивает возможность равномерного на 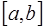 сколь угодно точного приближения любой функции  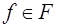с помощью функций из последовательности семейств 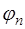, при этом семейство функций  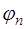называется полным для множества );

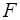5) параметры 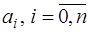 выбираются из условия совпадения функци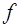й  и 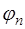 в узлах 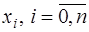. Это приводит к системе уравнений:

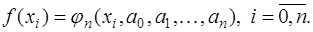            (7.2.2)

Если 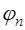 - нелинейная функция относительно 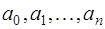, то система (7.2.2) будет нелинейной и ее решение может быть только приближенным. Поэтому чаще всего задают функцию  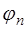линейной относительно параметров 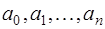, то есть в виде:

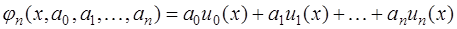, (7.2.3)

где 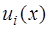,  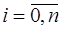- линейно независимые координатные функции, определенные на 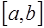. При этом система (7.2.2) примет вид:

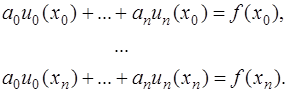           (7.2.4)

Система (7.2.4) имеет единственное решение тогда и только тогда, когда ее определитель

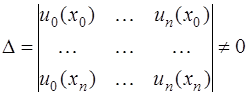.       (7.2.5)

Последовательности функций 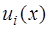, , 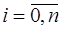для которых определитель (7.2.5) отличен от нуля при всяких несовпадающих значениях 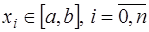, называются последовательностями Чебышева.

Часто в качестве функций 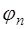 используются алгебраические многочлены:

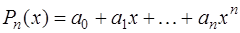.              (7.2.6)

Система (7.2.4) в этом случае имеет вид:

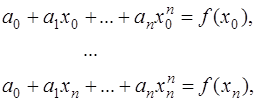              (7.2.7)

а ее определитель является определителем Вандермонда

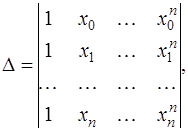
который отличен от нуля для любых несовпадающих узлов 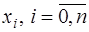. Таким образом, система (7.2.7) имеет единственное решение и интерполирование функции  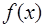по ее значениям в узлах  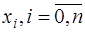с помощью многочлена  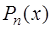всегда возможно и единственно. Кроме того, согласно теореме Вейерштрасса, если отрезок  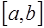конечный и замкнутый и функция  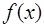непрерывна на нем вместе с производными первых  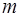порядков, то для всякого  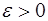существует алгебраический многочлен  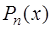некоторой степени 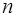, для которого при любых  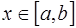выполняются неравенства

.

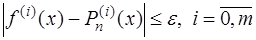Таким образом, если удачно расположить узлы на 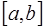, то можно получить достаточно хорошие результаты при вычислении значений функции  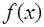и ее производных в любой точке отрезка .

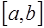Решим систему (7.2.7) по правилу Крамера. Тогда

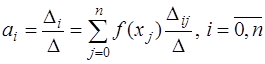,          (7.2.8)

где 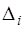 - определитель, полученный из  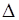заменой 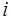-го столбца столбцом свободных членов,  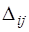- алгебраическое дополнение для 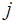-го элемента в  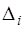при разложении по элементам 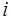-го столбца.

Найденные таким образом параметры 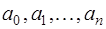 подставим в (7.2.6), приведем подобные относительно  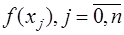и получим:

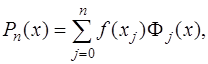                     (7.2.9)

где 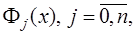 - алгебраические многочлены 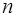-ой степени. Учитывая условие совпадения  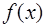и 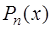 в узлах интерполирования 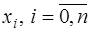, получим:

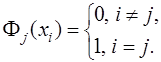
Таким образом, 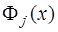 есть многочлен 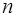-ой степени, равной нулю в  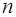точках 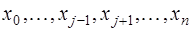, и, следовательно, представимый в виде:

.

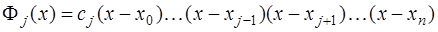Константу 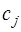 определим из условия

.

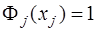Тогда

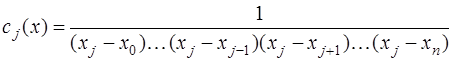
и

.

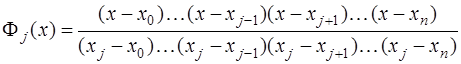Таким образом получим функцию, которая называется интерполяционным многочленом Лагранжа и обозначается :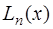

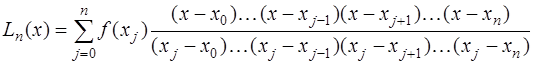. (7.2.10)

Обозначим через 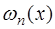 многочлен 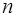-ой степени вида:

.

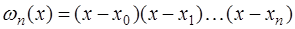Тогда многочлен Лагранжа запишется в виде:

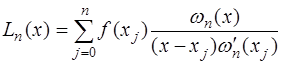.         (7.2.11)

Интерполяция многочленом Лагранжа имеет существенный недостаток: если выяснится, что полученная точность интерполирования недостаточна и для улучшения точности потребуется увеличить число узлов, то все вычисления придется проделать заново. От этого недостатка избавлен другой интерполяционный многочлен – многочлен Ньютона.

Введем следующие обозначения: разностными отношениями первого порядка назовем величины

,

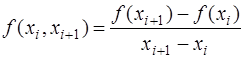разностными отношениями второго порядка -

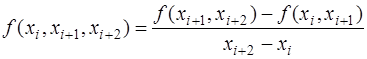
и т.д., и разностными отношениями 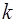-го порядка -

.

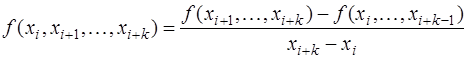Разностные отношения являются симметрическими функциями своих аргументов и

.

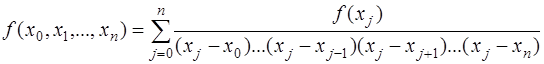Для построения многочлена Ньютона запишем многочлен Лагранжа 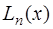 следующим образом:

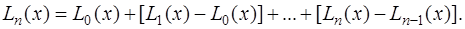(7.2.12)

Разность 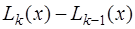 есть многочлен 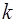-ой степени, равный нулю в точках 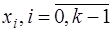, и, следовательно, представимый в виде:

.

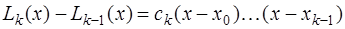Константу 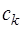 определим, полагая 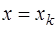, и учитывая, что 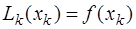, то есть

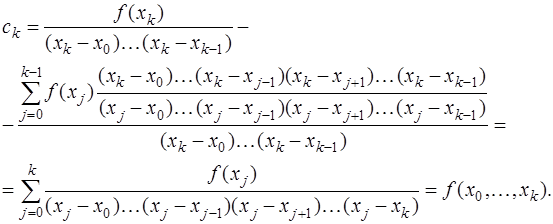
Тогда

.

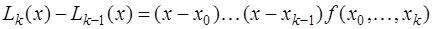Подставляя полученное выражение в (7.2.12) для 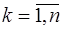, получим интерполяционный многочлен Ньютона:

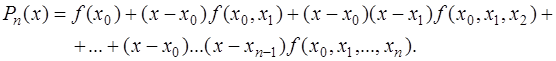(7.2.13)

Несмотря на более сложное строение, формула Ньютона удобнее для вычислений, чем формула Лагранжа, так как позволяет не фиксировать заранее число узлов, а подключать новые узлы до тех пор, пока не будет достигнута требуемая точность вычислений.

Величина остатка или погрешности интерполирования

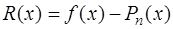                (7.2.14)

зависит от свойств функции 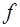, выбора узлов  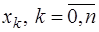и от положения точки  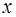на 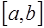. Формула Лагранжа для погрешности интерполирования  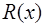имеет вид:

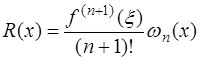,               (7.2.15)

где 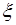 - некоторая точка отрезка 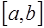. Если обозначить

,

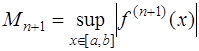то

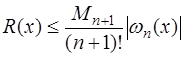.                 (7.2.16)

Для того, чтобы погрешность в (7.2.16) была наименьшей, необходимо выбрать узлы интерполирования таким образом, чтобы значение 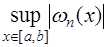 было минимальным. Для этого можно воспользоваться многочленами Чебышева:

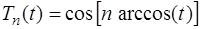.                  (7.2.17)

Многочлены Чебышева обладают следующими свойствами:

1) они являются алгебраическими многочленами соответствующей степени, так как 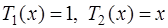, а для построения многочленов более высокой степени можно воспользоваться рекуррентной формулой:

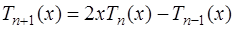;           (7.2.18)

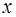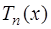2) коэффициент при старшей степени  в  равен ;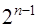

3) области определения и изменения многочленов Чебышева равны ;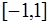

4) многочлены 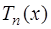 имеют 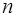 корней на 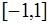, которые располагаются в точках

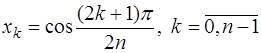;      (7.2.19)

5) многочлены 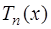 достигают  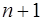экстремум, равный 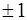, на 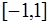 в точках

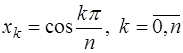;                (7.2.20)

6) они являются четными или нечетными в зависимости от 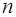, так как

;

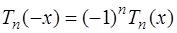7) многочлены Чебышева ортогональны с весом 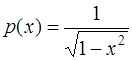 на 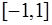, так как

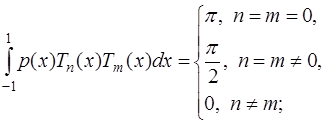
8) графическое представление многочленов Чебышева совпадает с проекциями синусов, нанесенных на цилиндр;

9) многочлены Чебышева являются наименее отклоняющимися от нуля, так как

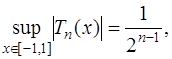
при этом справедливо утверждение, что какой бы другой многочлен 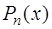 степени  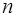со старшим коэффициентом, равным единице, мы ни взяли

.

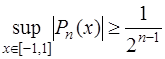Таким образом, для того чтобы значение 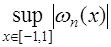 было наименьшим, необходимо в качестве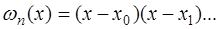 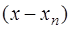 взять приведенный многочлен Чебышева 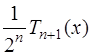, то есть в качестве узлов интерполирования взять корни многочлена Чебышева:

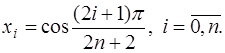          (7.2.21)

Тогда для оценки погрешности будет верно неравенство:

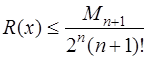.                   (7.2.22)

Если интерполирование производится на интервале 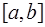, то значения  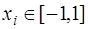с помощью линейного преобразования

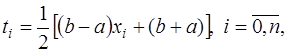       (7.2.23)

можно перевести в интервал 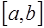, а для оценки погрешности будет верно неравенство:

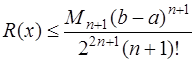.                    (7.2.24)

Достаточно часто при интерполировании приходится иметь дело с равноотстоящими узлами. Тогда полагают:

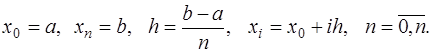
В этом случае интерполяционные формулы можно значительно упростить, если ввести понятие конечных разностей.

Конечной разностью 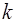-го порядка называется величина

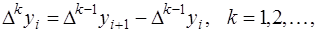
где

.

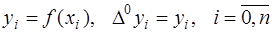Так как узлы, лежащие вблизи точки интерполирования 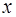, оказывают большее влияние, чем узлы, лежащие дальше, то целесообразно при построении интерполяционной формулы привлекать сначала ближний узел, а затем остальные в порядке их удаленности от точки 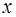. При этом абсолютные величины слагаемых будут уменьшаться с увеличением их порядкового номера и, начиная с некоторого слагаемого, выйдут за пределы требуемой точности. В соответствии с этим построим конкретные интерполяционные формулы.

 

Формула Ньютона для интерполирования вперед

Пусть точка 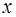 находится ближе к левому концу отрезка  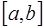или слева от него. Для построения интерполяционной формулы Ньютона за  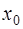принимается ближайший к  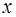узел интерполирования, а затем узлы привлекаются в следующем порядке:

         ,

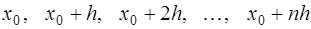при этом, если это возможно, за 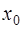 выбирается лежащий слева от точки  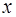узел, чтобы не попасть в ситуацию экстраполирования. Тогда многочлен Ньютона (7.2.13) запишется в виде:

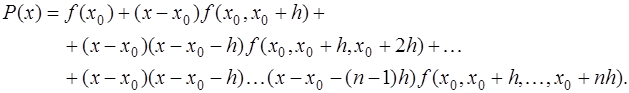
Если ввести новую переменную 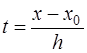, то

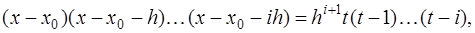
и учитывая, что

,

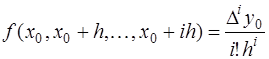получим

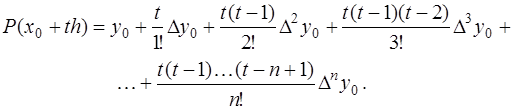(7.2.25)

Эта формула называется формулой Ньютона для интерполирования вперед.

 

Формула Ньютона для интерполирования назад

Пусть точка  находится ближе к правому концу отрезка  или справа от него. За первый узел для построения интерполяционной формулы примем ближайший к 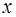 узел интерполирования и обозначим его 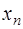, при этом, если возможно, следует избегать ситуации экстраполирования. Далее узлы для построения интерполяционной формулы следует привлекать в следующем порядке:

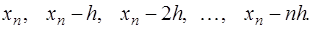
Введем новую переменную 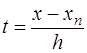. Тогда, преобразовывая аналогично предыдущему, получим формулу Ньютона для интерполирования назад:

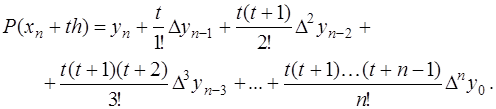(7.2.26)

 

Интерполяционные формулы Гаусса

Если точка интерполирования 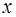 находится в середине отрезка  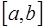вблизи узла 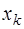, причем правее его, то есть 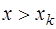, то узлы привлекаются в следующем порядке:

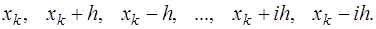
Тогда, после введения новой переменной 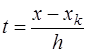 и соответствующих преобразований, получается формула Гаусса для интерполирования вперед, которая имеет вид:

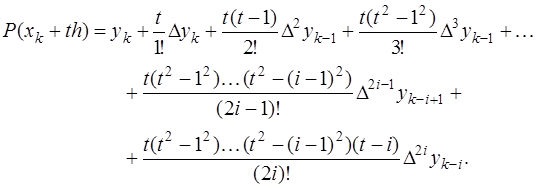 (7.2.27)

Если точка 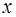 находится вблизи узла 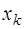, причем 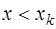, то для построения интерполяционной формулы узлы привлекаются в следующем порядке:

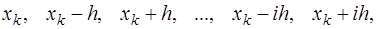
и, после введения переменной 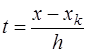 и соответствующих преобразований, получим формулу Гаусса для интерполирования назад:

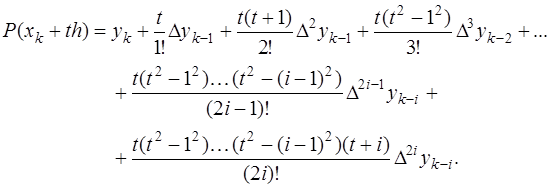(7.2.28)

Если функция 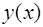 достаточно гладкая, то разности  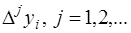убывают с ростом  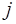и для некоторого  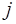они практически равны нулю. Но, так как с ростом порядка разностей растет погрешность их вычисления, то привлечение таких разностей для построения интерполяционной формулы может существенно исказить результат. Существует следующее правило определения максимального порядка разностей, которые ведут себя правильно, то есть не вносят дополнительной погрешности в значение интерполяционного многочлена.

Пусть значения 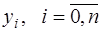 вычислены с абсолютной погрешностью 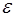. Так как конечные разности определяются по формуле:

,

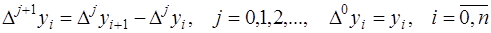то абсолютная погрешность разностей первого порядка равна 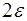, второго порядка – 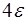,…, 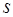-го порядка – 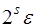. Тогда, если

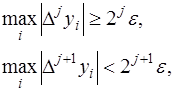
то максимальный порядок разностей, которые ведут себя правильно, равен 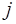. Разности 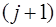-го порядка уже меньше погрешности, поэтому их использование приведет к искажению результата и при построении интерполяционной формулы они отбрасываются.

Сплайн-функции

 

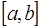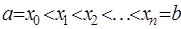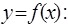
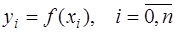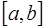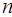Пусть на отрезке  задано разбиение , в узлах которого известны значения достаточно гладкой функции . Узлы разбиения делят отрезок  на   отрезков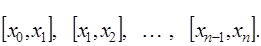

Сплайном называется составная функция 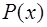, которая вместе с производными нескольких порядков непрерывна на всем отрезке 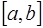, а на каждом частичном отрезке  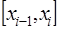в отдельности является составляющей функцией:

.

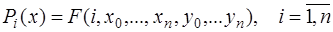Рассмотрим частный случай, когда функции 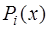 являются алгебраическими многочленами вида:

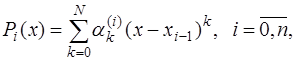
где 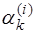 – коэффициенты, определяемые для каждого частичного отрезка.

Максимальная по всем частичным отрезкам степень многочлена называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на  производной – дефектом сплайна.

Среди существующих сплайнов наиболее широкое распространение получили сплайны следующих типов: линейные, параболические, кубические, В-сплайны.

Рассмотрим алгоритмы построения коэффициентов трех первых из перечисленных сплайнов.

 

Линейный сплайн

Сплайн 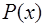 состоит из линейных многочленов вида:

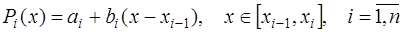.   (7.2.29)

Параметры сплайна 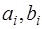,  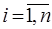определим из условия непрерывности  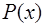на 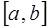 и требования совпадения значений сплайна с функцией  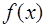в узловых точках:

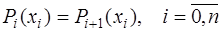,            (7.2.30)

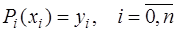.                    (7.2.31)

Обозначим 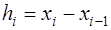. Тогда для каждого из многочленов можно записать

,        

,      

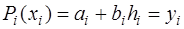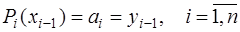и для определения коэффициентов линейного сплайна (7.2.29) получим уравнения:

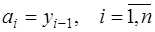,                         (7.2.32)

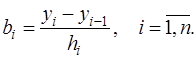                (7.2.33)

 

Параболический сплайн

Сплайн 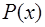 состоит из парабол, то есть  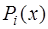имеют вид:

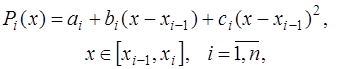   (7.2.34)

Для определения коэффициентов сплайна дополнительно к условиям (7.2.30), (7.2.31) потребуем непрерывности первой производной сплайна на интервале 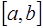, то есть:

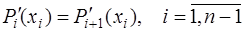.             (7.2.35)

Обозначив 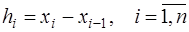, и, учитывая, что

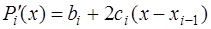,                    (7.2.36)

получим:

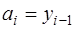,                                          (7.2.37)

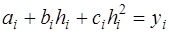,                 (7.2.38)

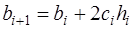.                       (7.2.39)

Тогда коэффициенты 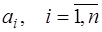 определяются согласно (7.2.37), а (7.2.38) можно записать в виде:

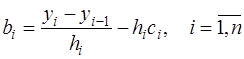.            (7.2.40)

Если теперь записать выражения для 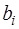 и 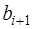 в виде (7.2.40) и подставить их в (7.2.39), то получим

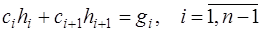,     (7.2.41)

где

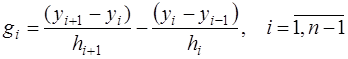. (7.2.42)

Таким образом, уравнения (7.2.37), (7.2.40) и (7.2.41) образуют систему из 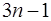 уравнений для определения  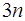коэффициентов сплайна. Недостающее уравнение получается из дополнительного условия, которое накладывается на значение производной сплайна на конце интервала 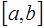, то есть:

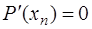                       (7.2.43)

или

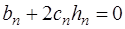.                        (7.2.44)

Если подставить в (7.2.44) выражение для 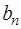 из (7.2.40), то формулу (7.2.44) можно переписать в виде:

,

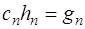где

.

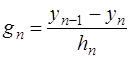Тогда

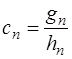                              (7.2.45)

и

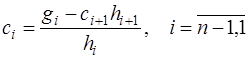.                     (7.2.46)

Таким образом, параметры параболического сплайна вычисляются в следующем порядке: сначала в обратном порядке вычисляются коэффициенты 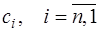 по (7.2.45), (7.2.46), затем  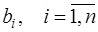по (7.2.39) и 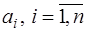, по (7.2.37).

 

Кубический сплайн

Сплайн 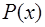 состоит из гипербол вида:

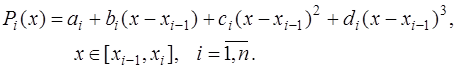(7.2.47)

Для определения параметров сплайна потребуем дополнительно к (7.2.30), (7.2.31), (7.2.35) выполнения условия непрерывности второй производной:

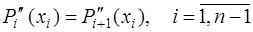.                       (7.2.48)

Первая и вторая производные отдельных многочленов сплайна соответственно равны:

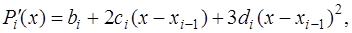       (7.2.49)

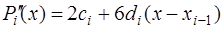.                           (7.2.50)

Тогда, обозначив 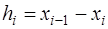, получим:

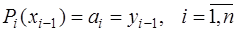,                           (7.2.51)

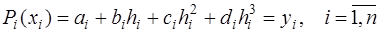, (7.2.52)

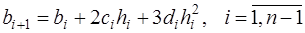,                   (7.2.53)

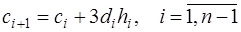.                            (7.2.54)

Последние два уравнения получены из (7.2.35) и (7.2.48).

Уравнения (7.2.51)–(7.2.54) составляют систему из 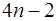 уравнений для определения  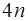параметров сплайна. Для получения двух недостающих уравнений потребуем выполнения дополнительных условий на концах интервала :

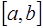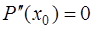,                        (7.2.55)

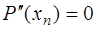.                         (7.2.56)

Тогда из (7.2.55) следует

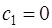,                               (7.2.57)

а из (7.2.56) получим:

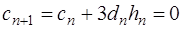.                (7.2.58)

Из уравнения (7.2.54) выразим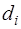

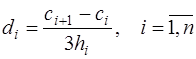,               (7.2.59)

и, подставляя его в (7.2.52), с учетом (7.2.51), получим

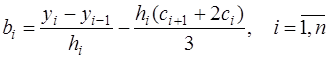. (7.2.60)

Если выражения для 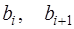 и 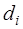 подставить в (7.2.53), то получим:

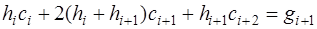,   (7.2.61)

где

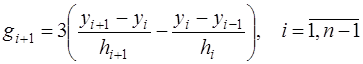.   (7.2.62)

Уравнения (7.2.61) образуют систему из 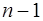 уравнения относительно неизвестных 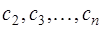. Эта система является системой с трехдиагональной матрицей вида:

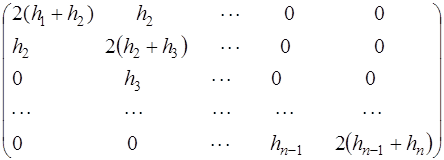(7.2.63)

и вектором свободных членов 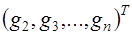, где Т - символ транспонирования.

Решение таких систем осуществляется методом прогонки, согласно которому решение представляют в виде:

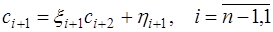,         (7.2.64)

где 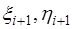 – неизвестные коэффициенты. Чтобы получить выражения для этих коэффициентов, запишем формулы для определения  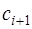и 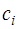 согласно (7.2.64) и, подставив их в (7.2.61), сравним полученное выражение с (7.2.64). При сравнении получим, что выражения для определения неизвестных коэффициентов  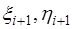будут иметь вид:

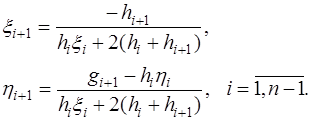       (7.2.65)

При этом, учитывая (7.2.57), полагают .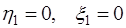

Таким образом, порядок вычисления коэффициентов кубического сплайна следующий: сначала определяют коэффициенты 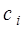, , 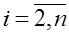для чего необходимо, осуществляя прямой ход метода прогонки по формулам (7.2.65), найти значения 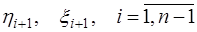, при 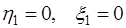, а затем, обратным ходом, считая  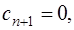по формуле (7.2.64), вычислить 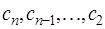. При этом, согласно (7.2.57),  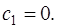Остальные коэффициенты сплайна определяются по следующим формулам:  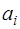– (7.2.51),  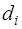   – (7.2.59),  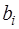– (7.2.60), .

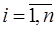Полиномиальные сплайны имеют ряд существенных недостатков:

1) при увеличении степени составных многочленов вычисление их коэффициентов значительно усложняется из-за увеличения числа уравнений (условий непрерывности функций и их производных);

2) требуется достаточно большой объем памяти для хранения информации о сплайне (точек разбиения 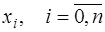 и значений коэффициентов сплайнов).

От этих недостатков в значительной мере избавлен другой вид сплайнов, который основан на базисных функциях и называется В-сплайном.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: