
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ЧАСТИНА 1. ВСТУП ДО ЛАБОРАТОРНИХ РОБІТСтр 1 из 21Следующая ⇒
ЧАСТИНА 1. ВСТУП ДО ЛАБОРАТОРНИХ РОБІТ Знаходження абсолютної похибки непрямого вимірювання методом диференціювання. Нехай для знаходження величини і Приклад 1. Об’єм циліндра:
В цьому випадку
Абсолютна похибка:
Приклад 2. Прискорення вільного падіння
тобто
Метод диференціювання зручно використовувати для знаходження абсолютної похибки непрямого вимірювання, якщо розрахункова формула має вигляд суми та різниці, тому, що диференціал суми дорівнює сумі диференціалів.
Знаходження відносної похибки непрямого вимірювання методом логарифмування з подальшим диференціюванням.
Відносною похибкою називається відношення
А так як диференціал натурального логарифма то
або Таким чином, відносна похибка результату дорівнює повному диференціалу натурального логарифму функції, яка визначає залежність даної величини від вимірюваних величин. При обрахунку потрібно брати суму абсолютних значень диференціалів всіх членів логарифма з заміною знаків ” Приклад 3. Момент інерції тіла
або Знайдемо формули абсолютної і відносної похибок результату. Для цього знайдемо спочатку відносну похибку
а) прологарифмуємо вираз для
б) візьмемо диференціал натурального логарифма і згрупуємо члени, які містять однаковий диференціал (вираз в дужках, який стоїть перед диференціалами, беруть по модулю):
в) замінивши знак ”
Абсолютна похибка
Дійсне значення моменту інерції записуємо у вигляді Визначення відносної похибки для непрямого вимірювання зручно проводити за наступними етапами: а) прологарифмувати розрахункову формулу; б) знайти від логарифма повний диференціал; в) згрупувати всі члени, які містять однаковий диференціал і вирази в дужках, які стоять перед диференціалом, взяти по модулю; г) замінити всі знаки диференціалів ” знаками абсолютних похибок вимірювань ” Приклад 4.
1. Знаходимо відносну похибку по пунктах: а) б)
в) г) 2. Розраховуємо по розрахунковій формулі (1) середній результат 3. За формулою (3) знаходимо абсолютну похибку вимірювання
4. Кінцеве значення дійсної величини буде:
Метод логарифмування з подальшим диференціюванням зручно використовувати, якщо розрахункова формула має вигляд добутків, часток та степенів. Потрібно пам’ятати, що точність результату визначається точністю вимірювальних приладів і акуратністю вихідних вимірювань і не може бути збільшена в подальшому шляхом штучного набирання знаків при виконанні арифметичних дій. Абсолютну похибку непрямого вимірювання заокруглюють до однієї значущої цифри. Відносну похибку непрямого вимірювання заокруглюють до двох значущих цифр. В наближеному числі усі цифри повинні бути вірними, за винятком останньої цифри. В подальшому будемо користуватись таким поняттям, як ”десяткові знаки” та ”значущі цифри”. Кількість десяткових знаків числа визначаються кількістю цифр, які стоять після коми, разом з нулями. . Значущими цифрами називають усі правильні цифри (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) окрім нулів на початку числа.
Наприклад:
Якщо знаходити значення похибок непотрібно, то при арифметичних діях з наближеними числами користуються наступними правилами заокруглення.
1. При додаванні та відніманні результат повинен зберігати стільки десяткових знаків, скільки їх має число з найменшою кількістю десяткових знаків та усі доданки можна заокруглювати:
2. При множенні та діленні результат повинен зберігати стільки значущих цифр, скільки їх має число з найменшою кількістю значущих цифр:
3. При піднесенні до степеня результат зберігає стільки значущих цифр, скільки їх має основа:
4. При знаходженні логарифму в результаті залишається стільки значущих цифр, скільки їх у числі, від якого брали логарифм:
ЧАСТИНА 2. МЕХАНІКА Вступ Фізичним маятником називається тверде тіло, яке під дією сили тяжіння здійснює коливний рух навколо горизонтальної осі, що не проходить через його центр інерції. При малих кутах відхилення маятник здійснює гармонічні коливання, які описуються диференціальним рівнянням: де де У формулі (3) вираз Рис. 1.1 |
У цій роботі використовується маятник (рис. 1.1), що представляє собою стержень з двома нерухомо закріпленими паралельними одна одній тригранними опорними призмами 2, на яких він може почергово підвішуватися на кронштейні 3, та сочевицями 4 і 5. Такої конструкції маятник називається оборотним. Сочевиця 4 закріплена нерухомо, а друга – 5 може переміщатися вздовж стержня. Положення сочевиці 5 на стержні визначається по шкалі 6.
ля полегшення підрахунку числа коливань маятника в роботі використовується автоматичний лічильник, що працює синхронно з електросекундоміром.
Завдання
3. Провести аналогічні виміри, підвісивши маятник на другій призмі, і результати вимірювань нанести на той же графік. Точка перетину кривих на графіку визначає таке положення сочевиці 5, якому відповідають найбільш близькі значення часу коливань маятника на кожній з призм.
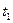 і
і 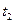 при коливаннях маятника на кожній з призм, досягаючи при цьому, щоб різниця
при коливаннях маятника на кожній з призм, досягаючи при цьому, щоб різниця 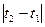 не перевищувала похибки секундоміра
не перевищувала похибки секундоміра 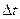 .
.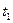 і
і 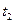 не менше трьох разів, відраховуючи кожний раз по 50 коливань. За дійсне значення часу
не менше трьох разів, відраховуючи кожний раз по 50 коливань. За дійсне значення часу 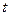 прийняти середнє з
прийняти середнє з 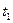 і
і 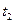 .
.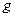 , враховуючи, що приведена довжина маятника
, враховуючи, що приведена довжина маятника  дорівнює віддалі між ребрами опорних призм, а період
дорівнює віддалі між ребрами опорних призм, а період 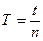 , де
, де 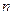 – число коливань маятника. Розрахувати похибки вимірювань.
– число коливань маятника. Розрахувати похибки вимірювань.Вступ
Вільним падінням називається рух тіла під дією тільки сили тяжіння. Якщо падіння тіла відбувається з невеликої в порівнянні з радіусом Землі висоти, то цю силу тяжіння на даній географічній широті можна вважати постійною і рівною  , де
, де  – маса тіла,
– маса тіла,  – прискорення вільного падіння. Із припущення про постійність сили тяжіння (
– прискорення вільного падіння. Із припущення про постійність сили тяжіння ( 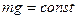 ) випливає, що при вказаних умовах
) випливає, що при вказаних умовах  , оскільки при малих швидкостях падіння тіла (у порівнянні з швидкістю світла) маса тіла постійна. Опір середовища зменшує результуюче прискорення падаючого тіла. У деяких випадках опором середовища можна знехтувати, наприклад, при падінні в повітрі сталевої кульки, і вважати падіння кульки практично вільним. У цьому випадку падіння кульки представляє собою прямолінійний рівноприскорений рух, що описується рівнянням:
, оскільки при малих швидкостях падіння тіла (у порівнянні з швидкістю світла) маса тіла постійна. Опір середовища зменшує результуюче прискорення падаючого тіла. У деяких випадках опором середовища можна знехтувати, наприклад, при падінні в повітрі сталевої кульки, і вважати падіння кульки практично вільним. У цьому випадку падіння кульки представляє собою прямолінійний рівноприскорений рух, що описується рівнянням:
 , (1)
, (1)
де  – час падіння кульки. На цьому виразі і базується метод визначення прискорення вільного падіння в даній роботі.
– час падіння кульки. На цьому виразі і базується метод визначення прискорення вільного падіння в даній роботі.
Опис установки
Установка представляє собою (рис. 1.2) вертикальну штангу 1, на якій встановлена рухома обойма 2 з прикріпленим до неї електромагнітом 3 і нерухомою ловушкою 4 з контактною заслінкою. Електромагніт служить для втримання кульки. Відлік часу падіння кульки проводиться електросекундоміром 5.
Електрична схема установки представлена на рис. 1.3 Якщо перемикачі  і
і  замкнуті, струм іде через обмотку
замкнуті, струм іде через обмотку  і кулька утримується електромагнітом. При розмиканні перемикача
і кулька утримується електромагнітом. При розмиканні перемикача  включається секундомір і виключається електромагніт, при цьому кулька відривається від електромагніту. В кінці свого падіння кулька при ударі в заслінку розмикає контакт
включається секундомір і виключається електромагніт, при цьому кулька відривається від електромагніту. В кінці свого падіння кулька при ударі в заслінку розмикає контакт  і тим самим виключає секундомір. Висоту падіння кульки можна змінювати, переміщаючи обойму 2 вздовж штанги. Відлік висоти проводиться по шкалі, що нанесена на штангу.
і тим самим виключає секундомір. Висоту падіння кульки можна змінювати, переміщаючи обойму 2 вздовж штанги. Відлік висоти проводиться по шкалі, що нанесена на штангу.
|
|
Рис. 1.2
Завдання
1. Виміряти час  падіння кульки з різних (не менше 5-ти) значень висоти
падіння кульки з різних (не менше 5-ти) значень висоти  і побудувати графік залежності
і побудувати графік залежності 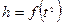 .
.
|
|
Рис. 1.3
2. З графіку визначити прискорення вільного падіння  , враховуючи, що згідно з виразом (1) графік представляє собою пряму, тангенс нахилу якої до осі абсцис рівний
, враховуючи, що згідно з виразом (1) графік представляє собою пряму, тангенс нахилу якої до осі абсцис рівний  .
.
3. Оцінити похибку визначення прискорення  .
.
Порядок виконання роботи
1. Встановити заслонку  в горизонтальне положення і включити тумблер з написом „Магніт”. Тумблер з написом „Секундомір” повинен бути при цьому виключений. Зафіксувати за допомогою електромагніту кульку.
в горизонтальне положення і включити тумблер з написом „Магніт”. Тумблер з написом „Секундомір” повинен бути при цьому виключений. Зафіксувати за допомогою електромагніту кульку.
2. Встановити стрілку секундоміра в нульове положення.
3. Включити тумблер „Секундомір”. При цьому кулька відривається від електромагніту і при ударі в заслінку  автоматично зупиняє секундомір.
автоматично зупиняє секундомір.
4. Провести вимірювання часу падіння кульки для кожного значення висоти 3-5 разів.
5. Визначити середній час для кожної висоти.
Контрольні запитання
1. Яке падіння тіл називається вільним?
2. При яких умовах прискорення вільного падіння можна вважати постійним?
3. По якому закону змінюється сила гравітаційного притягання до Землі в залежності від висоти тіла над поверхнею Землі?
Метод визначення швидкості
В даній роботі для визначення швидкості тіла використовується крутильний маятник, який представляє собою хрестовину, підвішену на пружній дротині (рис. 1.4). На горизонтальному стержні хрестовини розташовані два однакових вантажі масою  кожний, які можна переміщати вздовж стержня. На одному з кінців стержня закріплено диск
кожний, які можна переміщати вздовж стержня. На одному з кінців стержня закріплено диск  , а на другому – його противага
, а на другому – його противага  . На вертикальному стержні закріплено дзеркало 3, на яке направляється пучок світла від освітлювача. Навпроти диску
. На вертикальному стержні закріплено дзеркало 3, на яке направляється пучок світла від освітлювача. Навпроти диску  , що служить мішенню, закріплено пружний “пістолет”, призначений для надання тілу, швидкість якого треба виміряти, певного імпульсу
, що служить мішенню, закріплено пружний “пістолет”, призначений для надання тілу, швидкість якого треба виміряти, певного імпульсу  . Даний метод вимірювання швидкості тіла базується на застосуванні законів збереження моменту імпульсу і енергії до непружного співудару тіла з крутильним маятником. Тіло масою
. Даний метод вимірювання швидкості тіла базується на застосуванні законів збереження моменту імпульсу і енергії до непружного співудару тіла з крутильним маятником. Тіло масою  , випущене з „пістолета”, попадає в мішень і повертає маятник довкола вертикальної осі на невеликий кут
, випущене з „пістолета”, попадає в мішень і повертає маятник довкола вертикальної осі на невеликий кут  . Якщо удар непружний, а період коливань маятника
. Якщо удар непружний, а період коливань маятника  набагато більший від часу гальмування тіла, то, згідно з законом збереження моменту імпульсу,
набагато більший від часу гальмування тіла, то, згідно з законом збереження моменту імпульсу,
|
|
Рис. 1.4
 , (1)
, (1)
де 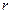 – віддаль від центру мішені до осі обертання хрестовини,
– віддаль від центру мішені до осі обертання хрестовини, 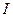 – момент інерції крутильного маятника відносно тієї ж осі,
– момент інерції крутильного маятника відносно тієї ж осі,  – початкова кутова швидкість обертання маятника після удару тіла в мішень. З другої сторони, згідно закону збереження енергії,
– початкова кутова швидкість обертання маятника після удару тіла в мішень. З другої сторони, згідно закону збереження енергії,
 , (2)
, (2)
де  – модуль кручення дротини, який залежить від пружних властивостей дротини і її розмірів. З формул (1) і (2) слідує:
– модуль кручення дротини, який залежить від пружних властивостей дротини і її розмірів. З формул (1) і (2) слідує:
 . (3)
. (3)
При повороті хрестовини довкола вертикальної осі виникає, внаслідок деформації кручення дротини, момент пружних сил, величина якого при малих кутах кручення  , згідно закону Гука, прямо пропорційна куту
, згідно закону Гука, прямо пропорційна куту  :
:
 . (4)
. (4)
Під дією цього моменту пружних сил маятник буде здійснювати крутильні коливання довкола вертикальної осі. Так як в процесі крутильних коливань маятник обертається довкола вертикальної осі, то згідно до основного закону динаміки обертового руху момент пружних сил дорівнює
 . (5)
. (5)
Прирівнюючи вирази (4) і (5), одержимо диференціальне рівняння руху крутильного маятника
 . (6)
. (6)
Розв’язок цього рівняння має вигляд
 , (7)
, (7)
де 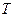 – період коливань, що дорівнює
– період коливань, що дорівнює
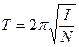 (8)
(8)
Як видно з (7), маятник буде здійснювати гармонічні коливання з кутовою амплітудою  . З врахуванням формули (8) вираз (3) для швидкості тіла приймає вид
. З врахуванням формули (8) вираз (3) для швидкості тіла приймає вид
 . (9)
. (9)
Для знаходження швидкості необхідно з виразу (9) виключити невідомий момент інерції 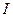 . Для цього вимірюється два періоди коливань маятника
. Для цього вимірюється два періоди коливань маятника  і
і 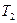 , що відповідають двом положенням вантажів на хрестовині, тобто двом моментам інерції
, що відповідають двом положенням вантажів на хрестовині, тобто двом моментам інерції  і
і 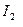 . Моменти інерції крутильного маятника
. Моменти інерції крутильного маятника  і
і  можна представити як суму моментів інерції хрестовини
можна представити як суму моментів інерції хрестовини  і моменту інерції вантажів відносно осі обертання:
і моменту інерції вантажів відносно осі обертання:

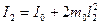 , (10)
, (10)
де  і
і 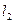 – віддалі кожного з вантажів до осі обертання відповідно при першому і другому положеннях на стержні. Тому записуючи (9) два рази отримаємо систему:
– віддалі кожного з вантажів до осі обертання відповідно при першому і другому положеннях на стержні. Тому записуючи (9) два рази отримаємо систему:
 (11)
(11)
Звідси
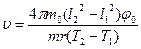 . (12)
. (12)
Завдання
1. Зафіксувати обидва вантажі  на горизонтальному стержні таким чином, щоб віддаль від центру кожного вантажу до осі обертання маятника була мінімальною і однаковою, рівною
на горизонтальному стержні таким чином, щоб віддаль від центру кожного вантажу до осі обертання маятника була мінімальною і однаковою, рівною 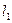 .
.
2. Встановити площину мішені перпендикулярно до горизонтальної осі „пістолета”, і направити пучок світла на нульову відмітку шкали.
3. Вистрілити з „пістолета” і за допомогою секундоміра виміряти час не менше десяти коливань маятника. По часу коливань вирахувати період  .
.
4. Визначити максимальне відхилення „зайчика” вліво і вправо від нуля по шкалі і вирахувати середнє значення  . Знайти кутову амплітуду коливань
. Знайти кутову амплітуду коливань  із співвідношення
із співвідношення  , де
, де 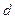 – віддаль від дзеркальця до шкали, т. я. відбитий від дзеркала промінь повертається на кут 2
– віддаль від дзеркальця до шкали, т. я. відбитий від дзеркала промінь повертається на кут 2  при повороті дзеркала разом з хрестовиною на кут
при повороті дзеркала разом з хрестовиною на кут  .
.
5. Змінити момент інерції маятника, встановивши кожний з вантажів  на віддалі
на віддалі  від осі вертикального стержня хрестовини. Визначити при цьому положенні вантажів період коливань
від осі вертикального стержня хрестовини. Визначити при цьому положенні вантажів період коливань  .
.
6. Виміряти віддаль 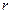 і визначити зважуванням масу тіла. Вирахувати за формулою (12) швидкість тіла. Визначити похибки.
і визначити зважуванням масу тіла. Вирахувати за формулою (12) швидкість тіла. Визначити похибки.
Вступ
Модуль зсуву є однією з характерних пружних властивостей деформованих твердих тіл. Деформація тіла, тобто зміна його форми і розмірів, відбувається під дією прикладеної до неї зовнішньої сили. Якщо після припинення дії зовнішньої сили тіло приймає початкові розміри і форму, то така деформація називається пружною, а виникаючі між різними частинами деформованого тіла внутрішні сили – пружними силами. Для кожного реального тіла існує своя границя пружності, тобто та допустима гранична величина деформації, після припинення дії якої тіло, завдяки дії пружних сил, відновлює свої розміри і форму. При деформаціях вище границі пружності зміни форми тіла стають необоротними. Така деформація називається пластичною (залишковою).
|
|
Рис. 1.5
Основними типами деформацій є деформації розтягу (стиску) і зсуву, так як деформацію любого іншого виду можна представити у вигляді суми цих двох деформацій. Зсувом називається така деформація тіла, при якій всі її плоскі шари, паралельні до площини, вздовж якої діє прикладена до тіла деформуюча сила 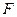 , зсунуті один відносно одного так, як показано на (рис. 1.5).
, зсунуті один відносно одного так, як показано на (рис. 1.5).
Величина деформації зсуву характеризується тангенсом кута зсуву, який називається відносним зсувом. При пружних деформаціях кут  дуже малий, тому можна прийняти, що
дуже малий, тому можна прийняти, що  . Дія деформуючої сили зрівноважується виникаючою в тілі пружною силою. Величина, що дорівнює відношенню пружної сили
. Дія деформуючої сили зрівноважується виникаючою в тілі пружною силою. Величина, що дорівнює відношенню пружної сили 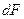 до площі поверхні
до площі поверхні  , на яку вона діє, називається напруженням. Якщо пружна сила направлена по дотичній до поверхні, то напруження називається тангенціальним і позначається
, на яку вона діє, називається напруженням. Якщо пружна сила направлена по дотичній до поверхні, то напруження називається тангенціальним і позначається  . Внаслідок взаємодії частин тіла одна з одною напруження передається у всі точки тіла так, що в любому перерізі, паралельному до площини, вздовж якої діє прикладена до тіла деформуюча сила, виникає тангенціальне напруження
. Внаслідок взаємодії частин тіла одна з одною напруження передається у всі точки тіла так, що в любому перерізі, паралельному до площини, вздовж якої діє прикладена до тіла деформуюча сила, виникає тангенціальне напруження
 . (1).
. (1).
При невеликих значеннях тангенціального напруження залежність між  і
і  можна представити законом прямої пропорційності (закон Гука):
можна представити законом прямої пропорційності (закон Гука):
 , (2)
, (2)
де  – постійний для даного матеріалу і залежний тільки від його властивостей коефіцієнт пропорційності, який називається модулем зсуву. Він дорівнює такому тангенціальному напруженню, при якому кут зсуву
– постійний для даного матеріалу і залежний тільки від його властивостей коефіцієнт пропорційності, який називається модулем зсуву. Він дорівнює такому тангенціальному напруженню, при якому кут зсуву  дорівнював би 45°
дорівнював би 45°  , якби при таких великих деформаціях не була перевищена границя пружності і зберігалась прямо пропорційна залежність між
, якби при таких великих деформаціях не була перевищена границя пружності і зберігалась прямо пропорційна залежність між  і
і  . Модуль зсуву має розмірність напруження і вимірюється в Паскалях (Па), т. я.
. Модуль зсуву має розмірність напруження і вимірюється в Паскалях (Па), т. я.  безрозмірна величина.
безрозмірна величина.
Метод вимірювання
В даній роботі метод визначення модуля зсуву оснований на вимірюваннях періоду коливань крутильного маятника, що складається з закріпленого в кронштейні зразка у вигляді циліндричного стержня, до якого закріплена горизонтальна хрестовина, навантажена чотирма однаковими вантажами (рис. 1.6). Крутильні коливання хрестовин здійснюються довкола вертикальної осі під дією моменту пружних сил, що виникає при закручуванні стержня на кут  . Цей момент при малих кутах кручення, згідно з законом Гука, пропорційний величині кута
. Цей момент при малих кутах кручення, згідно з законом Гука, пропорційний величині кута
 , (3)
, (3)
де  – коефіцієнт пропорційності, що залежить від розмірів і пружних властивостей матеріалу стержня і називається модуль кручення.
– коефіцієнт пропорційності, що залежить від розмірів і пружних властивостей матеріалу стержня і називається модуль кручення.
|
|
Рис. 1.6
При деформації кручення незакріплений переріз стержня під дією моменту зовнішніх сил повертається довкола осі стержня на кут  , внаслідок чого твірні циліндричної поверхні зсуваються на кут
, внаслідок чого твірні циліндричної поверхні зсуваються на кут  (рис. 1.7), при чому
(рис. 1.7), при чому  . Отже, в процесі закручування стержень зазнає деформації зсуву. Тому деформацію кручення можна представити як суму деформації зсуву і виразити модуль кручення стержня через модуль зсуву:
. Отже, в процесі закручування стержень зазнає деформації зсуву. Тому деформацію кручення можна представити як суму деформації зсуву і виразити модуль кручення стержня через модуль зсуву:
 , (4)
, (4)
де 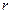 – радіус стержня,
– радіус стержня, 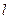 – його довжина. З цього виразу можна знайти модуль зсуву
– його довжина. З цього виразу можна знайти модуль зсуву  , якщо відомо коефіцієнт жорсткості стержня
, якщо відомо коефіцієнт жорсткості стержня  . Коефіцієнт жорсткості визначається через період коливань крутильного маятника, який, як показано в роботі №1.03, дорівнює:
. Коефіцієнт жорсткості визначається через період коливань крутильного маятника, який, як показано в роботі №1.03, дорівнює:
 , (5)
, (5)
де  – момент інерції відносно осі обертання. Для визначення модуля кручення
– момент інерції відносно осі обертання. Для визначення модуля кручення  необхідно з виразу (5) виключити момент інерції. Для цього вимірюється два періоди коливань маятника, що відповідають двом положенням вантажів на хрестовині, тобто двом моментам інерції:
необхідно з виразу (5) виключити момент інерції. Для цього вимірюється два періоди коливань маятника, що відповідають двом положенням вантажів на хрестовині, тобто двом моментам інерції:
 ;
;  ; (6)
; (6)
Моменти інерції крутильного маятника  і
і  можна представити як суму моментів інерції хрестовини разом із стержнем
можна представити як суму моментів інерції хрестовини разом із стержнем  і момент інерції вантажів відносно осі обертання
і момент інерції вантажів відносно осі обертання
 ,
,  , (7)
, (7)
де  – маса одного вантажу,
– маса одного вантажу,  і
і  – віддаль від осі обертання до центру вантажів. З виразу (6) і (7) маємо:
– віддаль від осі обертання до центру вантажів. З виразу (6) і (7) маємо:
 . (8)
. (8)
З системи двох рівнянь знайдемо модуль кручення і, відповідно до формули (4), модуль зсуву:
 , (9)
, (9)
|
Рис. 1.7 |
Завдання
1. Встановити всі чотири вантажі на віддалі 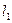 , від осі стержня. Привести маятник в коливний рух, для чого повернути хрестовину довкола вертикальної осі на невеликий кут (не більше 10°) і залишити їй свободу руху. За допомогою секундоміру виміряти час двадцяти коливань і вирахувати період коливань
, від осі стержня. Привести маятник в коливний рух, для чого повернути хрестовину довкола вертикальної осі на невеликий кут (не більше 10°) і залишити їй свободу руху. За допомогою секундоміру виміряти час двадцяти коливань і вирахувати період коливань  . Вимірювання провести не менше 5-ти разів і знайти середнє значення періоду
. Вимірювання провести не менше 5-ти разів і знайти середнє значення періоду  .
.
2. Аналогічно провести вимірювання для положення всіх чотирьох вантажів на віддалі  від осі стержня і знайти середнє значення періоду
від осі стержня і знайти середнє значення періоду  .
.
3. Виміряти довжину стержня 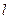 і, за допомогою мікрометра, діаметр стержня. Вимірювання цих розмірів провести декілька разів і визначити середнє значення
і, за допомогою мікрометра, діаметр стержня. Вимірювання цих розмірів провести декілька разів і визначити середнє значення  і
і 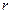 . Зважуванням знайти масу вантажу
. Зважуванням знайти масу вантажу  .
.
4. Підставивши у формулу (9) середнє значення виміряних величин, вирахувати модуль зсуву. Оцінити похибки визначення модуля зсуву.
Вступ
Момент інерції (динамічний момент інерції) є мірою інертності системи, що обертається.
Для окремої матеріальної точки, що здійснює обертовий рух, момент інерції  відносно заданої осі дорівнює добутку маси цієї точки
відносно заданої осі дорівнює добутку маси цієї точки  на квадрат віддалі
на квадрат віддалі 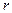 до осі обертання:
до осі обертання:
 . (1)
. (1)
Момент інерції відносно осі дорівнює сумі моментів інерції складових його частин (матеріальних точок) відносно цієї осі:
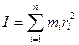 , (2)
, (2)
де 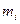 і
і  – маса матеріальної точки і її віддаль до осі обертання,
– маса матеріальної точки і її віддаль до осі обертання,  – число матеріальних точок, на яке можна розбити тіло.
– число матеріальних точок, на яке можна розбити тіло.
Як видно з (2), момент інерції тіла є величина адитивна, тобто момент інерції тіла дорівнює сумі моментів інерції його частин і момент інерції системи тіл дорівнює сумі моментів інерції окремих тіл. Одне і те ж тіло має різні моменти інерції відносно різних осей. Важливою динамічною характеристикою тіла є його момент інерції відносно осі, що проходить через центр інерції (центр мас) тіла, оскільки момент інерції тіла відносно довільної іншої осі можна представити, згідно з теоремою Штейнера, як суму моментів інерції тіла  відносно осі, що проходить через центр інерції тіла паралельно даній, і добутку маси тіла
відносно осі, що проходить через центр інерції тіла паралельно даній, і добутку маси тіла  на квадрат віддалі
на квадрат віддалі  між осями:
між осями:
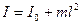 . (3)
. (3)
Момент інерції тіла залежить від його маси, конфігурації і розподілу мас в тілі відносно осі обертання. Для однорідних тіл правильної геометричної форми моменти інерції можна знайти шляхом розрахунку. Так моменти інерції циліндра (диску) і кулі відносно їх геометричних осей дорівнює

 (4)
(4)
де  і
і 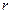 – маса і радіус вказаних тіл. Є різні методи експериментального визначення моментів інерції любих тіл. В цій роботі моменти інерції визначаються методом крутильних коливань трифілярного підвісу.
– маса і радіус вказаних тіл. Є різні методи експериментального визначення моментів інерції любих тіл. В цій роботі моменти інерції визначаються методом крутильних коливань трифілярного підвісу.
Метод вимірювань
|
|
Рис. 1.8
Трифілярний підвіс представляє собою круглу платформу, підвішену на трьох симетрично розташованих пружних нитках, які симетрично прикріплені до кільця меншого діаметра (рис. 1.8). Якщо платформу повернути на деякий кут відносно вертикальної осі, що проходить через її середину, і залишити їй свободу руху, то вона буде здійснювати крутильні коливання довкола цієї осі, причому центр інерції платформи в процесі її коливань буде переміщатися вверх і вниз по осі обертання. Суть цього методу полягає у вимірюванні періоду коливань, який визначається моментом інерції трифілярного підвісу відносно осі коливань. Співвідношення між моментом інерції трифілярного підвісу і періодом його крутильних коливань можна знайти на основі закону збереження енергії. При малих кутах повороту платформа здійснює гармонічні крутильні коливання, що описуються рівнянням:
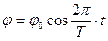 , (5)
, (5)
де  – кут повороту (кутове зміщення) платформи в момент часу
– кут повороту (кутове зміщення) платформи в момент часу  ,
,  – кутова амплітуда,
– кутова амплітуда,  – період коливань. Кутова швидкість обертання:
– період коливань. Кутова швидкість обертання:
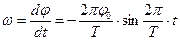 , (6)
, (6)
Як видно із формули (6) абсолютне максимальне значення кутової швидкості  , яку має платформа, переходячи через положення рівноваги, дорівнює
, яку має платформа, переходячи через положення рівноваги, дорівнює
 . (7)
. (7)
Цьому значенню кутової швидкості платформи відповідає її кінетична енергія  , рівна
, рівна
 , (8)
, (8)
де  – момент інерції платформи. У результаті повороту платформи довкола вертикальної осі на максимальний кут
– момент інерції платформи. У результаті повороту платформи довкола вертикальної осі на максимальний кут  її центр інерції переміститься по цій осі. Відносно положення рівноваги на висоту
її центр інерції переміститься по цій осі. Відносно положення рівноваги на висоту  , що відповідає приросту потенціальної енергії платформи на величину
, що відповідає приросту потенціальної енергії платформи на величину
 , (9)
, (9)
Висоту підйому платформи легко виразити через параметри трифілярного підвісу: довжини ниток підвісу  , радіус платформи
, радіус платформи  і радіус кільця
і радіус кільця 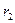 . Відповідний розрахунок, враховуючи, що кут
. Відповідний розрахунок, враховуючи, що кут 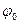 малий, дає
малий, дає
 . (10)
. (10)
За законом збереження енергії:
 . (11)
. (11)
Підставивши останній вираз у рівняння (10) знайдемо:
 (12)
(12)
По формулі (12) можна, вимірявши період коливань, визначити момент інерції як самої платформи, так і тіла, яке навантажене на платформу, оскільки, як про це сказано вище, момент інерції системи тіл дорівнює сумі моментів інерції тіл, що складають систему.
Завдання
1. Визначити момент інерції 2-3 тіл різної форми (циліндр, диск, куля) відносно їх геометричних осей. Для цього потрібно знайти момент інерції ненавантаженої платформи. Привести її в коливний рух, повернути довкола вертикальної осі на кут  і відпустити. Вимірювання часу провести не менше 5-ти разів і вирахувати середнє значення періоду коливань платформи.
і відпустити. Вимірювання часу провести не менше 5-ти разів і вирахувати середнє значення періоду коливань платформи.
2. Навантажити платформу тілом, наприклад, циліндром (диском), встановивши його таким чином, щоб центр платформи знаходився на геометричній осі (поздовжній осі симетрії) циліндра, тобто співпадав з центром основи циліндра. Визначити період коливання такої системи так само, як і період коливання ненавантаженої платформи. Таким же способом визначити період коливання системи, що складається з платформи і кулі, встановивши її на платформі симетрично до осі обертання платформи.
3. Визначити по формулі (12) момент інерції  ненавантаженої платформи. Величини
ненавантаженої платформи. Величини  ,
, 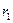 ,
,  і маса платформи даються як постійні установки. По тій же формулі визначити моменти інерції системи
і маса платформи даються як постійні установки. По тій же формулі визначити моменти інерції системи 
 , приймаючи масу системи рівною сумі мас платформи і тіла. Знайти моменти інерції тіл
, приймаючи масу системи рівною сумі мас платформи і тіла. Знайти моменти інерції тіл  як різницю
як різницю  . Визначити похибки вимірювань.
. Визначити похибки вимірювань.
4. Порівняти моменти інерції тіл з результатом розрахунків за формулою (4). Визначити точність, з якою даним методом можна визначити моменти інерції тіл.
Завдання
1. Визначити моменти інерції циліндра і кулі при різних віддалях цих тіл від осі обертання платформи, керуючись вказівками по визначенню моментів інерції, приведених у завданні 1. Для кожного з тіл вимірювання провести на 4-5 віддалях.
2. Провести не менше трьох вимірювань періоду коливань для кожної віддалі.
3. Побудувати графіки залежності виміряних моментів інерції від квадрату віддалі центру маси кожного з тіл до осі обертання. Пояснити одержані графіки.
4. Зробити висновок про точність, з якою у даному експерименті визначаються моменти інерції.
Вступ
Обертовий рух твердого тіла довкола нерухомої осі є одним з важливих видів механічного руху твердого тіла. При цьому русі усі точки тіла описують в паралельних площинах концентричні кола, центри яких знаходяться на осі, тобто обертове тіло має одну ступінь свободи, якій відповідає кут повороту. Основні кінематичні величини обертового руху: кутова швидкість  і кутове прискорення
і кутове прискорення  . Лінійні кінематичні величини окремої точки цього тіла (
. Лінійні кінематичні величини окремої точки цього тіла (  – шлях,
– шлях,  – швидкість,
– швидкість,  – тангенціальне прискорення) зв’язані з відповідними кутовими величинами, які характеризують рух усього тіла як цілого:
– тангенціальне прискорення) зв’язані з відповідними кутовими величинами, які характеризують рух усього тіла як цілого:
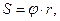

 (1)
(1)
Мірою інертності тіла, що обертається довкола нерухомої осі, є момент інерції 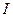 (див. роботу №1.05).
(див. роботу №1.05).
Основний закон динаміки обертового руху твердого тіла довкола нерухомої осі при постійному моменті інерції має вигляд
 , (2)
, (2)
де  – результуючий момент діючих на тіло сил відносно осі обертання,
– результуючий момент діючих на тіло сил відносно осі обертання, 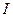 – момент інерції відносно цієї осі,
– момент інерції відносно цієї осі,  – кутове прискорення.
– кутове прискорення.
Рис. 1.9
Установка представляє собою хрестовину, яка може обертатися довкола горизонтальної осі під дією вантажу 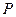 , прикріпленого до кінця шнура, намотаного на шків 2 (рис. 1.9). Чотири однакові циліндричні вантажі масою
, прикріпленого до кінця шнура, намотаного на шків 2 (рис. 1.9). Чотири однакові циліндричні вантажі масою  кожний можна переміщати вздовж стержнів і закріпляти на різних віддалях до осі обертання, змінюючи при цьому момент інерції хрестовини. Якщо підняти вантаж
кожний можна переміщати вздовж стержнів і закріпляти на різних віддалях до осі обертання, змінюючи при цьому момент інерції хрестовини. Якщо підняти вантаж 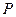 , намотуючи шнур на шків, на висоту
, намотуючи шнур на шків, на висоту  над поверхнею підлоги або стола і відпустити, то він буде падати вниз. При цьому вантаж буде рухатися з прискоренням а разом з шнуром, а хрестовина буде обертатися з кутовим прискоренням
над поверхнею підлоги або стола і відпустити, то він буде падати вниз. При цьому вантаж буде рухатися з прискоренням а разом з шнуром, а хрестовина буде обертатися з кутовим прискоренням  . Лінійна швидкість точок ободу шківа, що знаходиться на віддалі
. Лінійна швидкість точок ободу шківа, що знаходиться на віддалі  від осі обертання, дорівнює швидкості вантажу:
від осі обертання, дорівнює швидкості вантажу:
 (3)
(3)
і тангенціальне прискорення цих точок дорівнює прискоренню вантажу
 . (4)
. (4)
За другим законом Ньютона
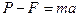 , (5)
, (5)
де 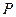 – сила тяжіння вантажу,
– сила тяжіння вантажу,  – його маса,
– його маса,  – сила натягу шнура. Звідси:
– сила натягу шнура. Звідси:
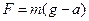 . (6)
. (6)
Сила натягу шнура  безпосередньо діє на шків, так що обертовий момент сили, що діє на хрестовину, дорівнює
безпосередньо діє на шків, так що обертовий момент сили, що діє на хрестовину, дорівнює
 , (7)
, (7)
якщо знехтувати силами тертя. Так як вантаж  рухається без початкової швидкості, то, з врахуванням (1) і (4), його прискорення
рухається без початкової швидкості, то, з врахуванням (1) і (4), його прискорення
 , (8)
, (8)
де  – час падіння вантажу,
– час падіння вантажу,  – радіус шківа,
– радіус шківа,  – кутове прискорення хрестовини. Враховуючи момент сил тертя і вважаючи його постійним, основний закон обертового руху (2) можна представити у вигляді
– кутове прискорення хрестовини. Враховуючи момент сил тертя і вважаючи його постійним, основний закон обертового руху (2) можна представити у вигляді
 , (9)
, (9)
де  – момент сили натягу шнура,
– момент сили натягу шнура,  – момент сили тертя.
– момент сили тертя.
В даній роботі безпосередньо вимірюється висота  , час падіння вантажу
, час падіння вантажу  і радіус шківа
і радіус шківа  . Знаючи ці три величини, а також масу вантажу
. Знаючи ці три величини, а також масу вантажу  , можна визначити момент інерції системи та обертовий момент сил тертя. Оцінити точність, з якою виконується основний закон динаміки обертового руху в даній роботі.
, можна визначити момент інерції системи та обертовий момент сил тертя. Оцінити точність, з якою виконується основний закон динаміки обертового руху в даній роботі.
Завдання
1. Закріпити всі рухомі вантажі на мінімальній віддалі від осі обертання, регулюючи їх положення таким чином, щоб хрестовини знаходились у рівновазі, тобто не оберталася, якщо повернути її на любий кут.
2. Намотуючи шнур на шків, підняти прикріплений до шнура вантаж  на фіксовану висоту
на фіксовану висоту  . За допомогою секундоміра визначити час падіння вантажу. Дослід повторити не менше трьох разів.
. За допомогою секундоміра визначити час падіння вантажу. Дослід повторити не менше трьох разів.
3. Провести аналогічні досліди при чотирьох віддалях рухомих вантажів  від осі обертання, проводячи кожний раз вказане у першому пункті центрування системи.
від осі обертання, проводячи кожний раз вказане у першому пункті центрування системи.
4. Вимірявши висоту  масштабною лінійкою, діаметр шківа штангенциркулем і, знаючи масу вантажу
масштабною лінійкою, діаметр шківа штангенциркулем і, знаючи масу вантажу 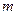 , вирахувати за формулами (8), (7) і (2) кутове прискорення і момент інерції системи для всіх чотирьох випадків розташування рухомих вантажів на стержнях. Оцінити похибки вимірювань.
, вирахувати за формулами (8), (7) і (2) кутове прискорення і момент інерції системи для всіх чотирьох випадків розташування рухомих вантажів на стержнях. Оцінити похибки вимірювань.
5. Побудувати графік залежності моменту інерції системи від кутового прискорення і пояснити одержану закономірність.
6. Побудувати графік залежності моменту інерції системи від квадрата віддалі рухомих вантажів від осі обертання.
7. Пояснити одержаний графік і знайти з цього графіка моменти інерції самої хрестовини без вантажів на стержнях.
Завдання
1. Виміряти час падіння різних по вазі вантажів (не менше п’яти), збільшуючи при кожному наступному досліді вагу закріпленого до шнура вантажу. Досліди провести при двох положеннях вантажів: на мінімальній віддалі від осі хрестовини і на кінцях стержнів, керуючись при цьому вказівками, викладеними в перших трьох пунктах завдання 1.
2. Вирахувати по формулах (8) і (7) кутове прискорення та обертовий момент сили. Оцінити похибки вимірювань.
3. Результати дослідів представити графічно, відкладаючи на осі ординат кутове прискорення і по осі абсцис – момент сили.
4. З графіків визначити момент сил тертя і моменти інерції системи.
Опис установки
Загальний вигляд установки показано на рис. 1.10. Основа 1 містить регулюючі ніжки 2, які дозволяють проводити вирівнювання приладу. В основі закріплена колонка 3, до якої прикріплено нерухомий верхній кронштейн 4 і рухомий нижній кронштейн 5. На верхньому кронштейні знаходиться електромагніт 6, фотоелектричний датчик 7 і закріплювач 8 для закріплення і регулювання довжини біфілярної підвіски маятника.
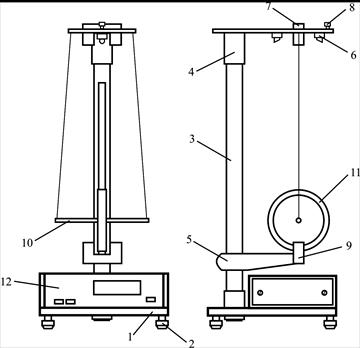
Рис. 1.10
Нижній кронштейн разом із прикріпленим до нього фотоелектричним датчиком 9 можна переміщувати вздовж колонки і фіксувати в довільно вибраному положенні.
Тіло маятника 10 є ролик, який закріплений на осі. На нього прикріпляють кільця 11, які міняють момент інерції маятника.
Маятник підтримується у верхньому положенні електромагнітом. Його довжина визначається за допомогою міліметрової шкали на колонці приладу з похибкою не більше 2 мм. Для більш точного вимірювання довжини на нижньому кронштейні наведено вказівник, який поміщений на висоті оптичної осі нижнього фотоелектричного датчика. Для вимірювання часу падіння з відносною похибкою не більше 0,02 % використовується електронна схема, яка складається з мілісекундоміра, двох фотоелектричних датчиків і електромагніту. Під час проходження маятника біля фотоелектричного датчика останній дає в схему мілісекундоміра електричний сигнал, який фіксує момент проходження маятника. Один фотоелектричний датчик з’єднаний з гніздом ZL1 мілісекундоміра 12, а інший – з гніздом ZL2.
Передня і задня панелі мілісекундоміра зображено на рис. 1.11.
На передній панелі мілісекундоміра знаходяться такі елементи:
W1 („сеть”) – вимикач живлення,
W2 („сброс”) – обнуління результатів,
W3 („пуск”) – початок вимірювання, управління магнітом.
На задній панелі мілісекундоміра знаходяться такі елементи:
ZL1, ZL2 – роз’єми для під’єднання фотоелектричних датчиків,
ZL3 – заземлення.
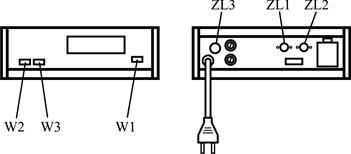
Рис. 1.11.
Порядок виконання роботи
1. Перевірити, чи співпадає нижня частина кільця маятника з нулем на колонці. Якщо не співпадає, тоді потрібно відкрутити верхній кронштейн і відрегулювати його висоту.
2. Натиснути кнопку „пуск” мілісекундоміра.
3. Встановити довжину нитки так, щоб край стального кільця після опускання маятника знаходився приблизно на 2 мм нижче оптичної осі нижнього фотоелектричного датчика. Одночасно провести регулювання установки маятника так, щоб його вісь була паралельна основі приладу.
4. Натиснути кнопку „пуск” мілісекундоміра.
5. Намотати на вісь маятника нитку підвіски.
6. Зафіксувати маятник за допомогою електромагніту.
7. Натиснути кнопку „сброс” мілісекундоміра.
8. Натиснути кнопку „пуск” мілісекундоміра.
9. Виміряти час падіння маятника в секундах за допомогою мілісекундоміра.
10. Провести аналогічні вимірювання п’ять разів.
11. Визначити висоту h в метрах, використовуючи шкалу на вертикальній колонці приладу.
12. Визначити діаметр осі разом із намотаною на неї ниткою за формулою:
 , (9)
, (9)
де Dн – діаметр нитки (Dн = 0,5 мм), діаметр Dо діаметр зовнішньої осі маятника (Dо = 10 мм).
13. Визначити масу маятника разом із кільцем за формулою:
 , (10)
, (10)
де mo – маса осі, mр – маса ролика, mк – маса кільця. Значення мас окремих елементів наведено на дослідній установці.
14. Визначити момент інерції маятника за формулою (8).
15. Визначити теоретичне значення моменту інерції за формулою:
 , (11)
, (11)
де  – момент інерції осі,
– момент інерції осі,
 – момент інерції кільця, Dк – зовнішній діаметр кільця (Dк = 105 мм), Dр – зовнішній діаметр ролика (Dр = 86 мм),
– момент інерції кільця, Dк – зовнішній діаметр кільця (Dк = 105 мм), Dр – зовнішній діаметр ролика (Dр = 86 мм),
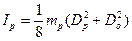 – момент інерції ролика.
– момент інерції ролика.
16. Обчислити відносну похибку визначення моменту інерції за формулою:
 , (12)
, (12)
або за формулою:

Відносна похибка не повинна перевищувати 8 %.
Контрольні запитання:
1. Сформулюйте закон збереження механічної енергії і умови його виконання.
2. Записати основний закон динаміки обертового руху.
3. Дайте визначення моменту інерції твердого тіла.
4. Запишіть формулу для визначення кінетичної енергії абсолютно твердого тіла, яке обертається навколо нерухомої осі.
5. Описати прилад і дію маятника Максвелла.
Вступ
Коливальним рухом називається рух або зміна стану, що характеризується тим чи іншим ступенем повторюваності в часі значень фізичних величин, які визначають цей рух або стан. З коливаннями ми зустрічаємось при вивченні найрізноманітніших фізичних явищ: звуку, світла, змінних струмів, радіохвиль, коливань маятників і т.д. Виявляється, що існує спільна закономірність цих явищ і математичних методів їх дослідження. Як приклад, знайдемо основне рівняння гармонічних коливань матеріальної точки (або тіла) масою 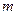 , збуджуваних пружними силами.
, збуджуваних пружними силами.
 (1)
(1)
де  – коефіцієнт пружної сили.
– коефіцієнт пружної сили.
Використаємо другий закон Ньютона:
 , (2)
, (2)
де  – прискорення частинки (тіла). Прирівнявши ці вирази, одержимо
– прискорення частинки (тіла). Прирівнявши ці вирази, одержимо
 (3)
(3)
Дане рівняння – це диференціальне рівняння вільних незагасаючих коливань, яке можна записати у вигляді:
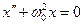 (4)
(4)
Загальний розв’язок рівняння (4) представляє собою зміну зміщення точки з положення рівноваги і має вигляд:
 , (5)
, (5)
де  – власна циклічна частота коливань точки,
– власна циклічна частота коливань точки,
 – амплітуда коливань,
– амплітуда коливань,
 – початкова фаза коливань.
– початкова фаза коливань.
У випадку фізичного маятника роль  грає кут відхилення
грає кут відхилення  , а
, а  ; для математичного маятника
; для математичного маятника  ; для електричного коливального
; для електричного коливального  -контуру роль
-контуру роль  грає заряд
грає заряд 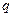 ,
,  .
.
Під дією сил тертя і опору середовища вільні коливання загасають (їх амплітуда зменшується до нульового значення). У більшості випадків величина сили опору  є пропорційна до швидкості руху частинки
є пропорційна до швидкості руху частинки
|
|
Рис. 1.13
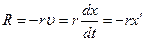 , (6)
, (6)
де  – так званий коефіцієнт сили опору.
– так званий коефіцієнт сили опору.
Диференціальне рівняння руху, в якому врахована дія сил опору, можна записати так:
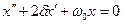 (7)
(7)
Розв’язок цього рівняння має вигляд:
 , (8)
, (8)
де  ,
,  – коефіцієнт, який пов’язаний з коефіцієнтом
– коефіцієнт, який пов’язаний з коефіцієнтом  виразом:
виразом:  ,
,  – початкова амплітуда коливань.
– початкова амплітуда коливань.
Рух точки можна розглядати як гармонічне коливання (рис. 1.13) з циклічною частотою  і амплітудою, що змінюється за законом:
і амплітудою, що змінюється за законом:
 . (9)
. (9)
Час 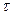 , протягом якого амплітуда зміниться в
, протягом якого амплітуда зміниться в  разів, знайдемо таким чином:
разів, знайдемо таким чином:
 , звідки
, звідки  .
.
Отже, коефіцієнт загасання обернений за величиною тому проміжку часу, за який амплітуда зменшується в 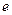 разів
разів  .
.
Період загасаючих коливань:
 (10)
(10)
При малому коефіцієнті загасання  період коливань практично дорівнює
період коливань практично дорівнює 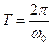 . Відношення двох сусідніх значень амплітуди коливань
. Відношення двох сусідніх значень амплітуди коливань  і
і  дорівнює:
дорівнює:
 (11)
(11)
Це відношення називається декрементом загасання, а його логарифм – логарифмічним декрементом загасання:
 . (12)
. (12)
Крім сил опору, на частинку можуть діяти інші зовнішні сили. Дуже важливу роль відіграє коливання, на яке діє сила  , величина якої міняється періодично за законом косинуса чи синуса (так звані вимушені коливання), наприклад,
, величина якої міняється періодично за законом косинуса чи синуса (так звані вимушені коливання), наприклад,
 . (13)
. (13)
Диференціальне рівняння руху, яке враховує дію зовнішньої сили  має вигляд:
має вигляд:
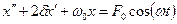 . (14)
. (14)
Розв’язком рівняння (14) є вираз:
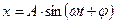 , (15)
, (15)
де  – різниця між фазою зовнішньої сили і фазою власних коливань. Величина амплітуди таких вимушених коливань рівна:
– різниця між фазою зовнішньої сили і фазою власних коливань. Величина амплітуди таких вимушених коливань рівна:
 (16)
(16)
При частоті коливань  амплітуда вимушених коливань досягає максимального значення (різко зростає). Це явище називають резонансом.
амплітуда вимушених коливань досягає максимального значення (різко зростає). Це явище називають резонансом.
Опис установки
|
Рис. 1.14 |
На основі установки (1), що на рис. 1.14, закріплена коленка (2), на якій знаходиться втулка (3) і кронштейн (4). На стержні (5), запресованому у втулці (3) кріпляться підвіски (6), на яких на підшипниках кріпиться маятник (7) і шатун (8). На стержні (7) прикріплено переривач світлового потоку (9) і прапорець (10), що служить до зміни коефіцієнта загасання коливань маятника (7). Стержні маятника (7) і шатуна (8) зв’язані між собою за допомогою пружини (11), закріпленої в спеціальній С - подібній обоймі.
Збудження коливань здійснюється за допомогою привідного диска, закріпленого на валу електродвигуна, який, рухаючи шатун (8), з’єднанній за допомогою пружини (11) з стержнем маятника (7), збуджує коливання стержня. На шатун (8) прикріплено рухомий переривач світлового потоку (12), який служить для визначення коливань шатуна. До нижнього кронштейна прикріплена кутова шкала (13), – за допомогою якої визначається амплітуда коливань маятника. В кронштейні і на корпусі установки також змонтовано фотоелектричний датчик (14), на шляху до якого світловий потік переривається переривачами світла (9) або (12).
Порядок виконання роботи
1. Визначити частоту коливань маятника. Для цього необхідно відімкнути блок живлення установки. Закріпити прапорець (10) в площині коливань маятника і відхилити стержень маятника на 8°-10° від положення рівноваги. Натиснути короткочасно кнопку ”Сброс” і коли на показчику числа коливань засвітиться цифра ”9”, натиснути кнопку "стоп"  . Знайти період коливань
. Знайти період коливань  (
(  – час десяти коливань) та циклічну частоту. Досліди повторити 5 разів.
– час десяти коливань) та циклічну частоту. Досліди повторити 5 разів.
2. Визначити коефіцієнт загасання.
Відмітити величину початкової амплітуди  і величину кінцевої амплітуди
і величину кінцевої амплітуди  за час
за час  , протягом якого відбулося
, протягом якого відбулося  коливань. В цьому випадку
коливань. В цьому випадку
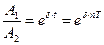 . (17)
. (17)
Розрахувати коефіцієнт загасання за допомогою формули:
 (18)
(18)
Розрахувати логарифмічний декремент загасання  (формула (12)).
(формула (12)).
Аналогічні вимірювання провести також при заданій орієнтації гальмівного прапорця і визначити коефіцієнт та логарифмічний декремент загасання.
Вступ
В рідині або в газі, у яких різні шари рухаються з неоднаковими швидкостями, виникають сили внутрішнього тертя, або так звані сили в’язкості. Дослідним шляхом встановлено, що сили внутрішнього тертя пропорційні градієнту швидкості шарів і площі поверхні дотичних шарів 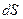 , що рухаються паралельно:
, що рухаються паралельно:
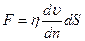 , (1)
, (1)
де  – градієнт швидкості, тобто величина, рівна зміні швидкості шарів на одиницю довжини в напрямку, перпендикулярному до напряму переміщення шарів (рис. 2.1).
– градієнт швидкості, тобто величина, рівна зміні швидкості шарів на одиницю довжини в напрямку, перпендикулярному до напряму переміщення шарів (рис. 2.1).
|
|
Рис. 2.1
Коефіцієнт пропорційності  називається динамічною в’язкістю. Чисельно він дорівнює силі внутрішнього тертя, що діє на одиницю площі шару при градієнті швидкості, рівному одиниці.
називається динамічною в’язкістю. Чисельно він дорівнює силі внутрішнього тертя, що діє на одиницю площі шару при градієнті швидкості, рівному одиниці.
Згідно молекулярно-кінетичної теорії явище внутрішнього тертя пояснюється тим, що між шарами рідини або газу відбувається обмін впорядкованого руху.
В кожному з шарів молекули рухаються з однаковою швидкістю шару і в той же час здійснюють хаотичний тепловий рух всередині шару, внаслідок якого і здійснюється їх перехід з одного шару в інший. Внаслідок хаотичності теплового руху число молекул  , що проходить за одиницю часу з шару 1 в шар 2 і навпаки (рис. 2.1) однакове, але вони переносять різні імпульси
, що проходить за одиницю часу з шару 1 в шар 2 і навпаки (рис. 2.1) однакове, але вони переносять різні імпульси  і
і  . Різниця
. Різниця  представляє собою зміну імпульсу шару
представляє собою зміну імпульсу шару 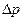 за одиницю часу. Згідно з основним рівнянням динаміки зміна імпульсу за одиницю часу рівна діючій силі
за одиницю часу. Згідно з основним рівнянням динаміки зміна імпульсу за одиницю часу рівна діючій силі  , яка і представляє собою силу внутрішнього тертя. Існують різні методи визначення динамічної в’язкості рідин. В цій роботі використовуються два методи.
, яка і представляє собою силу внутрішнього тертя. Існують різні методи визначення динамічної в’язкості рідин. В цій роботі використовуються два методи.
Метод Стокса
Цей метод основується на вимірюванні швидкості рівномірного падіння кульки в досліджуваній рідині.
На кульку радіуса  , що падає у в’язкій рідині, діє три сили:
, що падає у в’язкій рідині, діє три сили:
1. Сила тяжіння
 , (2)
, (2)
де  – густина матеріалу кульки;
– густина матеріалу кульки;
2. Виштовхувальна сила (сила Архімеда);
 , (3)
, (3)
де 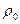 – густина рідини. Знак “мінус” означає що ця сила напрямлена в сторону, протилежну силі тяжіння
– густина рідини. Знак “мінус” означає що ця сила напрямлена в сторону, протилежну силі тяжіння  ;
;
3. Сила опору рідкого середовища, обумовлена силами внутрішнього тертя рідини. Згідно з формулою, виведеною Стоксом на основі співвідношення (1), ця сила дорівнює:
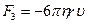 , (4)
, (4)
де 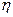 – динамічна в’язкість рідини,
– динамічна в’язкість рідини, 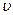 – швидкість кульки. Знак “мінус” показує, що сила опору середовища має напрямок, протилежний швидкості
– швидкість кульки. Знак “мінус” показує, що сила опору середовища має напрямок, протилежний швидкості 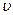 .
.
Формула (3) застосовується до твердої кульки, оточеної однорідною рідиною, якщо швидкість кульки невелика і віддаль від кульки до границі рідини значно більша, ніж її діаметр. Слід підкреслити, що у виникненні сили опору має значення не тертя кульки з рідиною, а сили тертя між шарами рідини, що захоплюються кулькою. Найближчий до поверхні кульки шар рідини рухається з швидкістю кульки. Швидкість решти шарів зменшується по мірі віддалення їх від кульки і на деякій віддалі від його поверхні дорівнює нулю.
Рівнодійна всіх сил дорівнює:
 (5)
(5)
Спочатку, поки швидкість кульки невелика, вона буде падати прискорено. Але з збільшенням швидкості кульки зростає, як видно з формули (3), сила опору 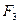 , в той час як сили
, в той час як сили  і
і  залишаються постійними. Тому через деякий час кулька досягає такої швидкості
залишаються постійними. Тому через деякий час кулька досягає такої швидкості  , при якій всі сили будуть в сумі дорівнювати нулю:
, при якій всі сили будуть в сумі дорівнювати нулю:
 (6)
(6)
тобто рух кульки буде рівномірним.
З формули(6) слідує:
 (7)
(7)
Знаючи 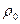 ,
,  ,
,  , визначивши швидкість рівномірного руху кульки, можна за формулою (7) знайти динамічну в’язкість.
, визначивши швидкість рівномірного руху кульки, можна за формулою (7) знайти динамічну в’язкість.
Пристрій, на якому проводять вимірювання, представляє собою циліндричну скляну посудину (рис. 2.2), наповнену досліджуваною рідиною, на якій є дві горизонтальні мітки N і M. Верхня мітка знаходиться нижче рівня рідини в тому самому місці, починаючи від якого рух кульки стає рівномірним. Діаметри кульок вимірюються мікрометром або за допомогою мікроскопа з окулярним мікрометром.
Завдання
1. Виміряти віддалі між мітками масштабною лінійкою.
2. Виміряти взаємно перпендикулярні діаметри кульки і визначити середнє з обох значень.
3. За допомогою пінцету помістити кульку над серединою поверхні рідини і, спостерігаючи за її падінням, виміряти секундоміром час, за який кулька проходить віддаль між мітками. Слід звернути увагу на те, щоб при пуску і зупинці секундоміра око було розташоване на рівні відповідної мітки.
|
|
Рис. 2.2
4. Провести вимірювання діаметра і часу падіння для кількох (не менше 5-и) кульок, виготовлених з одного матеріалу.
5. Для кожної кульки по формулі (7) визначити  – динамічну в’язкість, використовуючи табличні значення
– динамічну в’язкість, використовуючи табличні значення  і
і  .
.
6. Оцінити похибки визначення  .
.
7. Аналогічно провести вимірювання динамічної в’язкості, використовуючи інший набір кульок, що відрізняється від попереднього тільки розмірами, а також набір кульок того ж розміру, що і перший, але виготовлених з іншого матеріалу.
8. Порівняти середні значення коефіцієнта  , одержані при використанні трьох комплектів кульок, з табличним його значенням для даної температури. Проаналізувати результати експерименту.
, одержані при використанні трьох комплектів кульок, з табличним його значенням для даної температури. Проаналізувати результати експерименту.
Рис. 2.3
Прилад для визначення динамічної в’язкості даним методом називається капілярним віскозиметром і представляє собою U – подібну трубку, у вузьке коліно 1 якої впаяно капіляр 4 (рис. 2.3). При вимірюваннях рідина резервуару 3 витікає через капіляр у розширену частину трубки 5. До відростку трубки 6 приєднується ручний насос. Кільцеві мітки M і N обмежують певний постійний об’єм рідини, час витікання якого потрібно виміряти. Віскозиметр поміщають у термостат 7 таким способом, щоб розширена частина трубки 2 знаходилася нижче рівня рідини у термостаті. За допомогою виска віскозиметр повинен бути встановлений вертикально.
У термостаті міститься термометр 8.
Завдання
1. Промити віскозиметр дистильованою водою, встановити його в термостаті вертикально і закріпити. Заповнити віскозиметр дистильованою водою таким чином, щоб рівень води знаходився нижче рівня N.
2. Закрити корком отвір 9 і за допомогою ручного насоса обережно довести рівень води до половини висоти розширення 2.
3. Відкрити отвір 9 і, спостерігаючи витікання води, пустити в хід секундомір у момент проходження меніска через мітку N в момент проходження меніска через мітку М секундомір зупинити. Дослід повторити не менше 5-ти разів і визначити середнє значення 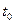 .
.
4. Аналогічно визначити час витікання досліджуваної рідини, попередньо промивши віскозиметр невеликою кількістю даної рідини. Знайти середнє значення часу  .
.
5. За формулою (10) визначити коефіцієнт  , використовуючи табличні значення
, використовуючи табличні значення  ,
,  і
і 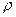 . При цьому необхідно взяти табличні значення
. При цьому необхідно взяти табличні значення  , що відповідають температурі води у термостаті під час досліду.
, що відповідають температурі води у термостаті під час досліду.
6. Оцінити похибки вимірювань.
Контрольні запитання:
1. Який фізичний зміст динамічної в’язкості?
2. Як пояснити з погляду молекулярно-кінетичної теорії виникнення сили в’язкості?
3. У чому полягає метод Стокса?
4. Яка методика визначення динамічної в’язкості на основі методу Пуазейля?
Рис. 2.4
Установка (рис. 2.4) складається з наповненого водою аспіратора 1, капіляра 2 і манометра 3. При витіканні води через кран 4 тиск в аспіраторі знижується і через капіляр в аспіратор всмоктується сухе повітря, яке попередньо проходить через осушувач 5. Різницю тисків  , що виникає на кінцях капілярної трубки, вимірюється за допомогою манометра
, що виникає на кінцях капілярної трубки, вимірюється за допомогою манометра
 , (8)
, (8)
де  – густина рідини в манометрі, різниця висот рівнів
– густина рідини в манометрі, різниця висот рівнів  в манометрі,
в манометрі, 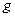 – прискорення вільного падіння. Об’єм повітря, яке протікає через капіляр, визначається по об’єму води, що витікає з аспіратора.
– прискорення вільного падіння. Об’єм повітря, яке протікає через капіляр, визначається по об’єму води, що витікає з аспіратора.
Завдання
1. Обережно відкрити кран 4, визначити час  витікання 300 мл води. Визначити за допомогою манометра різницю тисків
витікання 300 мл води. Визначити за допомогою манометра різницю тисків  . Дослід повторити 5-7 разів. Знайти середнє значення
. Дослід повторити 5-7 разів. Знайти середнє значення  і
і  .
.
2. Використовуючи формулу (7), визначити динамічну в’язкість  . Радіус капіляра і його довжина дані як постійні приладу.
. Радіус капіляра і його довжина дані як постійні приладу.
3. За формулою (3) визначити швидкість молекул газу.
4. За формулою (4) знайти густину газу. При цьому тиск повітря 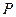 , його температура
, його температура  визначається за показами термометра і барометра, які є в приміщенні лабораторії.
визначається за показами термометра і барометра, які є в приміщенні лабораторії.
5. Використовуючи формули (5) і (6), визначити ефективний діаметр молекул повітря.
6. Знайти похибки визначення  і
і 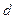 .
.
Контрольні запитання
1. В чому суть методу визначення середньої довжини вільного пробігу молекул в цій роботі?
2. Яка методика визначення динамічної в’язкості повітря в даній роботі?
3. Чому діаметр молекул називається ефективним?
Рис. 2.5
Установка (рис. 2.5) представляє собою посудину 1, заповнену повітрям і під’єднану до водяного манометра 2 і ручного насосу 3. За допомогою крану 4 посудина може з’єднуватись з атмосферою. Нехай спочатку повітря в посудині об’ємом 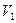 , знаходиться під тиском
, знаходиться під тиском 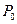 . Якщо за допомогою насосу нагнітати в посудину деяку кількість повітря, то тиск і температура повітря всередині посудини підвищаться. Через деякий час (при закритих кранах 4 і 5) внаслідок теплообміну з оточуючим середовищем температура повітря в посудині зрівняється з температурою зовнішнього середовища
. Якщо за допомогою насосу нагнітати в посудину деяку кількість повітря, то тиск і температура повітря всередині посудини підвищаться. Через деякий час (при закритих кранах 4 і 5) внаслідок теплообміну з оточуючим середовищем температура повітря в посудині зрівняється з температурою зовнішнього середовища 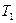 , а тиск, що встановиться в посудині, дорівнює
, а тиск, що встановиться в посудині, дорівнює  , де
, де 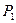 – додатковий тиск, вимірюваний різницею висот рівнів рідини в манометрі. Цей перший стан повітря в посудині характеризується параметрами
– додатковий тиск, вимірюваний різницею висот рівнів рідини в манометрі. Цей перший стан повітря в посудині характеризується параметрами 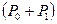 ,
, 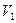 ,
, 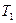 . Якщо тепер відкрити на короткий час кран 4, то повітря в посудині буде розширюватися адіабатно, оскільки за короткий проміжок часу не встигне здійснитися теплообмін між повітрям в посудині і зовнішнім середовищем. В кінці адіабатного розширення повітря в посудині встановлюється атмосферний тиск, температура знижується до
. Якщо тепер відкрити на короткий час кран 4, то повітря в посудині буде розширюватися адіабатно, оскільки за короткий проміжок часу не встигне здійснитися теплообмін між повітрям в посудині і зовнішнім середовищем. В кінці адіабатного розширення повітря в посудині встановлюється атмосферний тиск, температура знижується до 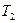 , а об’єм залишається рівним
, а об’єм залишається рівним 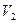 . Це буде другий стан повітря (параметри
. Це буде другий стан повітря (параметри 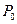 ,
, 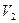 ,
, 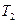 ). Якщо зразу в кінці адіабатного процесу, коли тиск в посудині впаде до атмосферного, закрити кран 4, то охолоджене повітря в посудині буде нагріватися і його тиск почне зростати. Тиск зросте до величини
). Якщо зразу в кінці адіабатного процесу, коли тиск в посудині впаде до атмосферного, закрити кран 4, то охолоджене повітря в посудині буде нагріватися і його тиск почне зростати. Тиск зросте до величини 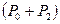 , коли повітря в посудині нагріється до температури зовнішнього середовища
, коли повітря в посудині нагріється до температури зовнішнього середовища 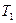 . Таким чином, третій стан газу характеризується параметрами
. Таким чином, третій стан газу характеризується параметрами 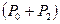 ,
, 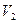 і
і 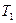 .
.
Адіабатний перехід з першого стану до другого описується рівнянням (4):
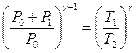 (5)
(5)
Перехід від другого стану до третього проходить без зміни об’єму (ізохорний процес). Застосувавши до цього переходу рівняння, що описує ізохорний процес, одержимо:
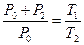 . (6)
. (6)
Розв’язуючи сумісно рівняння (5) і (6), знайдемо:
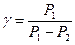 (7)
(7)
Так як тиски 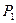 і
і 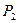 , вимірювані манометром, пропорційні відповідним різницям висот в манометрі
, вимірювані манометром, пропорційні відповідним різницям висот в манометрі 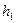 і
і 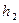 , то остаточно
, то остаточно
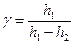 . (8)
. (8)
Завдання
1. За допомогою насоса обережно нагнітати в посудину деяку кількість повітря, щоб різниця рівнів рідини в манометрі дорівнювала приблизно 200 мм. Через 2-3 хвилини газ в посудині набуває кімнатної температури. Зробити відлік по шкалі різниці рівнів 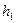 .
.
2. Швидко відкрити кран 4 і, після вирівнювання рівнів рідини в манометрі, закрити кран. Через 2-3 хвилини зробити другий відлік різниці рівнів  .
.
3. Дослід повторити 7-10 разів.
4. Вирахувати за формулою (8) для кожного окремого досліду показник адіабати 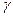 . Знайти його середнє значення і оцінити похибки.
. Знайти його середнє значення і оцінити похибки.
5. Порівняти одержане значення 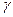 з його теоретичним значенням, визначеним за формулою (2), і пояснити причини розходження між цими значеннями.
з його теоретичним значенням, визначеним за формулою (2), і пояснити причини розходження між цими значеннями.
Вступ
Поверхневий натяг  вимірюється роботою
вимірюється роботою  ізотермічного утворення одиниці площі
ізотермічного утворення одиниці площі  поверхні рідини на границі з другою фазою:
поверхні рідини на границі з другою фазою:
 (1)
(1)
Якщо поверхня рідини обмежена лінією (периметром змочування) довжиною  , то поверхневий натяг дорівнює силі, що діє на одиницю довжини периметра і напрямленій перпендикулярно до неї
, то поверхневий натяг дорівнює силі, що діє на одиницю довжини периметра і напрямленій перпендикулярно до неї  . Ця сила лежить в площині, дотичній до вільної поверхні рідини.
. Ця сила лежить в площині, дотичній до вільної поверхні рідини.
На молекули рідини, що знаходяться в поверхневому шарі, діють напрямлені всередину рідини не скомпенсовані сили притягання з сторони інших молекул всередині рідини. В результаті цього молекули поверхневого шару мають більшу потенціальну енергію, ніж молекули, що знаходяться всередині рідини, оскільки при ізотермічному переході молекул з об’єму рідини на її поверхню здійснюється робота по подоланню напрямлених всередину рідини сил, що діє на поверхневий шар. Ця робота збільшує потенціальну енергію молекул, що переходять на поверхню. Стану стійкої рівноваги рідини відповідає мінімум потенціальної енергії її вільної поверхні, що рівнозначне найменшій площі цієї поверхні. Тому рідина намагається скоротити площу вільної поверхні, внаслідок чого в поверхневому шарі виникають сили натягу, напрямлені вздовж поверхні. Ці сили подібні до пружних сил, які намагаються скоротити площу поверхні механічно розтягнутої плівки.
Метод вимірювання
Суть методу полягає у вимірюванні в капілярі тиску рідини  , обумовленого силами поверхневого натягу рідини, шляхом його компенсації додатковим тиском стискуваного повітря.
, обумовленого силами поверхневого натягу рідини, шляхом його компенсації додатковим тиском стискуваного повітря.
Установка складається з капіляра 1, яким торкаються поверхні досліджуваної рідини в посудині, манометра 3, з’єднаного з капіляром, і трубкою 2 (рис. 2.6). Обидві посудини знаходяться на столиках 5 і 6, висоту яких можна плавно змінювати.
Як відомо, при повному змочуванні рідиною стінок капіляру з циліндричним каналом додатковий тиск її вгнутої поверхні, що називається меніском, визначається формулою
 , (3)
, (3)
де  – радіус капілярної трубки. Цей тиск, напрямлений вгору до центру кривизни сферичної поверхні меніска, піднімає рідину в капілярі до такого рівня по відношенню до поверхні рідини в широкій посудині, щоб тиск стовпа піднятої рідини зрівноважував додатковий тиск
– радіус капілярної трубки. Цей тиск, напрямлений вгору до центру кривизни сферичної поверхні меніска, піднімає рідину в капілярі до такого рівня по відношенню до поверхні рідини в широкій посудині, щоб тиск стовпа піднятої рідини зрівноважував додатковий тиск  . Якщо піднімати столик 6, то тиск повітря у всій системі (капіляр-трубка 2 - манометр) буде зростати внаслідок зменшення об’єму системи і рідина в капілярі почне опускатися. Очевидно, що при досягненні певного значення тиску повітря меніск в капілярі виявиться на рівні досліджуваної рідини в широкій посудині, тобто тиск повітря в системі, що вимірюється манометром, буде становити
. Якщо піднімати столик 6, то тиск повітря у всій системі (капіляр-трубка 2 - манометр) буде зростати внаслідок зменшення об’єму системи і рідина в капілярі почне опускатися. Очевидно, що при досягненні певного значення тиску повітря меніск в капілярі виявиться на рівні досліджуваної рідини в широкій посудині, тобто тиск повітря в системі, що вимірюється манометром, буде становити  . Знаючи радіус капіляра
. Знаючи радіус капіляра  , можна за формулою (3) знайти
, можна за формулою (3) знайти  .
.
|
|
Рис. 2.6
Завдання
1. Промити капілярну трубку спиртом, а потім досліджуваною рідиною і, піднімаючи столик 5, торкнутися капіляром до поверхні досліджуваної рідини.
2. Опустити столик 6 таким чином, щоб рівень рідини в посудині, розташованій на цьому столику, знаходився нижче зрізу трубки 2. При цьому в системі встановлюється атмосферний тиск.
3. Встановити рівень рідини в манометрі на нульову відмітку.
4. Піднімаючи столик 6, сумістити меніск в капілярі з рівнем досліджуваної рідини в посудині.
5. Зробити відлік положення рідини по шкалі похилої трубки 7 мікроманометра. Трубка мікроманометра встановлюється під кутом  до горизонтальної поверхні для збільшення точності вимірювання тиску. Тиск, вимірюваний мікроманометром, дорівнює:
до горизонтальної поверхні для збільшення точності вимірювання тиску. Тиск, вимірюваний мікроманометром, дорівнює:
 , (4)
, (4)
де  – відлік по шкалі манометра,
– відлік по шкалі манометра,  – густина рідини, яка знаходиться в манометрі,
– густина рідини, яка знаходиться в манометрі,  – прискорення вільного падіння.
– прискорення вільного падіння.
6. Вирахувати поверхневий натяг рідини σ за формулою:
 , (5)
, (5)
яку отримали з врахуванням (3) і (4).
7. Радіус r капіляру дається як постійна приладу.
8. Повторити дослід не менше 5-ти разів і визначити середнє значення  .
.
9. Оцінити похибку визначення  .
.
Контрольні запитання:
1. Який фізичний зміст поверхневого натягу  ?
?
2. Як пояснити існування сил поверхневого натягу?
3. Яка методика визначення додаткового тиску в капілярі?
Метод вимірювання
Поверхневий натяг  , фізичний зміст якого розглянуто в роботі №2.04, залежить від хімічного складу рідини і її температури. Із збільшенням температури
, фізичний зміст якого розглянуто в роботі №2.04, залежить від хімічного складу рідини і її температури. Із збільшенням температури  зменшується і досягає нуля при критичній температурі.
зменшується і досягає нуля при критичній температурі.
|
|
Рис. 2.6
Суть даного методу визначення  полягає у вимірюванні тиску в бульбашці повітря, що протискується з вузького каналу трубки в досліджувану рідину. Прилад (рис. 2.6) складається з щільно закритої посудини 1, в яку налито деяку кількість досліджуваної рідини, манометра 2 і наповненого водою аспіратора 3. Повітряний простір посудини 1 з’єднаний гумовими трубками через розподільник 4 з манометром і аспіратором. В посудині 1 встановлено трубку 5 з вузьким вихідним каналом на кінці таким чином, щоб цей кінець знаходився дещо нижче від поверхні рідини (на 0,5 мм). За допомогою крану 6 всю систему можна з’єднати з атмосферою. Посудину 1 поміщають в термостат 7. Якщо легко відкрити кран 8, попередньо закривши кран 6, то з аспіратора почне повільно витікати вода, а у верхній частині аспіратора і у з’єднаній з ним посудині 1 та у правому коліні манометра тиск повітря почне зменшуватися. При досягненні певного степеня розрідження повітря надлишок атмосферного тиску проштовхує через вихідний канал трубки 5 бульбашку повітря. Це відбувається тоді, коли різниця тисків атмосферного повітря у відкритій трубці 5 і повітря в посудині 1, яка вимірюється різницею рівнів рідини в манометрі, зрівноважує тиск, викликаний силами поверхневого натягу рідини, що оточує утворювану бульбашку, внаслідок кривизни її шару на границі з бульбашкою. Тиск обумовлений кривизною поверхні рідини, пропорційний, як відомо, поверхневому натягу
полягає у вимірюванні тиску в бульбашці повітря, що протискується з вузького каналу трубки в досліджувану рідину. Прилад (рис. 2.6) складається з щільно закритої посудини 1, в яку налито деяку кількість досліджуваної рідини, манометра 2 і наповненого водою аспіратора 3. Повітряний простір посудини 1 з’єднаний гумовими трубками через розподільник 4 з манометром і аспіратором. В посудині 1 встановлено трубку 5 з вузьким вихідним каналом на кінці таким чином, щоб цей кінець знаходився дещо нижче від поверхні рідини (на 0,5 мм). За допомогою крану 6 всю систему можна з’єднати з атмосферою. Посудину 1 поміщають в термостат 7. Якщо легко відкрити кран 8, попередньо закривши кран 6, то з аспіратора почне повільно витікати вода, а у верхній частині аспіратора і у з’єднаній з ним посудині 1 та у правому коліні манометра тиск повітря почне зменшуватися. При досягненні певного степеня розрідження повітря надлишок атмосферного тиску проштовхує через вихідний канал трубки 5 бульбашку повітря. Це відбувається тоді, коли різниця тисків атмосферного повітря у відкритій трубці 5 і повітря в посудині 1, яка вимірюється різницею рівнів рідини в манометрі, зрівноважує тиск, викликаний силами поверхневого натягу рідини, що оточує утворювану бульбашку, внаслідок кривизни її шару на границі з бульбашкою. Тиск обумовлений кривизною поверхні рідини, пропорційний, як відомо, поверхневому натягу  . Значить, в момент відриву бульбашки виконується співвідношення:
. Значить, в момент відриву бульбашки виконується співвідношення:
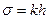 , (1)
, (1)
де  – різниця тисків, що вимірюється манометром,
– різниця тисків, що вимірюється манометром,  – коефіцієнт пропорційності, який залежить від розмірів вихідного отвору трубки і є постійною величиною даного приладу. Для визначення
– коефіцієнт пропорційності, який залежить від розмірів вихідного отвору трубки і є постійною величиною даного приладу. Для визначення 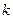 необхідно провести дослід з рідиною, поверхневий натяг
необхідно провести дослід з рідиною, поверхневий натяг  якої відомий, наприклад, з водою. Тоді, підставивши відповідне значення
якої відомий, наприклад, з водою. Тоді, підставивши відповідне значення  і
і 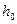 в формулу (1), одержимо остаточне значення для визначення поверхневого натягу:
в формулу (1), одержимо остаточне значення для визначення поверхневого натягу:
 . (2)
. (2)
Завдання
1. Залити в аспіратор воду, а посудину 1 заповнити дистильованою водою до такого рівня, щоб кінець трубки 5 знаходився від поверхні води на віддалі не більше 0,5 мм.
2. Відкривши кран 6 встановити в системі атмосферний тиск. Рівні рідин в колінах манометра при цьому вирівнюються.
3. Закрити кран 6, відкрити кран аспіратора настільки, щоб зміна тиску відбувалась достатньо повільно і можна було відрахувати висоти рівнів в манометрі в момент відриву бульбашки.
4. Після встановлення певної частоти утворення бульбашок почати відлік по манометру, відмічаючи різницю рівнів в момент відриву кожної бульбашки. Провести не менше 10 відліків і знайти середнє значення різниці рівнів. Виміряти температуру термостата.
5. Розрахувати за формулою (1) коефіцієнт пропорційності – постійну приладу  .
.
6. Аналогічно визначити поверхневий натяг для досліджуваного розчину при різних температурах. Побудувати графік залежності  . Визначити
. Визначити  для різних концентрацій даного розчину при постійній температурі і побудувати графік залежності
для різних концентрацій даного розчину при постійній температурі і побудувати графік залежності  від концентрації.
від концентрації.
Контрольні запитання
1. Яка температура називається критичною?
2. Яка формула тиску викривленої поверхні рідини?
3. Яка методика визначення поверхневого натягу в даній роботі?
Вступ
Ентропія є функція стану макросистеми, що характеризує напрямок протікання самовільних процесів в ізольованій термодинамічній системі. Якщо система переходить  з одного стану в інший, то зміна ентропії в результаті такого процесу не залежить від виду процесу, а визначається різницею ентропії системи в кінцевому і початковому станах. Зміна ентропії в системі при нескінченно малій зміні її стану дорівнює:
з одного стану в інший, то зміна ентропії в результаті такого процесу не залежить від виду процесу, а визначається різницею ентропії системи в кінцевому і початковому станах. Зміна ентропії в системі при нескінченно малій зміні її стану дорівнює:
 , (1)
, (1)
де  – ентропія,
– ентропія,  – термодинамічна температура системи,
– термодинамічна температура системи,  – кількість теплоти, що надається системі. При кінцевому оборотному переході системи з стану 1 в стан 2 зміна ентропії дорівнює:
– кількість теплоти, що надається системі. При кінцевому оборотному переході системи з стану 1 в стан 2 зміна ентропії дорівнює:
 . (2)
. (2)
У випадку ізотермічного процесу  . Наприклад, зміна ентропії при випаровуванні рідини дорівнює скритій теплоті випаровування, поділеній на температуру випаровування. Для довільного кругового оборотного процесу
. Наприклад, зміна ентропії при випаровуванні рідини дорівнює скритій теплоті випаровування, поділеній на температуру випаровування. Для довільного кругового оборотного процесу  . Всі реальні процеси в ізольованих системах відбуваються таким чином, що ентропія системи зростає. В цьому твердженні міститься зміст другого закону термодинаміки.
. Всі реальні процеси в ізольованих системах відбуваються таким чином, що ентропія системи зростає. В цьому твердженні міститься зміст другого закону термодинаміки.
Метод вимірювання
В даній роботі визначають зміну ентропії  при нагріванні і охолодженні олова масою
при нагріванні і охолодженні олова масою  . Кількість теплоти, необхідна для нагрівання олова від початкової температури
. Кількість теплоти, необхідна для нагрівання олова від початкової температури  до температури плавлення
до температури плавлення  визначається, як відомо, по формулі
визначається, як відомо, по формулі
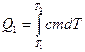 , (2)
, (2)
де  – питома теплоємність олова. Кількість теплоти
– питома теплоємність олова. Кількість теплоти  , затрачена на плавлення олова при постійній температурі
, затрачена на плавлення олова при постійній температурі  , дорівнює:
, дорівнює:
 , (3)
, (3)
де  – питома теплота плавлення олова. Зміна ентропії при нагріванні олова визначається за формулою:
– питома теплота плавлення олова. Зміна ентропії при нагріванні олова визначається за формулою:
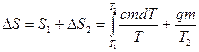 (4)
(4)
Після інтегрування одержимо:
 (5)
(5)
|
|
Рис. 2.7
Установка (рис. 2.7) складається з тигельної печі (1), термопари (2), мілівольтметра, включеного в коло термопари і тигля з оловом (3), розміщеного в печі. Один з кінців термопари розміщено в тигель з оловом (3), другий знаходиться в посудині з маслом (4) при кімнатній температурі. Температура плавлення олова визначається за показами мілівольтметра.
Завдання
1. Визначити зважуванням масу олова, розмістити тигель з оловом у піч і встановити термопару.
2. Включити піч, нагріти і розплавити олово. Визначити температуру плавлення олова та поміряти температуру масла.
3. По формулі (5) визначити приріст ентропії. Визначити похибки.
Контрольні запитання:
1. Який фізичний зміст ентропії ?
2. В чому полягає зміст другого закону термодинаміки ?
3. Які термодинамічні процеси називаються оборотними ?
Рис. 2.8
Прирівнюючи швидкості охолодження двох нагрітих зразків (швидкості зниження їх температур), можна визначити теплоємність одного з них, якщо відома теплоємність другого. Кількість теплоти  , яку віддає металевий зразок масою
, яку віддає металевий зразок масою  при зниженні його температури на
при зниженні його температури на  , визначається як відомо, за формулою:
, визначається як відомо, за формулою:
 , (1)
, (1)
де  – питома теплоємність металу. Ця ж кількість теплоти переноситься через площадку поверхні зразка в оточуюче середовище і ії можна визначити за законом теплопровідності Фур’є
– питома теплоємність металу. Ця ж кількість теплоти переноситься через площадку поверхні зразка в оточуюче середовище і ії можна визначити за законом теплопровідності Фур’є
 , (2)
, (2)
де  – коефіцієнт теплопровідності,
– коефіцієнт теплопровідності, 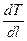 – градієнт температури, тобто зміна температури на одиницю довжини в напрямку нормалі до поверхні зразка. Таким чином
– градієнт температури, тобто зміна температури на одиницю довжини в напрямку нормалі до поверхні зразка. Таким чином
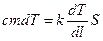 (3)
(3)
Записавши це співвідношення для двох зразків з врахуванням того, що для однакових по розмірах і формі зразків  ,
,  однакові, то
однакові, то
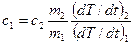 . (4)
. (4)
Установка (рис. 2.8) складається з електропечі 1 з боковим отвором, в який вставляють зразки 2, виготовлені у вигляді однакових циліндрів. В кожному із зразків є канал, у який вставляють термопару, підключену до гальванометра 3, шкала якого проградуйована в градусах Цельсія.
Завдання
1. Нагріти мідний (еталонний) зразок до температури 600°С і виключити електропіч.
2. В процесі охолодження зразка через кожні 10-15 секунд проводять відлік температури по показах гальванометра. Після охолодження зразка до температури нижче 100°С дослід повторюють ще раз. Аналогічні досліди провести для досліджуваного зразка.
3. Для кожного зразка побудувати графіки залежності температури від часу по середніх значеннях температур.
4. Одержані криві  перевести в криві
перевести в криві  графічним методом.
графічним методом.
5. Користуючись графіками 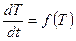 і формулою (4) визначити питому теплоємність досліджуваних зразків при різних значеннях температури. При цьому з таблиці, приведеної нижче, взяти значення теплоємності міді о області температур від 373 до 673 К
і формулою (4) визначити питому теплоємність досліджуваних зразків при різних значеннях температури. При цьому з таблиці, приведеної нижче, взяти значення теплоємності міді о області температур від 373 до 673 К
| Т, К | 373 | 473 | 573 | 673 | 773 | 873 |
| С, Дж/кг∙К | 394 | 408 | 422 | 434 | 448 | 456 |
6. Побудувати графіки залежності питомої теплоємності від температури для всіх досліджуваних зразків.
Додаткові вказівки
1. Для побудови графіка  провести на графіку
провести на графіку 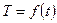 ряд вертикальних ліній через рівні проміжки
ряд вертикальних ліній через рівні проміжки 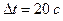 . З різниці значень ординат кривої в точках перетину її вертикальними прямими знайти різниці температур для відповідних інтервалів часу. Відношення цієї різниці температур до інтервалу часу дасть швидкість охолодження металу в даній точці кривої, тобто швидкість охолодження зразка при певній температурі.
. З різниці значень ординат кривої в точках перетину її вертикальними прямими знайти різниці температур для відповідних інтервалів часу. Відношення цієї різниці температур до інтервалу часу дасть швидкість охолодження металу в даній точці кривої, тобто швидкість охолодження зразка при певній температурі.
2. На основі цих даних побудувати таблицю значень 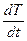 і
і  та побудувати графіки залежності
та побудувати графіки залежності  для всіх зразків.
для всіх зразків.
Контрольні запитання
1. В чому полягає суть методу визначення теплоємності в даній роботі ?
2. Який метод побудови кривих залежності швидкості охолодження зразка від температури ?
Вступ
Теплове розширення твердих тіл, причиною якого є збільшення амплітуди теплових коливань атомів при нагріванні твердих тіл, характеризується температурним коефіцієнтом лінійного розширення  , який дорівнює відносному видовженню
, який дорівнює відносному видовженню  тіла при його нагріванні на один Кельвін:
тіла при його нагріванні на один Кельвін:
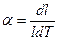 (1)
(1)
де  – зміна довжини
– зміна довжини  тіла при зміні його температури на величину
тіла при зміні його температури на величину  . Для більшості твердих тіл при невеликих змінах температури
. Для більшості твердих тіл при невеликих змінах температури  незначно залежить від температури. Тому в невеликому інтервалі температур (
незначно залежить від температури. Тому в невеликому інтервалі температур (  ) можна використати середнє значення
) можна використати середнє значення  :
:
 (2)
(2)
де  – інтервал температур, якому відповідають довжини тіла
– інтервал температур, якому відповідають довжини тіла  і
і  . В даній роботі застосовується метод прямого (безпосереднього) вимірювання видовження за допомогою оптиметра – приладу високого класу точності.
. В даній роботі застосовується метод прямого (безпосереднього) вимірювання видовження за допомогою оптиметра – приладу високого класу точності.
Опис установки
|
|
Рис. 2.9
|
Рис. 2.10 |
Установка (рис. 2.9) складається з оптиметра 1, нагрівника 2, в який поміщено зразок (стержень) 3 і термостат 4, що служить для нагрівання води до певної температури. Вода поступає по з’єднуючих шлангах в нагрівник, в результаті чого стержень нагрівається до цієї температури і видовжується.
Оптиметр складається з масивної основи 5 і вертикальної колонки 6, вздовж якої може переміщатись трубка 7 з оптичним мікроскопом 9. В нижній частині трубки знаходиться виступаючий наконечник вимірювального штифта 8, що дотикається до поверхні зразка. На вимірювальному штифті, що розміщується всередині трубки, закріплена шкала, що переміщається разом зі штифтом в полі зору мікроскопу 9 при видовженні зразка. Відлік визначається (див. рис. 2.10) положенням нуля прямолінійної шкали, розділеної на 10 поділок (ціна поділки 0,1 мм), відносно зображення основної міліметрової шкали (на рис. 2.10 між поділками 53 і 54 мм). Щоб визначити віддаль нуля від штриха 53 мм, обертають гвинт 10 так, щоб найближчий подвійний виток співпадав з цим штрихом, тобто штрих 53 знаходився посередині між лініями найближчого подвійного витка. Десяті долі відраховуються по прямолінійній шкалі. Соті і тисячні – по круговій, видимій у верхній частині поля зору окуляра. Наприклад, на рис. 2.10 відлік дорівнює 53,1374 мм.
Завдання
1. Визначити штангенциркулем довжину зразка і помістити його в нагрівник. Відрегулювати положення нагрівника за допомогою гвинтів так, щоб зразок був розташований вертикально вздовж осі вимірювання. Звільнивши затискуючий гвинт трубки 7, перемістити його вниз до дотику наконечника 8 з торцем зразка. Звільнити фіксатор вимірювальної системи. Включити освітлювач відлікового пристрою, відрегулювати різкість зображення, обертаючи окуляр.
2. Включити термостат і встановити потрібну температуру (інструкція по експлуатації термостата додається). Почекати 3-5 хв до встановлення стабільної температури, провести відлік по шкалі оптиметра. Продовжити нагрівання зразка, провести аналогічні відліки не менше п’яти разів через кожні 10 К.
3. Побудувати графік залежності видовження зразка від температури. Визначити коефіцієнт лінійного розширення за формулою:
 ,
,
де  – тангенс кута
– тангенс кута 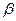 нахилу графіка до горизонтальної осі. Використовуючи графік, визначити похибку визначення
нахилу графіка до горизонтальної осі. Використовуючи графік, визначити похибку визначення 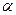 .
.
Контрольні запитання
1. Який фізичний зміст температурного коефіцієнта лінійного розширення?
2. Як з графіка визначити похибку 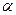 ?
?
Вступ
Звукова хвиля в газі представляє собою періодично повторюваний адіабатний процес стискання та розрідження газу. Швидкість поширення звуку в газі дорівнює:
 , (1)
, (1)
де 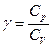 – показник адіабати,
– показник адіабати,  – молярна маса газу,
– молярна маса газу, 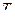 – його термодинамічна температура,
– його термодинамічна температура,  – універсальна газова стала. З формули (1) слідує:
– універсальна газова стала. З формули (1) слідує:
 . (2)
. (2)
Вимірявши швидкість звуку в газі, можна за формулою (2) визначити величину  . В даній роботі швидкість звуку вимірюється методом акустичного резонансу в стовпі повітря, що знаходиться в трубі (рис. 2.11), один кінець якої закритий поршнем 1, а біля другого кінця розташована мембрана динаміка 2. При коливаннях мембрани по трубі поширюється звукова хвиля, яка інтерферує з хвилею, відбитою від поверхні поршня. Як відомо, швидкість хвилі
. В даній роботі швидкість звуку вимірюється методом акустичного резонансу в стовпі повітря, що знаходиться в трубі (рис. 2.11), один кінець якої закритий поршнем 1, а біля другого кінця розташована мембрана динаміка 2. При коливаннях мембрани по трубі поширюється звукова хвиля, яка інтерферує з хвилею, відбитою від поверхні поршня. Як відомо, швидкість хвилі  , частота коливань
, частота коливань 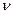 і довжина хвилі
і довжина хвилі  зв’язані співвідношенням:
зв’язані співвідношенням:
 . (3)
. (3)
В трубі можуть збуджуватися власні коливання з різними частотами  ... Якщо частота коливань мембрани співпадає з одною з цих частот, то в трубі встановлюються стоячі хвилі і настає різке підсилення звуку (резонанс). Переміщаючи поршень, можна знайти таке положення, при якому виникає резонанс звуку. При кожному подальшому переміщенні поршня на віддаль
... Якщо частота коливань мембрани співпадає з одною з цих частот, то в трубі встановлюються стоячі хвилі і настає різке підсилення звуку (резонанс). Переміщаючи поршень, можна знайти таке положення, при якому виникає резонанс звуку. При кожному подальшому переміщенні поршня на віддаль  резонанс знову повторюється. Віддаль між сусідніми положеннями поршня, що відповідають резонансу, дає половину довжини звукової хвилі. Знаючи частоту
резонанс знову повторюється. Віддаль між сусідніми положеннями поршня, що відповідають резонансу, дає половину довжини звукової хвилі. Знаючи частоту  , можна визначити за формулою (3) швидкість звуку.
, можна визначити за формулою (3) швидкість звуку.
Опис установки
Поршень 1 переміщається за допомогою штока (3), на якому нанесена шкала (рис 2.11). Коливання мембрани збуджуються звуковим генератором 4. В поршень вмонтований п’єзоелектричний датчик 5, що перетворює механічні коливання в електричні. З датчика напруга подається на вертикальний вхід осцилографа 6. Амплітуда зміщення електронного променя на екрані осцилографа у випадку резонансу досягає найбільшого значення.
Завдання:
|
|
Рис. 2.11
При різних частотах звукових коливань звукового генератора знайти положення поршня, при якому виникає резонанс. Знайти довжину хвилі, а тоді визначити швидкість звуку і величину  . Температуру прийняти рівною кімнатній. Визначити швидкість звуку в повітрі при 0°C. Визначити похибки.
. Температуру прийняти рівною кімнатній. Визначити швидкість звуку в повітрі при 0°C. Визначити похибки.
Контрольні запитання
1. В чому полягає явище резонансу?
2. Що представляє собою стояча хвиля?
3. Що таке власна частота коливань?
ТАБЛИЦІ ФІЗИЧНИХ ВЕЛИЧИН
Основні фізичні постійні
| Фізична величина | Числове значення |
| Швидкість поширення світла у вакуумі | с=2,99792458 м/с |
| Прискорення вільного падіння | g=9,80665 м/с2 |
| Гравітаційна стала | G=6,672·10-11 м3/кг с2 |
| Cтала Авогадро | NA=6,022045·1023 моль-1 |
| Стала Больцмана | k=1,380662·10-23 Дж/К |
| Універсальна газова постійна | R=8,31 Дж/моль·К |
| Елементарний заряд (заряд електрона) | e=1,6021892·10-19 Кл |
| Маса спокою електрона | me=9,10534·10-31 кг |
| Маса спокою протона | mp=1,67226485·10-27 кг |
| Маса спокою нейтрона | mn=1,6749543·10-27 кг |
| Стала Планка | h=6,626176·10-34 Дж·с |
| Електрична стала | ε0=8,85418782·10-12 Ф/м |
| Магнітна стала | μ0=1,25663706·10-6 Гн/м |
| Нормальний тиск атмосфери | P0=101325 Па |
| Атомна одиниця маси | а. о. м.=1,661·10-27 кг |
Густина твердих речовин
| Речовина | ρ,×103 кг/м3 | Речовина | ρ,×103 кг/м3 |
| Алмаз | 3,5 | Нікелін | 8,8 |
| Алюміній | 2,7 | Нікель | 8,8 |
| Антрацит | 1,5 | Олово | 7,3 |
| Береза (суха) | 0,7 | Парафін | 0,9 |
| Вольфрам | 19,0 | Платина | 21,5 |
| Графіт | 2,1-2,6 | Корок | 0,2 |
| Залізо | 7,8 | Свинець | 11,3 |
| Золото | 19,3 | Срібло | 10,5 |
| Цегла | 1,8 | Сталь | 7,9 |
| Латунь | 8,5 | Скло | 2,5 |
| Лід | 0,9 | Цинк | 7,1 |
| Мідь | 8,9 | Чавун | 7,0 |
| Мармур | 2,7 | Ебоніт | 1,8 |
Густина рідин
| Речовина | ρ,×103 кг/м3 | Речовина | ρ,×103 кг/м3 |
| Бензин | 0,7 | Молоко | 1,03 |
| Вода (4°С) | 1,00 | Ртуть (0°С) | 13,6 |
| Вода морська | 1,03 | Скипидар | 0,87 |
| Гліцерин | 1,26 | Спирт | 0,80 |
| Гас | 0,80 | Ефір | 0,72 |
Густина газів
| Речовина | ρ, кг/м3 | Речовина | ρ, кг/м3 |
| Азот | 1,25 | Кисень | 1,43 |
| Повітря | 1,29 | Неон | 0,90 |
| Водень | 0,09 | Вуглекислий газ | 1,98 |
| Гелій | 0,18 | Хлор | 3,21 |
Теплові властивості речовин
| Речовина | Питома теплоємність С, ×103Дж/кг К | Температура плавлення, °С | Питома теплота плавлення С, ×103Дж/кг |
| Алюміній | 0,88 | 660 | 380 |
| Лід | 2,1 | 0 | 330 |
| Мідь | 0,38 | 1083 | 180 |
| Олово | 0,23 | 232 | 59 |
| Свинець | 0,13 | 327 | 25 |
| Срібло | 0,23 | 960 | 87 |
| Сталь | 0,46 | 1400 | 82 |
Кратних одиниць та їх назв
| Множник | Префікс | Позначення префікса |
| 1018 | екса | Е |
| 1015 | пета | П |
| 1012 | тера | Т |
| 109 | гіга | Г |
| 106 | мега | М |
| 103 | кіло | к |
| 102 | гекто | г |
| 10–1 | деци | д |
| 10–2 | санти | с |
| 10–3 | мілі | м |
| 10–6 | мікро | мк |
| 10–9 | нано | н |
| 10–12 | піко | п |
| 10–15 | фемто | ф |
| 10–18 | атто | а |
ЛІТЕРАТУРА
Ч.2. Основи молекулярної фізики та термодинаміки., УПІ, 1994.
Ч.4. Коливання та хвилі., УАД, 1995.
ЧАСТИНА 1. ВСТУП ДО ЛАБОРАТОРНИХ РОБІТ
Последнее изменение этой страницы: 2019-04-10; Просмотров: 369; Нарушение авторского права страницы