ГЛАВА 2. Предел и непрерывность функции одной переменной
Б. Теорема о пределе суперпозиции
Теорема (о пределе суперпозиции). Пусть функция 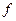 определена на множестве
определена на множестве  ,
, 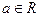 – точка сгущения множества
– точка сгущения множества  и существует предел
и существует предел
 . .
| (2)
|
Пусть, кроме того, функция  определена на множестве
определена на множестве  ,
,  – точка сгущения множества
– точка сгущения множества 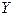 и существует предел.
и существует предел.
 . .
| (3)
|
Тогда, если  , то на множестве
, то на множестве  имеет смысл суперпозиция
имеет смысл суперпозиция  и существует предел.
и существует предел.
 . .
| (4)
|
Д о к а з а т е л ь с т в о. Выберем произвольную окрестность  точки
точки  . Тогда, в силу равенства (3), найдется окрестность
. Тогда, в силу равенства (3), найдется окрестность  точки
точки  такая, что
такая, что

| (5)
|
В свою очередь, в силу равенства (2), для окрестности  точки
точки 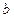 найдется такая окрестность
найдется такая окрестность 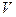 точки
точки  , что
, что
 ,
,
а так как  и по условию
и по условию 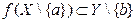 , то отсюда следует, что
, то отсюда следует, что
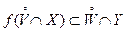 . .
| (6)
|
Из включений (5) и (6) следует, что
 .
.
Таким образом, для произвольно выбранной окрестности  точки
точки  нашлась такая окрестность
нашлась такая окрестность  точки
точки  , что
, что  . По определению предела это и означает, что имеет место равенство (4) □
. По определению предела это и означает, что имеет место равенство (4) □
Односторонние пределы
Пусть  - точка сгущения множества
- точка сгущения множества  . Тогда она является точкой сгущения, по крайней мере, одного из множеств
. Тогда она является точкой сгущения, по крайней мере, одного из множеств

и

Вместе с тем, точкой сгущения обоих этих множеств, одновременно, она может и не быть, так как одно из них может быть, например, пустым.
Пусть  . Положим
. Положим  и
и  .
.
Определение 1. Пусть  - точка сгущения множества
- точка сгущения множества  (соотв.,
(соотв., 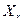 ). Если существует предел
). Если существует предел  (соотв.,
(соотв.,  ), то он называется левосторонним (соотв., правосторонним) пределом функции
), то он называется левосторонним (соотв., правосторонним) пределом функции  в точке
в точке  , или также пределом функции
, или также пределом функции  при
при 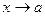 слева (соотв., при
слева (соотв., при  справа).
справа).
В отличие от левостороннего и правостороннего пределов «обычный» предел функции  при
при 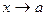 называется иногда двусторонним.
называется иногда двусторонним.
Левосторонний предел функции  в точке
в точке  обозначается обычно одним из символов
обозначается обычно одним из символов
 или
или  ,
,
а правосторонний, соответственно, – одним из символов
 или
или  ..
..
Замечание 1. Поскольку односторонние пределы являются в то же время и обычными пределами, то для них справедливы все теоремы, которые устанавливаются для обычных двусторонних пределов.
Теорема 1. Пусть  ,
,  и
и  – точка сгущения каждого из множеств
– точка сгущения каждого из множеств  и
и 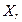 . Тогда, если существуют равные между собой односторонние пределы
. Тогда, если существуют равные между собой односторонние пределы  и
и 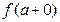 , то существует и равный им двусторонний предел
, то существует и равный им двусторонний предел
 =
=  =
=  .
.
Д о к а з а т е л ь с т в о. Прежде всего заметим, что пересечение любых двух окрестностей точки  является окрестностью этой точки.
является окрестностью этой точки.
Пусть
 =
=  =
= 
и  - произвольная окрестность точки
- произвольная окрестность точки  .
.
По определению  имеем:
имеем:  - окрестность точки точки
- окрестность точки точки  такая, что
такая, что

| (1)
|
Аналогично, по определению  имеем:
имеем: 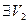 - окрестность точки
- окрестность точки  такая, что
такая, что
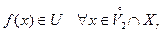
| (2)
|
Рассмотрим теперь следующую окрестность точки  :
:  . Очевидно,
. Очевидно,
 и
и  .
.
Следовательно,
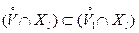 ,
,
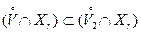
и, кроме того, ясно, что
 .
.
Поэтому из (1) и (2) следует, что
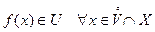
В силу произвольности выбранной окрестности  точки
точки  , это и означает, что
, это и означает, что  □
□
§4. Расширение понятия предела: бесконечные пределы и пределы в бесконечности
Определения. 1. Окрестностью точки  в
в  называется всякое множество
называется всякое множество  , которое содержит некоторую
, которое содержит некоторую  -окрестность
-окрестность  этой точки.
этой точки.
2. Окрестностью точки  в
в  называется любой промежуток вида
называется любой промежуток вида  , где
, где  .
.
3. Окрестностью точки  в
в  называется любой промежуток вида
называется любой промежуток вида  , где
, где  .
.
4. Пусть  и
и  –окрестность этой точки (в
–окрестность этой точки (в  ). Тогда множество
). Тогда множество

называется проколотой окрестностью точки  .
.
5. Точка 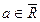 называется точкой сгущения множества
называется точкой сгущения множества  , если для любой окрестности
, если для любой окрестности  этой точки
этой точки
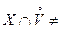 Æ.
Æ.
Теперь естественным образом можно расширить понятие предела  для случая, когда обе или одна из точек
для случая, когда обе или одна из точек  и
и  являются бесконечными точками расширенной числовой оси
являются бесконечными точками расширенной числовой оси  . Соответствующее определение почти дословно повторяет определение 2” из §1.
. Соответствующее определение почти дословно повторяет определение 2” из §1.
Определение 6. Пусть 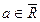 – точка сгущения множества
– точка сгущения множества  и функция
и функция  определена на множестве
определена на множестве  . Конечное или бесконечное число (точка)
. Конечное или бесконечное число (точка) 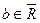 называется пределом функции
называется пределом функции  при
при  (или в точке
(или в точке  ), если для любой окрестности
), если для любой окрестности  точки
точки  (в
(в  ) существует такая окрестность
) существует такая окрестность  точки
точки  (в
(в  ), что
), что
 .
.
Замечание 1. Для различных типов точек 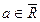 и
и  определение 5 можно детализировать с учетом определения окрестностей для соответствующих типов точек. Например, равенство
определение 5 можно детализировать с учетом определения окрестностей для соответствующих типов точек. Например, равенство 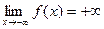 означает, что
означает, что  такое, что
такое, что 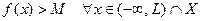 .
.
Упражнение 1. По аналогии с тем, как это сделано в замечании 2, сформулировать, что означает
А)  ,
,
Б)  ,
,
В)  ,
,
Г)  (
(  ),
),
Д)  (
(  ),
),
Е)  (
(  ),
),
Ж)  (
( 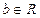 ).
).
Замечание 2. Если существуют пределы функции  как при
как при  , так и при
, так и при  , причем
, причем

 ,
,
то пишут
 .
.
§5. Бесконечно малые и бесконечно большие функции.
Определение 1. Пусть функция  определена на множестве
определена на множестве  и
и  - его точка сгущения. Функция
- его точка сгущения. Функция  называется бесконечно малой при
называется бесконечно малой при  если
если 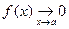 .
.
Упражнения. 1. Покажите, что  - бесконечно малая функция при
- бесконечно малая функция при  .
.
2. Докажите, что функция  - бесконечно малая при
- бесконечно малая при  в том и только том случае, если функция
в том и только том случае, если функция 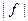 - бесконечно малая при
- бесконечно малая при  .
.
Следующая теорема является простым следствием теоремы о пределе суммы.
Теорема 1. Сумма любого конечного числа бесконечно малых при  функций есть бесконечно малая при
функций есть бесконечно малая при  функция.
функция.
Теорема 2. Произведение бесконечно малой при  функции
функции  и ограниченной в окрестности точки
и ограниченной в окрестности точки  функции
функции  является бесконечно малой при
является бесконечно малой при  функцией.
функцией.
Замечание 1. Точнее в этой теореме предполагается, что функция 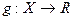 ограничена на множестве
ограничена на множестве  , где
, где  – некоторая окрестность точки
– некоторая окрестность точки  , которая является точкой сгущения множества
, которая является точкой сгущения множества  (это же множество, без ущерба для общности, можно считать и областью определения функции
(это же множество, без ущерба для общности, можно считать и областью определения функции  ).
).
С учетом определения предела функции по Гейне, эта теорема является прямым следствием аналогичной теоремы для числовых последовательностей (теоремы о произведении бесконечно малой последовательности на ограниченную последовательность).
Определение 2. Пусть  – точка сгущения множества
– точка сгущения множества  . Функция
. Функция  называется бесконечно большой при
называется бесконечно большой при  , если
, если  .
.
Теорема 3 (о связи между бесконечно малыми и бесконечно большими). Пусть  - точка сгущения множества
- точка сгущения множества  и
и  на
на  (или, хотя бы, в некоторой окрестности точки
(или, хотя бы, в некоторой окрестности точки  ). Тогда
). Тогда
1) если  – бесконечно малая при
– бесконечно малая при  функция, то
функция, то  – бесконечно большая при
– бесконечно большая при  функция;
функция;
2) если же  – бесконечно большая при
– бесконечно большая при  функция, то
функция, то  – бесконечно малая при
– бесконечно малая при  функция.
функция.
Д о к а з а т е л ь с т в о. 1) Выберем произвольное  и положим
и положим  . Так как
. Так как  , то найдется такая окрестность
, то найдется такая окрестность  точки
точки  , что
, что
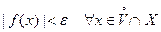
и, следовательно,  . В силу произвольности
. В силу произвольности  это и означает, что
это и означает, что  – бесконечно большая при
– бесконечно большая при  функция.
функция.
2) Возьмем произвольное 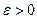 и положим
и положим  . Поскольку
. Поскольку  , то найдется такая окрестность
, то найдется такая окрестность  точки
точки  , что
, что
 ,
,
Поэтому  , т.е. то
, т.е. то  – бесконечно малая при
– бесконечно малая при  функция □
функция □
§6. Символы «о» и «О». Эквивалентные при  функции.
функции.
Пусть функции  и
и  определены на множестве
определены на множестве  и
и  – точка сгущения множества
– точка сгущения множества  . Пусть также в некоторой проколотой окрестности
. Пусть также в некоторой проколотой окрестности 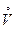 точки
точки  функция
функция  отлична от нуля (точнее,
отлична от нуля (точнее,  ). Там где это ниже необходимо по смыслу, будем также считать, что в той же проколотой окрестности отлична от нуля и функция
). Там где это ниже необходимо по смыслу, будем также считать, что в той же проколотой окрестности отлична от нуля и функция  .
.
Определения: 1. Если
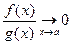 ,
,
то говорят, что функция  есть о-малое от функции
есть о-малое от функции  при
при  , и пишут
, и пишут
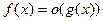 при
при  .
.
2. Если функция  ограничена в некоторой проколотой окрестности
ограничена в некоторой проколотой окрестности  точки
точки  , т.е. если она ограничена на множестве
, т.е. если она ограничена на множестве  , то говорят, что функция
, то говорят, что функция  есть о-большое от функции
есть о-большое от функции  при
при  , и пишут
, и пишут
 при
при  .
.
3. Говорят, что функции  и
и  одного порядка при
одного порядка при  , если
, если
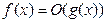 и
и  при
при  .
.
4. Говорят, что функции  и
и  асимптотически равны при
асимптотически равны при  , если
, если
 .
.
Замечания: 1. Как следует из определений 1 и 2, соответственно, запись 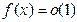 (при
(при  ) означает, что функция
) означает, что функция  – бесконечно малая при
– бесконечно малая при  , а запись
, а запись  (при
(при  ) означает, что функция
) означает, что функция  ограничена в окрестности точки
ограничена в окрестности точки  .
.
2. Если 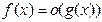 при
при  , то в силу теоремы о локальной ограниченности функции, имеющей (конечный) предел, тем более
, то в силу теоремы о локальной ограниченности функции, имеющей (конечный) предел, тем более 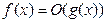 при
при  .
.
Упражнение 1. Покажите, что (функции  и
и  – функции одного порядка) ⇔ (
– функции одного порядка) ⇔ ( 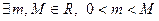 ,
, 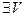 - окрестность точки
- окрестность точки  , что
, что 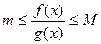 при
при  ).
).
Определения: 5. Пусть  и
и  – бесконечно малые при
– бесконечно малые при  функции. Функция
функции. Функция  называется бесконечно малой высшего порядка по сравнению с функцией
называется бесконечно малой высшего порядка по сравнению с функцией  , если
, если 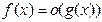 при
при  .
.
6. Если бесконечно малые при  функции
функции  и
и  асимптотически равны, то говорят, что они эквивалентны при
асимптотически равны, то говорят, что они эквивалентны при  , при этом пишут
, при этом пишут  ~
~  (
(  ).
).
Теорема 1. Пусть 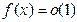 и
и  при
при  . Тогда
. Тогда
[  ~
~  (
(  )] ⇔ [
)] ⇔ [  ≜
≜  при
при  ]
]
Д о к а з а т е л ь с т в о. Необходимость (⇒). Так как  ~
~  (
(  ), то
), то
 ,
,
т.е.  при
при  .
.
Достаточность (⇐). Поскольку  при
при  , то
, то
 ,
,
т.е.  ~
~  (
(  ) □
) □
Теорема 2. Пусть 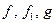 и
и  – бесконечно малые при
– бесконечно малые при  функции, причем
функции, причем  ~
~  , а
, а  ~
~  при
при  . Тогда если
. Тогда если
 ,
,
то и
 .
.
Замечание 3. Иными словами в этой теореме утверждается, что при отыскании предела частного бесконечно малых функций, каждую из этих бесконечно малых можно заменить на эквивалентную бесконечно малую.
Д о к а з а т е л ь с т в о теоремы 2. Поскольку

и по условию
 ,
,
 ,
,
 ,
,
то по теореме о пределе частного имеем
 □
□
По аналогии с определениями 5 и 6 вводятся следующие определения для бесконечно больших функций.
Определения: 7. Пусть  и
и  – бесконечно большие при
– бесконечно большие при  функции. Функция
функции. Функция  называется бесконечно большой высшего порядка по сравнению с функцией
называется бесконечно большой высшего порядка по сравнению с функцией  , если
, если  – бесконечно большая при
– бесконечно большая при  функция, т.е. если
функция, т.е. если  при
при  .
.
8. Если бесконечно большие при  функции
функции  и
и  асимптотически равны при
асимптотически равны при  , то говорят, что они эквивалентны при
, то говорят, что они эквивалентны при  .
.
Замечание 4. Теоремы 1 и 2 при надлежащих изменениях сохраняют свою силу для бесконечно больших функций.
Определение 9. Пусть  и
и  – бесконечно малые (бесконечно большие) при
– бесконечно малые (бесконечно большие) при  функции. Если
функции. Если  и функции
и функции 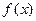 и
и  одного порядка при
одного порядка при  (здесь
(здесь 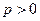 ), то говорят, что
), то говорят, что  – бесконечно малая (бесконечно большая) порядка
– бесконечно малая (бесконечно большая) порядка  по сравнению
по сравнению  .
.
Определение 10. Пусть  и
и  – бесконечно малые (бесконечно большие) при
– бесконечно малые (бесконечно большие) при  функции. Если
функции. Если 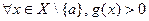 и
и 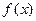 ~
~ 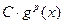 при
при  , то говорят, что функция
, то говорят, что функция 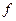 (при сравнении с
(при сравнении с  ) имеет главную часть
) имеет главную часть 
Понятие непрерывной функции
Определение 1. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любого
, если для любого  существует такое
существует такое  , что для любого
, что для любого  , удовлетворяющего неравенству
, удовлетворяющего неравенству
 , ,
| (1)
|
справедливо также и неравенство

| (2)
|
Замечание 1. Данное определение иногда называется определением непрерывности функции на языке  . По форме оно явно напоминает определение предела функции в форме Коши, при этом в отличие от него здесь требуется, чтобы точка
. По форме оно явно напоминает определение предела функции в форме Коши, при этом в отличие от него здесь требуется, чтобы точка  принадлежала множеству
принадлежала множеству  , но не требуется, чтобы она была точкой сгущения этого множества.
, но не требуется, чтобы она была точкой сгущения этого множества.
В связи с последним замечанием отметим, что если точка  не является точкой сгущения множества
не является точкой сгущения множества  , то она называется изолированной точкой этого множества. Иными словами точка
, то она называется изолированной точкой этого множества. Иными словами точка  называется изолированной точкой множества
называется изолированной точкой множества  , если существует такая ее окрестность
, если существует такая ее окрестность  , что
, что 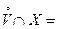 Æ или, что тоже самое,
Æ или, что тоже самое,  .
.
Замечание 2. Согласно определению 1 в любой изолированной точке своей области определения всякая функция является непрерывной. Действительно, каково бы ни было  по определению изолированной точки можно выбрать столь малое
по определению изолированной точки можно выбрать столь малое  , что
, что  и, следовательно, при этом
и, следовательно, при этом  среди точек множества
среди точек множества  неравенству (1) будет удовлетворять только точка
неравенству (1) будет удовлетворять только точка  , но для
, но для 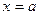 неравенство (2) очевидно выполняется для любой функции
неравенство (2) очевидно выполняется для любой функции  .
.
Замечание 3. В силу того, что для  неравенство (2) выполняется очевидным образом, можно заключить, что в том случае, когда точка
неравенство (2) выполняется очевидным образом, можно заключить, что в том случае, когда точка  является точкой сгущения множества
является точкой сгущения множества  , неравенство (1) можно заменить неравенствами:
, неравенство (1) можно заменить неравенствами:  , при этом определение 1 превратится в определение предела
, при этом определение 1 превратится в определение предела  при
при  . Таким образом, можно сказать, что если точка
. Таким образом, можно сказать, что если точка  является точкой сгущения множества
является точкой сгущения множества  , то функция
, то функция  будет непрерывной в этой точке в том и только том, случае, когда
будет непрерывной в этой точке в том и только том, случае, когда  .
.
Замечание 4. На языке окрестностей определение 1 можно переформулировать следующим образом:
Определение 1’. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любого
, если для любого  существует такое
существует такое  , что
, что
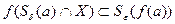
(т.е.  ).
).
Это определение, а значит и определение 1, очевидно равносильно следующему определению:
Определение 1”. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любой окрестности
, если для любой окрестности  точки
точки 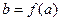 существует такая окрестность
существует такая окрестность  точки
точки  , что
, что
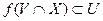 .
.
С учетом замечаний 2 и 3, теоремы о равносильности определений предела по Коши и по Гейне, а также с учетом того, что всякую точку  можно представить в виде
можно представить в виде 
 ,*) заключаем, что определения 1 и 1’ равносильны следующему определению:
,*) заключаем, что определения 1 и 1’ равносильны следующему определению:
Определение 2. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любой последовательности точек
, если для любой последовательности точек  ,
,  , последовательность
, последовательность 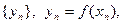 сходится и
сходится и
 .
.
Как будет показано далее все элементарные функции являются непрерывными в своих областях определения. В связи с этим напомним, что к числу, так называемых, основных элементарных функций относятся:
– постоянная функция: 
– степенная функция:  ;
;
– показательная функция:  ;
;
– логарифмическая функция: 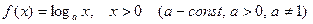 ;
;
– тригонометрические функции:
 ;
;
– обратные тригонометрические функции:
 .
.
В свою очередь, элементарной называется всякая функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических операций и образования суперпозиций.
Теорема 1 (О непрерывности сужения). Пусть функция  непрерывна в точке
непрерывна в точке  и
и 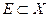 причем
причем  . Тогда функция
. Тогда функция  также непрерывна в точке
также непрерывна в точке  .
.
Д о к а з а т е л ь с т в о вытекает из определения сужения и определения непрерывности.
Теорема 2 (Арифметические свойства непрерывных функций). Пусть функции  и
и  определены на множестве
определены на множестве  и непрерывны в точке
и непрерывны в точке  . Тогда и функции:
. Тогда и функции:
 ,
, 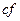
 ,
, 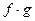 ,
, 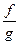 (при
(при  на
на  )
)
непрерывны в точке 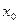 .
.
Теорема 3 (О локальной ограниченности). Пусть функция  определена на множестве
определена на множестве  и непрерывна в точке
и непрерывна в точке  . Тогда существует такая окрестность
. Тогда существует такая окрестность  точки
точки  , что функция
, что функция  ограничена на множестве
ограничена на множестве  .
.
Теорема 4 (О стабилизации знака). Пусть функция  определена на множестве
определена на множестве  и непрерывна в точке
и непрерывна в точке  . Тогда если
. Тогда если  , то существует такая окрестность
, то существует такая окрестность  точки
точки  , что
, что 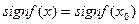
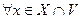 .
.
Наконец отметим еще две простые теоремы
Теорема 5. Пусть функция  определена на множестве
определена на множестве 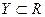 и непрерывна в точке, а функция
и непрерывна в точке, а функция  определена на множестве
определена на множестве  и непрерывна в точке
и непрерывна в точке  , причем
, причем  и
и  . Тогда сложная функция
. Тогда сложная функция  непрерывна в точке
непрерывна в точке 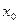 .
.
Д о к а з а т е л ь с т в о. Выберем произвольную последовательность  ,
,  . Так как
. Так как  - непрерывна в точке
- непрерывна в точке 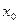 , то
, то
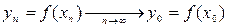 ,
,
а так как  , то
, то  . Поэтому, в силу непрерывности функции
. Поэтому, в силу непрерывности функции  в точке
в точке  , имеем
, имеем
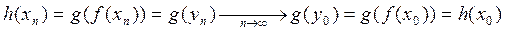 ,
,
то есть
 ,
,
что и означает, что функция  - непрерывна в точке
- непрерывна в точке 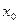 .
.
Пусть функция  определена на множестве
определена на множестве  и
и  . Рассмотрим множества:
. Рассмотрим множества:


Определение 1. Функция  называется непрерывной слева (непрерывной справа) в точке
называется непрерывной слева (непрерывной справа) в точке  , если функция
, если функция  (соответственно
(соответственно  ) непрерывна в точке
) непрерывна в точке  .
.
Замечание. На языке  определение, например, непрерывности слева, формулируется следующим образом: функция
определение, например, непрерывности слева, формулируется следующим образом: функция  называется непрерывной слева в точке
называется непрерывной слева в точке  , если
, если 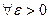
 такое, что
такое, что  удовлетворяющего неравенствам
удовлетворяющего неравенствам

справедливо неравенство
 .
.
Теорема 6. Функция  непрерывна в точке
непрерывна в точке 
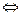 она непрерывна в ней слева и справа одновременно.
она непрерывна в ней слева и справа одновременно.
Если  - изолированная точка множества
- изолированная точка множества  , то утверждение очевидно. Если же
, то утверждение очевидно. Если же  - точка сгущения множества
- точка сгущения множества  , то оно вытекает из аналогичной теоремы об односторонних пределах.
, то оно вытекает из аналогичной теоремы об односторонних пределах.
§9. Точки разрыва функции. Классификация точек разрыва.
Определение 1. Пусть функция  определена на множестве
определена на множестве  и
и  . Если функция
. Если функция  непрерывна в точке
непрерывна в точке  , то она называется точкой непрерывности функции
, то она называется точкой непрерывности функции  . В противном случае, точка
. В противном случае, точка  называется точкой разрыва функции
называется точкой разрыва функции  .
.
Замечание 1. Так как всякая изолированная точка множества  является точкой непрерывности определенной на нем функции
является точкой непрерывности определенной на нем функции  , то точками разрыва могут быть только точки сгущения множества
, то точками разрыва могут быть только точки сгущения множества  .
.
Замечание 2. Если  – точка разрыва функции
– точка разрыва функции  , то либо предел
, то либо предел  не существует, либо он существует, но
не существует, либо он существует, но  .
.
Определение 2. Точка разрыва 1-го рода называется точкой устранимого разрыва функции  , если в ней существует предел функции
, если в ней существует предел функции  , но он не равен ее значению в этой точке.
, но он не равен ее значению в этой точке.
Замечание 4. Если точка  – точка устранимого разрыва функции
– точка устранимого разрыва функции  , то изменив ее значение в этой точке на значение, равное величине предела в этой точке, получим непрерывную функцию в этой точке
, то изменив ее значение в этой точке на значение, равное величине предела в этой точке, получим непрерывную функцию в этой точке
 .
.
Этим и объясняется термин точка устранимого разрыва.
В следующих двух определениях предполагается, что точка  принадлежит области определения функции
принадлежит области определения функции  вместе с некоторой своей окрестностью
вместе с некоторой своей окрестностью  .
.
Определение 3. Пусть  – точка разрыва функции
– точка разрыва функции  . Если оба односторонних предела
. Если оба односторонних предела  и
и  существуют и конечны, то она называется точкой разрыва 1-го рода
существуют и конечны, то она называется точкой разрыва 1-го рода
Определение 4. Точка разрыва функции называется точкой разрыва 2-го рода, если она не является точкой разрыва 1-го рода.
Замечание 3. Иными словами точка разрыва функции является точкой разрыва 2-го рода, если в ней хотя бы один из односторонних пределов не существует, либо является бесконечным.
Проиллюстрируем данные выше определения на некоторых примерах.
Пример 1 (всюду разрывной функции). Функция Дирихле, определенная на всей числовой оси равенствами:
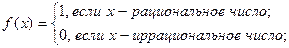
является разрывной в каждой точке  . Действительно, для любой последовательности рациональных чисел
. Действительно, для любой последовательности рациональных чисел  , сходящейся к точке
, сходящейся к точке  , имеем
, имеем  , а для любой последовательности иррациональных чисел
, а для любой последовательности иррациональных чисел 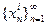 ,
,  , в свою очередь, имеем
, в свою очередь, имеем  . Следовательно, ни в одной точке
. Следовательно, ни в одной точке 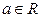 не существует предел
не существует предел  и, следовательно каждая точка
и, следовательно каждая точка  – точка разрыва функции Дирихле. Более того, нетрудно видеть, что ни в одной точке
– точка разрыва функции Дирихле. Более того, нетрудно видеть, что ни в одной точке  не существуют оба односторонних придела
не существуют оба односторонних придела  и
и  , так как описанные выше последовательности
, так как описанные выше последовательности  и
и  , с одной стороны, можно выбрать так, что
, с одной стороны, можно выбрать так, что  , а с другой стороны, можно выбрать и так, что
, а с другой стороны, можно выбрать и так, что  . Таким образом, каждая точка
. Таким образом, каждая точка 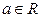 – точка разрыва 2-го рода функции Дирихле.
– точка разрыва 2-го рода функции Дирихле.
Пример 2. Функция «сигнум  »
»

очевидно, разрывна в точке  , причем эта точка – точка разрыва 1-го рода.
, причем эта точка – точка разрыва 1-го рода.
Пример 3. Функция  разрывна в точке
разрывна в точке  , которая, очевидно, является точкой устранимого разрыва.
, которая, очевидно, является точкой устранимого разрыва.
Формула Тейлора.
n.1. Формула Тейлора для многочлена.
Глава 1 Рассмотрим некоторый многочлен степени  с вещественными коэффициентами:
с вещественными коэффициентами:
Глава 2  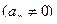
| Глава 3 (1)
|
Зададим произвольное вещественное число  и в правой части равенства (1) представим
и в правой части равенства (1) представим 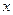 в виде
в виде  :
:

Раскрыв здесь квадратные скобки и приведя подобные члены при одинаковых степенях  , в результате получим разложение многочлена (1) по степеням
, в результате получим разложение многочлена (1) по степеням  :
:
 , ,
| (2)
|
где 
 - постоянные, зависящие от исходных коэффициентов и от числа
- постоянные, зависящие от исходных коэффициентов и от числа  .
.
При больших  , на практике, указанный выше способ разложения многочлена по степеням
, на практике, указанный выше способ разложения многочлена по степеням  весьма трудоемок. Оказывается, имеется простой способ отыскания коэффициентов
весьма трудоемок. Оказывается, имеется простой способ отыскания коэффициентов 
 разложения многочлена по степеням
разложения многочлена по степеням  . Будем последовательно дифференцировать равенство (2):
. Будем последовательно дифференцировать равенство (2):

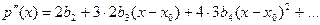
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
 .
.
Полагая в каждом из этих равенств  получим
получим


. . . . . . . . .
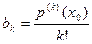
. . . . . . . . .
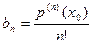
Если кроме того положить  в (2), то считая, как обычно,
в (2), то считая, как обычно,  и
и  будем также иметь
будем также иметь

Таким образом, для коэффициентов разложения (2) многочлена по степеням имеем следующие формулы
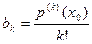 , , 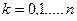
| (3)
|
В итоге заключаем, что разложение (2) можно записать в виде (4):

| (4)
|
Формула (4) называется формулой Тейлора по степеням 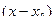 для многочлена
для многочлена  степени
степени  . Из вывода этой формулы следует, что разложение многочлена по степеням
. Из вывода этой формулы следует, что разложение многочлена по степеням  является единственным, так как коэффициенты любого такого разложения однозначно определяются по формулам (3).
является единственным, так как коэффициенты любого такого разложения однозначно определяются по формулам (3).
Формулу Тейлора по степеням  для многочлена
для многочлена  , то есть формулу
, то есть формулу

называют также формулой Маклорена.
n.2. Локальная формула Тейлора.
Пусть функция 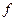
 раз дифференцируема в точке
раз дифференцируема в точке  . Напомним, это означает, что существует такая окрестность
. Напомним, это означает, что существует такая окрестность  точки
точки  , в которой определена сама функция
, в которой определена сама функция  и существуют конечные производные
и существуют конечные производные


при этом в точке  существует также конечная производная
существует также конечная производная  . Поэтому, в частности, определен многочлен
. Поэтому, в частности, определен многочлен
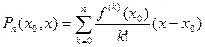 ,
,
называемый (  -ым) многочленом Тейлора функции
-ым) многочленом Тейлора функции  в точке
в точке  .
.
Положим
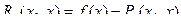
Тогда

Эта формула или, в более явном виде, формула

| (1)
|
называется формулой Тейлора функции в точке  , а функция
, а функция 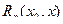 - остаточным членом формулы Тейлора.
- остаточным членом формулы Тейлора.
Ниже будет доказано, что остаточный член формулы Тейлора может быть записан в виде
 (при
(при  ) )
| (2)
|
Остаточный член в такой форме обычно называют остаточным членом в форме Пеано, а формулу Тейлора с остаточным членом в такой форме, т. е. формулу
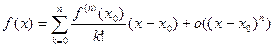
| (3)
|
называют, соответственно, формулой Тейлора с остаточным членом в форме Пеано или, также, локальной формулой Тейлора.
Лемма 1. Пусть функция 
 раз дифференцируема в точке
раз дифференцируема в точке  и
и
 . .
| (4)
|
Тогда
 . .
| (5)
|
Д о к а з а т е л ь с т в о. Докажем утверждение леммы по индукции.
При  в силу дифференцируемости функции
в силу дифференцируемости функции  в точке
в точке  имеем
имеем

А так как по условию (4)
 ,
,
то это означает, что

таким образом, при  утверждение леммы справедливо.
утверждение леммы справедливо.
Предположим, что оно справедливо при 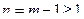 , и покажем, что тогда оно справедливо и при
, и покажем, что тогда оно справедливо и при  .
.
Действительно, поскольку  , то функция
, то функция  имеет в некоторой окрестности
имеет в некоторой окрестности  производную
производную  , и по условию (4) (для
, и по условию (4) (для 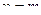 )
)
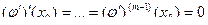
Тогда по индукционному предположению
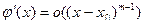
| (6)
|
Далее, так как функция 
 раз дифференцируема в точке
раз дифференцируема в точке  и
и  , то для любой точки
, то для любой точки  из окрестности
из окрестности  , в которой существует конечные производные
, в которой существует конечные производные
 ,
,
Имеет место и формула конечных приращений Лагранжа
 , ,
| (7)
|
где точка  лежит между точками
лежит между точками  и
и  . (Рекомендуется проверить, что на отрезке с концами в точках
. (Рекомендуется проверить, что на отрезке с концами в точках  и
и  функция удовлетворяет всем условиям теоремы Лагранжа).
функция удовлетворяет всем условиям теоремы Лагранжа).
Поскольку по условию  , то из формул (6) и (7) следует, что
, то из формул (6) и (7) следует, что

Полагая здесь

будем иметь

Поэтому равенство (5) при 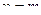 будет доказано, если будет показано, что
будет доказано, если будет показано, что
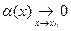
| (8)
|
Действительно, так как точка  лежит между точками
лежит между точками  и
и  , то
, то
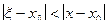
| (9)
|
и, следовательно,

| (10)
|
Остаётся заметить, что в силу (8)  при
при  и, значит,
и, значит,
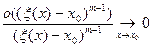
Тогда по принципу двух милиционеров из (10) следует (8)
Теорема 1. Если функция 
 раз дифференцируема в точке
раз дифференцируема в точке  , то для нее имеет место формула Тейлора с остаточным членом в форме Пеано (3).
, то для нее имеет место формула Тейлора с остаточным членом в форме Пеано (3).
Д о к а з а т е л ь с т в о. Достаточно заметить, что при выполнении условий теоремы функция
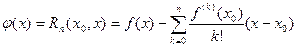
Удовлетворяет условиям леммы 1
Замечание 1. Вот другая, равносильная формулировка теоремы 1: Если функция 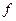 имеет в точке
имеет в точке  конечные производные до порядка
конечные производные до порядка  включительно, то для нее имеет место локальная формула Тейлора (3).
включительно, то для нее имеет место локальная формула Тейлора (3).
nо3. Формула Тейлора с остаточным членом в форме Коши и в форме Лагранжа.
Теорема 2. Пусть на отрезке  с концами в точках
с концами в точках  и
и  функция
функция  и все ее производные до порядка
и все ее производные до порядка  включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная
включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная  . Тогда, для любой непрерывной на этом отрезке функции
. Тогда, для любой непрерывной на этом отрезке функции  , дифференцируемой во внутренних точках этого отрезка и имеющей в каждой из этих точек отличную от нуля производную, существует точка
, дифференцируемой во внутренних точках этого отрезка и имеющей в каждой из этих точек отличную от нуля производную, существует точка  , лежащая между точками
, лежащая между точками  и
и  , такая, что остаточный член в формуле Тейлора может быть записан в виде
, такая, что остаточный член в формуле Тейлора может быть записан в виде
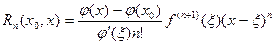 . .
| (1)
|
Д о к а з а т е л ь с т в о. На отрезке  с концами в точках
с концами в точках  и
и  рассмотрим функцию переменной
рассмотрим функцию переменной  :
:
 ,
,
где

 .
.
Из условий теоремы и определения функции 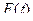 следует, что она непрерывна на отрезке
следует, что она непрерывна на отрезке  и дифференцируема во внутренних точках этого отрезка. По условию теоремы функция
и дифференцируема во внутренних точках этого отрезка. По условию теоремы функция  обладает теми же свойствами.
обладает теми же свойствами.
Таким образом, функции  и
и  на отрезке I удовлетворяют всем условиям теоремы Коши о среднем значении для дифференцируемых функций.
на отрезке I удовлетворяют всем условиям теоремы Коши о среднем значении для дифференцируемых функций.
По этой теореме между точками  и
и  найдется такая точка
найдется такая точка  , что
, что

| (2)
|
Поскольку
 , ,
| (3)
|
то нетрудно видеть, что

 . .
| (4)
|
К тому же, как следует из (3),

| (5)
|
и

| (6)
|
Из формулы (2), (4) – (6) имеем
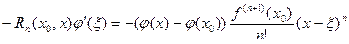
В свою очередь отсюда, с учетом того, что по условию теоремы 
(  - внутренняя точка отрезка
- внутренняя точка отрезка  ), получим искомое равенство (1).
), получим искомое равенство (1).
Следствие. Если на отрезке с концами в точках  и
и  функция
функция  и все ее производные до порядка
и все ее производные до порядка  включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная
включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная  , то остаточный член в формуле Тейлора
, то остаточный член в формуле Тейлора

| (7)
|
может быть записан, как в форме Коши:
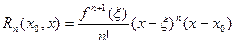 , ,
| (8)
|
так и в форме Лагранжа:

| (9)
|
(здесь  лежит между точками
лежит между точками  и
и  , при этом является, вообще говоря, разной в формулах (8) и (9)).
, при этом является, вообще говоря, разной в формулах (8) и (9)).
Д о к а з а т е л ь с т в о. Формула (8) вытекает из формулы (1), если в ней положить

В свою очередь, формула (9) вытекает из той же формулы (1), если в последней положить

Таким образом, если выполнены условия следствия из теоремы 2, то формулу Тейлора для функции  можно записать как в виде
можно записать как в виде

| (10)
|
(формула Тейлора с остаточным членов в форме Лагранжа),
так и в виде

| (11)
|
(формула Тейлора с остаточным членом в форме Коши).
nо4. Разложение некоторых элементарных функцией по формуле Тейлора.
Если  , то формула Тейлора функции
, то формула Тейлора функции  имеет особенно простой вид:
имеет особенно простой вид:
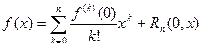
| (1)
|
В этом случае она называется формулой Маклорена. Остаточный член в ней в форме Пеано, Лагранжа и Коши, соответственно, имеет вид
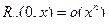 ,
,
 ,
,
и
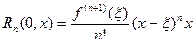
Укажем разложения некоторых элементарных функций по формуле Маклорена.
 . Пусть
. Пусть  . Эта функция имеет производные любого порядка и в любой точке
. Эта функция имеет производные любого порядка и в любой точке  (в таких случаях говорят, что функция бесконечно дифференцируема
(в таких случаях говорят, что функция бесконечно дифференцируема  ).
).
Как известно

Поэтому формула Маклорена функции  имеет вид (
имеет вид (  ):
):
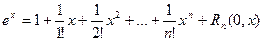
где остаточный член можно записать в любой из форм:
 ( в форме Пеано)
( в форме Пеано)
 ( в форме Лагранжа)
( в форме Лагранжа)
и
 (в форме Коши),
(в форме Коши),
где точка  в каждой из двух последних формул лежит между точками
в каждой из двух последних формул лежит между точками  и
и  .
.
 . Пусть
. Пусть 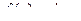 . Так как эта функция бесконечно дифференцируема на всей вещественной оси и
. Так как эта функция бесконечно дифференцируема на всей вещественной оси и
 ,
,
то
 ;
;

и, следовательно,

При этом остаточный член в форме Пеано имеет вид:
 ,
,
соответственно остаточный член в форме Лагранжа выглядит следующим образом:

| (2)
|
а остаточный член в форме Коши имеет вид:

| (3)
|
Замечание 1. Для доказательства, например, равенства (2) достаточно заметить, что остаточный член  в форме Лагранжа в общем случае имеет вид:
в форме Лагранжа в общем случае имеет вид:
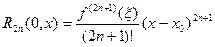
а затем убедиться в том, что для функции  имеют место равенства
имеют место равенства

 . Пусть
. Пусть  . Эта функция также бесконечно дифференцируема
. Эта функция также бесконечно дифференцируема  . Поскольку здесь
. Поскольку здесь
 ,
,
то

Поэтому имеем,
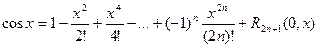
при этом остаточный член имеет вид:

( в форме Пеано);

( в форме Лагранжа);

( в форме Коши).
Приведем без доказательства еще несколько разложений по формуле Маклорена:
 .
. 
 .
. 
 .
. 
ГЛАВА 2. Предел и непрерывность функции одной переменной
§1. Понятие предела числовой функции.
Напомним, что числовой функцией или функцией одной (вещественной) переменной называется отображение  , область определения которой есть числовое множество, т.е.
, область определения которой есть числовое множество, т.е.  .
.
Пусть  и
и  – окрестность точки
– окрестность точки 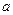 (т.е.
(т.е.  – такое числовое множество, которое содержит некоторую
– такое числовое множество, которое содержит некоторую 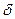 -окрестность
-окрестность  (
(  )точки
)точки  ). Множество
). Множество  далее будем называть проколотой окрестностью точки
далее будем называть проколотой окрестностью точки  .
.
Определение 1. Точка  называется точкой сгущения или предельной точкой множества
называется точкой сгущения или предельной точкой множества  , если в любой ее проколотой окрестности имеется хотя бы одна точка этого множества, т.е. для любой окрестности
, если в любой ее проколотой окрестности имеется хотя бы одна точка этого множества, т.е. для любой окрестности  точки
точки 
 Æ.
Æ.
Определение 2 (предела функции по Коши). Пусть функция  определена на множестве
определена на множестве  и
и  – точка сгущения этого множества. Число
– точка сгущения этого множества. Число  называется пределом функции
называется пределом функции  при
при  или, также, пределом функции
или, также, пределом функции  в точке
в точке  , если для любого
, если для любого  существует такое
существует такое 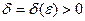 , что для любого
, что для любого 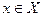 , удовлетворяющего неравенствам:
, удовлетворяющего неравенствам:
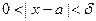
| (1)
|
имеет место неравенство

| (2)
|
Если число  является пределом функции
является пределом функции  в точке
в точке  , то пишут
, то пишут
 , или
, или  , или
, или  .
.
Замечание 3. Определение предела по Коши часто называют определением предела на языке  . На языке окрестностей оно, очевидно, может быть переформулировано следующим образом:
. На языке окрестностей оно, очевидно, может быть переформулировано следующим образом:
Определение 2’. Пусть функция  определена на множестве
определена на множестве  и
и  – точка сгущения этого множества. Число
– точка сгущения этого множества. Число  называется пределом функции
называется пределом функции  при
при  или, также, пределом функции
или, также, пределом функции  в точке
в точке  , если для любого
, если для любого  существует такое
существует такое  , что
, что
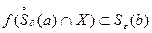
(т.е. 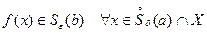 ).
).
В свою очередь, нетрудно видеть, что это определение равносильно следующему определению.
Определение 2”. Пусть функция  определена на множестве
определена на множестве  и
и  – точка сгущения этого множества. Число
– точка сгущения этого множества. Число  называется пределом функции
называется пределом функции  при
при  или, также, пределом функции
или, также, пределом функции  в точке
в точке  , если для любой окрестности
, если для любой окрестности 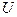 точки
точки 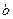 существует такая окрестность
существует такая окрестность  точки
точки  , что
, что
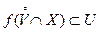 .
.
Определение 3 (предела по Гейне). Пусть функция  определена на множестве
определена на множестве  и
и  – точка сгущения этого множества. Число
– точка сгущения этого множества. Число  называется пределом функции
называется пределом функции  при
при  или, также, пределом функции
или, также, пределом функции  в точке
в точке  , если для любой последовательности
, если для любой последовательности  последовательность
последовательность  сходится и
сходится и
 . .
| (3)
|
Замечание 4. Последнее определение называют также определением предела функции на языке последовательностей.
Теорема 1. Определения предела функции по Коши и по Гейне равносильны.
Д о к а з а т е л ь с т в о. Требуется доказать, что если число  является пределом функции
является пределом функции  при
при  в смысле одного из определений 2 и 3, то оно является также и ее пределом в точке
в смысле одного из определений 2 и 3, то оно является также и ее пределом в точке  (точке сгущения множества
(точке сгущения множества  ) и в смысле другого из этих определений.
) и в смысле другого из этих определений.
Пусть
 (в смысле Коши)
(в смысле Коши)
| (4)
|
Выберем произвольную последовательность

и произвольное  . В силу условия (4) и определения 2 найдется
. В силу условия (4) и определения 2 найдется  такое, что для любого
такое, что для любого  , удовлетворяющего неравенствам (1) имеет место и неравенство (2). В свою очередь, поскольку
, удовлетворяющего неравенствам (1) имеет место и неравенство (2). В свою очередь, поскольку 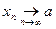 , то для этого
, то для этого  найдется такой номер
найдется такой номер  , что
, что
 ,
,
а так как по условию  и
и 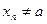
 , то по определению 2
, то по определению 2
  . .
| (5)
|
В силу произвольности  это и означает, что имеет место равенство (3), т.е.
это и означает, что имеет место равенство (3), т.е.
 (в смысле Гейне)
(в смысле Гейне)
| (6)
|
Обратно, пусть имеет место равенство (6). Докажем, что тогда имеет место и равенство (4). Предположим противное. Тогда  :
:
 .
.
Зафиксируем это  . Для него, в частности,
. Для него, в частности,  :
:
 ,
,
при этом очевидно, что 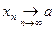 . Таким образом, нашлась последовательность
. Таким образом, нашлась последовательность  такая, что
такая, что

| (7)
|
Однако, для той же последовательности и того же  в силу условия (6), определения 3 и определения предела числовой последовательности найдется такой номер
в силу условия (6), определения 3 и определения предела числовой последовательности найдется такой номер  , что будет иметь место и неравенство (5), противоречащее неравенству (7). Следовательно (6)⇒(4) □
, что будет иметь место и неравенство (5), противоречащее неравенству (7). Следовательно (6)⇒(4) □
Следующие теоремы, с учетом определения предела функции по Гейне являются прямыми следствиями аналогичных теорем о пределе последовательности.
Теорема 2. Если функция  имеет предел в точке
имеет предел в точке  , где
, где  – точка сгущения множества
– точка сгущения множества  , то этот предел единственный.
, то этот предел единственный.
Теорема 3 (об арифметических свойствах предела функции). Пусть функции  и
и  определены на множестве
определены на множестве  и
и  - точка сгущения этого множества. Тогда если существуют пределы
- точка сгущения этого множества. Тогда если существуют пределы
 и
и  ,
,
то существуют и пределы
 ,
,  ,
, 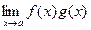 ,
, 
(последний при дополнительном предположении, что и  ),
),
причем
а) 

 ,
,
б) 
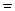


 (теорема о пределе суммы и разности),
(теорема о пределе суммы и разности),
в) 
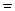

 (теорема о пределе произведения),
(теорема о пределе произведения),
г) 
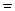
 (теорема о пределе частного).
(теорема о пределе частного).
Теорема 4 (о предельном переходе в неравенстве). Пусть функции  и
и  определены на множестве
определены на множестве  и
и  - точка сгущения множества
- точка сгущения множества  . Тогда если
. Тогда если

и существуют пределы  и
и  , то
, то


 .
.
Теорема 5 (принцип двух милиционеров). Пусть функции  ,
,  и
и 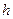 определены на множестве
определены на множестве  и
и  - точка сгущения множества
- точка сгущения множества  . Тогда если
. Тогда если
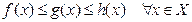
и существуют равные между собой пределы
 и
и 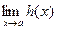 ,
,
то существует и равный им предел
 ,
,
т.е.

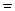

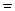
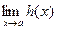 .
.
§2. Критерий Коши существования предела функции.
Теорема (критерий Коши). Пусть функция  определена на множестве
определена на множестве  и
и 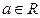 точка сгущения этого множества. Для того, чтобы существовал предел
точка сгущения этого множества. Для того, чтобы существовал предел

| (7)
|
необходимо и достаточно, чтобы 


 . .
| (8)
|
Д о к а з а т е л ь с т в о. Необходимость. Пусть существует предел (7) и для определенности пусть 
 . Выберем произвольное
. Выберем произвольное  . Тогда найдется такое
. Тогда найдется такое 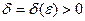 , что для любых
, что для любых 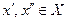 , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  и
и  справедливы неравенства
справедливы неравенства
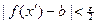 и
и  .
.
Поскольку  , то тогда при тех же
, то тогда при тех же 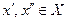 справедливо и неравенство (8). Необходимость доказана.
справедливо и неравенство (8). Необходимость доказана.
Достаточность. Покажем сначала, что для любой последовательности  , последовательность
, последовательность 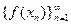 – фундаментальная и, следовательно, она имеет предел. Выберем произвольную последовательность
– фундаментальная и, следовательно, она имеет предел. Выберем произвольную последовательность  и произвольное
и произвольное  . По условию
. По условию  такое, что
такое, что  справедливо неравенство (8). Зафиксируем это
справедливо неравенство (8). Зафиксируем это 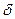 . Тогда в силу того, что
. Тогда в силу того, что 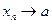 и
и  найдется такой номер
найдется такой номер  , что при
, что при 
 .
.
Таким образом,  при
при  , но тогда по выбору
, но тогда по выбору  имеем
имеем
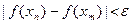 .
.
В силу произвольности выбранного  это и означает, что последовательность
это и означает, что последовательность 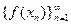 – фундаментальная.
– фундаментальная.
Покажем теперь, что для любой последовательности 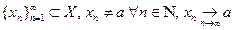 предел
предел  один и тот же. Тогда в силу определения предела функции по Гейне это и будет означать, что существует предел (7). Предположим противное, т.е. пусть имеются две последовательности
один и тот же. Тогда в силу определения предела функции по Гейне это и будет означать, что существует предел (7). Предположим противное, т.е. пусть имеются две последовательности 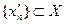 и
и  (
(  ), которые сходятся к точке
), которые сходятся к точке 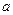 и
и 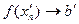 ,
,  , причем
, причем 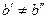 . Рассмотрим последовательность
. Рассмотрим последовательность
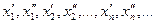 .
.
Очевидно, она сходится к точке 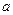 , при этом все ее точки принадлежат множеству
, при этом все ее точки принадлежат множеству  и отличны от точки
и отличны от точки 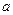 . Тогда по доказанному выше последовательность
. Тогда по доказанному выше последовательность

сходится и, следовательно, любые ее подпоследовательности имеют один и тот же предел, а это противоречит тому, что 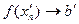 ,
,  и
и 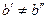 □
□
§ 2а. Локальные свойства функций, имеющих предел.
Определение 1. Пусть функция 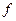 определена на множестве
определена на множестве  и
и 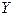 – некоторое его подмножество (
– некоторое его подмножество (  ). Говорят, что функция
). Говорят, что функция  ограничена на множестве
ограничена на множестве 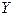 , если его образ
, если его образ  есть ограниченное множество.
есть ограниченное множество.
Замечание 1. Аналогично вводятся понятия ограниченности функции  на множестве
на множестве 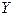 сверху и снизу.
сверху и снизу.
Замечание 2. Ограниченность функции  на множестве
на множестве  очевидно означает, что
очевидно означает, что 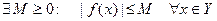 .
.
Теорема 1 (о локальной ограниченности). Пусть функция  определена на множестве
определена на множестве  и
и  - точка сгущения этого множества. Тогда если существует предел
- точка сгущения этого множества. Тогда если существует предел  , то в некоторой окрестности точки
, то в некоторой окрестности точки 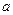 функция
функция  является ограниченной. Точнее, существует такая окрестность
является ограниченной. Точнее, существует такая окрестность 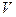 точки
точки  , что функция
, что функция  ограничена на множестве
ограничена на множестве 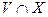 .
.
Д о к а з а т е л ь с т в о. Пусть  и
и  Тогда по определению предела для
Тогда по определению предела для  найдется такая окрестность
найдется такая окрестность  точки
точки  , что
, что

А так как
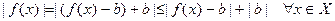 ,
,
то

Следовательно функция  ограничена на множестве
ограничена на множестве  , а тогда она, очевидно, ограничена и на множестве
, а тогда она, очевидно, ограничена и на множестве 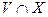 □
□
Ниже знак числа  обозначается через
обозначается через 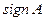 .
.
Теорема 2 (о стабилизации знака). Пусть функция  определена на множестве
определена на множестве  и
и  - точка сгущения этого множества. Тогда если существует отличный от нуля предел
- точка сгущения этого множества. Тогда если существует отличный от нуля предел  , то в некоторой проколотой окрестности точки
, то в некоторой проколотой окрестности точки  функция
функция 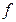 имеет тот же знак, что и этот предел: точнее, существует такая окрестность
имеет тот же знак, что и этот предел: точнее, существует такая окрестность 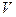 точки
точки  , что
, что
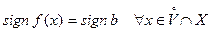
| (1)
|
Д о к а з а т е л ь с т в о. Пусть для определенности  .
.
Тогда  - некоторая окрестность точки
- некоторая окрестность точки 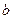 . По определению предела существует такая окрестность
. По определению предела существует такая окрестность 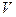 точки
точки 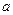 , что
, что  , а по выбору окрестности
, а по выбору окрестности 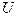 это означает, что
это означает, что  , и, следовательно, имеет место равенство (1) □
, и, следовательно, имеет место равенство (1) □
§ 2б. Предел суперпозиции.
Теорема (о пределе суперпозиции). Пусть функция 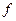 определена на множестве
определена на множестве  ,
, 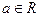 – точка сгущения множества
– точка сгущения множества  и существует предел
и существует предел
 . .
| (2)
|
Пусть, кроме того, функция  определена на множестве
определена на множестве 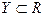 ,
, 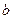 – точка сгущения множества
– точка сгущения множества 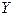 и существует предел.
и существует предел.
 . .
| (3)
|
Тогда, если 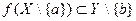 , то на множестве
, то на множестве  имеет смысл суперпозиция
имеет смысл суперпозиция  и существует предел.
и существует предел.
 . .
| (4)
|
Д о к а з а т е л ь с т в о. Выберем произвольную окрестность  точки
точки  . Тогда, в силу равенства (3), найдется окрестность
. Тогда, в силу равенства (3), найдется окрестность  точки
точки  такая, что
такая, что
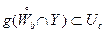
| (5)
|
В свою очередь, в силу равенства (2), для окрестности  точки
точки 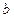 найдется такая окрестность
найдется такая окрестность  точки
точки  , что
, что
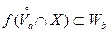 ,
,
а так как  и по условию
и по условию  , то отсюда следует, что
, то отсюда следует, что
 . .
| (6)
|
Из включений (5) и (6) следует, что
 .
.
Таким образом, для произвольно выбранной окрестности  точки
точки  нашлась окрестность
нашлась окрестность  точки
точки  такая, что
такая, что  . По определению предела это и означает, что имеет место равенство (4) □
. По определению предела это и означает, что имеет место равенство (4) □

