Понятие непрерывной функции
Определение 1. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любого
, если для любого  существует такое
существует такое  , что для любого
, что для любого  , удовлетворяющего неравенству
, удовлетворяющего неравенству
 , ,
| (1)
|
справедливо также и неравенство

| (2)
|
Замечание 1. Данное определение иногда называется определением непрерывности функции на языке  . По форме оно явно напоминает определение предела функции в форме Коши, при этом в отличие от него здесь требуется, чтобы точка
. По форме оно явно напоминает определение предела функции в форме Коши, при этом в отличие от него здесь требуется, чтобы точка  принадлежала множеству
принадлежала множеству  , но не требуется, чтобы она была точкой сгущения этого множества.
, но не требуется, чтобы она была точкой сгущения этого множества.
В связи с последним замечанием отметим, что если точка  не является точкой сгущения множества
не является точкой сгущения множества  , то она называется изолированной точкой этого множества. Иными словами точка
, то она называется изолированной точкой этого множества. Иными словами точка  называется изолированной точкой множества
называется изолированной точкой множества  , если существует такая ее окрестность
, если существует такая ее окрестность  , что
, что 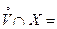 Æ или, что тоже самое,
Æ или, что тоже самое,  .
.
Замечание 2. Согласно определению 1 в любой изолированной точке своей области определения всякая функция является непрерывной. Действительно, каково бы ни было  по определению изолированной точки можно выбрать столь малое
по определению изолированной точки можно выбрать столь малое  , что
, что  и, следовательно, при этом
и, следовательно, при этом  среди точек множества
среди точек множества  неравенству (1) будет удовлетворять только точка
неравенству (1) будет удовлетворять только точка  , но для
, но для 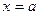 неравенство (2) очевидно выполняется для любой функции
неравенство (2) очевидно выполняется для любой функции  .
.
Замечание 3. В силу того, что для  неравенство (2) выполняется очевидным образом, можно заключить, что в том случае, когда точка
неравенство (2) выполняется очевидным образом, можно заключить, что в том случае, когда точка  является точкой сгущения множества
является точкой сгущения множества  , неравенство (1) можно заменить неравенствами:
, неравенство (1) можно заменить неравенствами:  , при этом определение 1 превратится в определение предела
, при этом определение 1 превратится в определение предела  при
при  . Таким образом, можно сказать, что если точка
. Таким образом, можно сказать, что если точка  является точкой сгущения множества
является точкой сгущения множества  , то функция
, то функция  будет непрерывной в этой точке в том и только том, случае, когда
будет непрерывной в этой точке в том и только том, случае, когда  .
.
Замечание 4. На языке окрестностей определение 1 можно переформулировать следующим образом:
Определение 1’. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любого
, если для любого  существует такое
существует такое  , что
, что
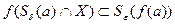
(т.е.  ).
).
Это определение, а значит и определение 1, очевидно равносильно следующему определению:
Определение 1”. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любой окрестности
, если для любой окрестности  точки
точки 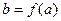 существует такая окрестность
существует такая окрестность  точки
точки  , что
, что
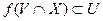 .
.
С учетом замечаний 2 и 3, теоремы о равносильности определений предела по Коши и по Гейне, а также с учетом того, что всякую точку  можно представить в виде
можно представить в виде 
 ,*) заключаем, что определения 1 и 1’ равносильны следующему определению:
,*) заключаем, что определения 1 и 1’ равносильны следующему определению:
Определение 2. Функция  ,
,  , называется непрерывной в точке
, называется непрерывной в точке  , если для любой последовательности точек
, если для любой последовательности точек  ,
,  , последовательность
, последовательность 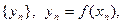 сходится и
сходится и
 .
.
Как будет показано далее все элементарные функции являются непрерывными в своих областях определения. В связи с этим напомним, что к числу, так называемых, основных элементарных функций относятся:
– постоянная функция: 
– степенная функция:  ;
;
– показательная функция:  ;
;
– логарифмическая функция: 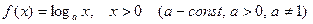 ;
;
– тригонометрические функции:
 ;
;
– обратные тригонометрические функции:
 .
.
В свою очередь, элементарной называется всякая функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических операций и образования суперпозиций.
Теорема 1 (О непрерывности сужения). Пусть функция  непрерывна в точке
непрерывна в точке  и
и 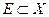 причем
причем  . Тогда функция
. Тогда функция  также непрерывна в точке
также непрерывна в точке  .
.
Д о к а з а т е л ь с т в о вытекает из определения сужения и определения непрерывности.
Теорема 2 (Арифметические свойства непрерывных функций). Пусть функции  и
и  определены на множестве
определены на множестве  и непрерывны в точке
и непрерывны в точке  . Тогда и функции:
. Тогда и функции:
 ,
, 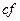
 ,
, 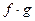 ,
, 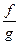 (при
(при  на
на  )
)
непрерывны в точке 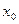 .
.
Теорема 3 (О локальной ограниченности). Пусть функция  определена на множестве
определена на множестве  и непрерывна в точке
и непрерывна в точке  . Тогда существует такая окрестность
. Тогда существует такая окрестность  точки
точки  , что функция
, что функция  ограничена на множестве
ограничена на множестве  .
.
Теорема 4 (О стабилизации знака). Пусть функция  определена на множестве
определена на множестве  и непрерывна в точке
и непрерывна в точке  . Тогда если
. Тогда если  , то существует такая окрестность
, то существует такая окрестность  точки
точки  , что
, что 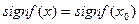
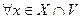 .
.
Наконец отметим еще две простые теоремы
Теорема 5. Пусть функция  определена на множестве
определена на множестве 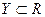 и непрерывна в точке, а функция
и непрерывна в точке, а функция  определена на множестве
определена на множестве  и непрерывна в точке
и непрерывна в точке  , причем
, причем  и
и  . Тогда сложная функция
. Тогда сложная функция  непрерывна в точке
непрерывна в точке 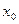 .
.
Д о к а з а т е л ь с т в о. Выберем произвольную последовательность  ,
,  . Так как
. Так как  - непрерывна в точке
- непрерывна в точке 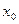 , то
, то
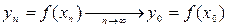 ,
,
а так как  , то
, то  . Поэтому, в силу непрерывности функции
. Поэтому, в силу непрерывности функции  в точке
в точке  , имеем
, имеем
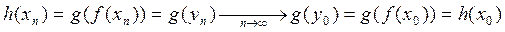 ,
,
то есть
 ,
,
что и означает, что функция  - непрерывна в точке
- непрерывна в точке 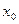 .
.
Пусть функция  определена на множестве
определена на множестве  и
и  . Рассмотрим множества:
. Рассмотрим множества:


Определение 1. Функция  называется непрерывной слева (непрерывной справа) в точке
называется непрерывной слева (непрерывной справа) в точке  , если функция
, если функция  (соответственно
(соответственно  ) непрерывна в точке
) непрерывна в точке  .
.
Замечание. На языке  определение, например, непрерывности слева, формулируется следующим образом: функция
определение, например, непрерывности слева, формулируется следующим образом: функция  называется непрерывной слева в точке
называется непрерывной слева в точке  , если
, если 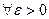
 такое, что
такое, что  удовлетворяющего неравенствам
удовлетворяющего неравенствам

справедливо неравенство
 .
.
Теорема 6. Функция  непрерывна в точке
непрерывна в точке 
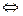 она непрерывна в ней слева и справа одновременно.
она непрерывна в ней слева и справа одновременно.
Если  - изолированная точка множества
- изолированная точка множества  , то утверждение очевидно. Если же
, то утверждение очевидно. Если же  - точка сгущения множества
- точка сгущения множества  , то оно вытекает из аналогичной теоремы об односторонних пределах.
, то оно вытекает из аналогичной теоремы об односторонних пределах.
§9. Точки разрыва функции. Классификация точек разрыва.
Определение 1. Пусть функция  определена на множестве
определена на множестве  и
и  . Если функция
. Если функция  непрерывна в точке
непрерывна в точке  , то она называется точкой непрерывности функции
, то она называется точкой непрерывности функции  . В противном случае, точка
. В противном случае, точка  называется точкой разрыва функции
называется точкой разрыва функции  .
.
Замечание 1. Так как всякая изолированная точка множества  является точкой непрерывности определенной на нем функции
является точкой непрерывности определенной на нем функции  , то точками разрыва могут быть только точки сгущения множества
, то точками разрыва могут быть только точки сгущения множества  .
.
Замечание 2. Если  – точка разрыва функции
– точка разрыва функции  , то либо предел
, то либо предел  не существует, либо он существует, но
не существует, либо он существует, но  .
.
Определение 2. Точка разрыва 1-го рода называется точкой устранимого разрыва функции  , если в ней существует предел функции
, если в ней существует предел функции  , но он не равен ее значению в этой точке.
, но он не равен ее значению в этой точке.
Замечание 4. Если точка  – точка устранимого разрыва функции
– точка устранимого разрыва функции  , то изменив ее значение в этой точке на значение, равное величине предела в этой точке, получим непрерывную функцию в этой точке
, то изменив ее значение в этой точке на значение, равное величине предела в этой точке, получим непрерывную функцию в этой точке
 .
.
Этим и объясняется термин точка устранимого разрыва.
В следующих двух определениях предполагается, что точка  принадлежит области определения функции
принадлежит области определения функции  вместе с некоторой своей окрестностью
вместе с некоторой своей окрестностью  .
.
Определение 3. Пусть  – точка разрыва функции
– точка разрыва функции  . Если оба односторонних предела
. Если оба односторонних предела  и
и  существуют и конечны, то она называется точкой разрыва 1-го рода
существуют и конечны, то она называется точкой разрыва 1-го рода
Определение 4. Точка разрыва функции называется точкой разрыва 2-го рода, если она не является точкой разрыва 1-го рода.
Замечание 3. Иными словами точка разрыва функции является точкой разрыва 2-го рода, если в ней хотя бы один из односторонних пределов не существует, либо является бесконечным.
Проиллюстрируем данные выше определения на некоторых примерах.
Пример 1 (всюду разрывной функции). Функция Дирихле, определенная на всей числовой оси равенствами:
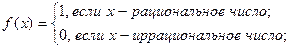
является разрывной в каждой точке  . Действительно, для любой последовательности рациональных чисел
. Действительно, для любой последовательности рациональных чисел  , сходящейся к точке
, сходящейся к точке  , имеем
, имеем  , а для любой последовательности иррациональных чисел
, а для любой последовательности иррациональных чисел 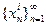 ,
,  , в свою очередь, имеем
, в свою очередь, имеем  . Следовательно, ни в одной точке
. Следовательно, ни в одной точке 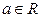 не существует предел
не существует предел  и, следовательно каждая точка
и, следовательно каждая точка  – точка разрыва функции Дирихле. Более того, нетрудно видеть, что ни в одной точке
– точка разрыва функции Дирихле. Более того, нетрудно видеть, что ни в одной точке  не существуют оба односторонних придела
не существуют оба односторонних придела  и
и  , так как описанные выше последовательности
, так как описанные выше последовательности  и
и  , с одной стороны, можно выбрать так, что
, с одной стороны, можно выбрать так, что  , а с другой стороны, можно выбрать и так, что
, а с другой стороны, можно выбрать и так, что  . Таким образом, каждая точка
. Таким образом, каждая точка 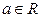 – точка разрыва 2-го рода функции Дирихле.
– точка разрыва 2-го рода функции Дирихле.
Пример 2. Функция «сигнум  »
»

очевидно, разрывна в точке  , причем эта точка – точка разрыва 1-го рода.
, причем эта точка – точка разрыва 1-го рода.
Пример 3. Функция  разрывна в точке
разрывна в точке  , которая, очевидно, является точкой устранимого разрыва.
, которая, очевидно, является точкой устранимого разрыва.

