|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
|
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ОСНОВЫ ТЕОРИИ КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ
4.1 Картографическа я проекция
Вформуле(3.11), обозначив (1+ 1)=kл -коэффициентла- Картографией называется область науки, техники и изводства, изучающая создание и использование картографи
(3.12) ких произведений. Картография подразделяется на математи кую картографию, картометрию, картоведение, проектирован составление карт, оформление и издание карт. Математическая картография разрабатывает вопросы мат тического обоснования карт и является первой ступенью в про Таким образом, коэффициентом лага называется число, на ко торое надо умножить разность отсчетов лага (рол), для того чтобы се создания карты. Картографируемая поверхность Земли имеет сложную кон получить пройденное судном относительное расстояние. В МТ-2000 для определения пройденного судном расстояния гурацию инеправильную геометрическую форму, а поэтому не жет быть описана математическими формулами. Для отображ помещена табл. 2.17, рассчитанная по формуле (3.11). ее на плоскости необходимо от физической поверхности Земли рейти к ее математической модели. Такая математическая мо будет весьма близка к физической поверхности, однако уже в жена математическими формулами. При картографировании за модель Земли принимают шар
50 Раздел 2. Картография ---------------------------------------- -- --
Картографической проекцией называется математически выра женный закон, связывающий географические координаты некото рой точки на поверхности криволинейной модели Земли с прямо угольными координатами этой же точки на плоскости. Общие уравнения картографических проекций имеют вид:
х =fi (< р, Л.),
у=! 2 (< р, Л.), Глава 4. Основы теории картографических проекций
 лишь в определенных точках или вдоль некоторых линий на к Точка карты (линия), в которой масштаб изображения равен ному масштабу, называется центральной точкой (центрально нией) проекции. В других точках карты масштаб изображени дет отличаться от главного. Поэтому, кроме главного масштаб различают еще и частный масштаб
где < р и л_-криволинейные географические координаты некоторой карте; dS - соответствующий ему бесконечно малый отрезо точки на картографируемой поверхности; х и у - прямоугольные координаты изображения этой же точки на плоскости в проекции, определяемой функциямиfi иf2. Свойства проекции будут зависеть от свойств и характера функ ций fi и f2. Поскольку этих функций может быть множество, то и получаемые проекции тоже могут быть разнообразными. Изображение семейства линий меридианов и параллелей на плоскости называется картографической сеткой. Каждой проекции соответствует определенная картографичес кая сетка, которая и составляет математическую основу создавае мых карт. картографируемой поверхности. Если главный масштаб характеризует общее уменьшение и ражения, то частный масштаб характеризует степень уменьш изображения только в данной точке карты. Отношение частного масштаба в данной точке по данном правлению к главному масштабу называется увеличением мас ба и характеризует степень искажения проекции или масштаб ты по отношению к условному глобусу:
С= 11/ llo = dsf ds 0 •
Увеличение масштаба изменяется при переходе от одной т карты к другой, а также по разным направлениям, проложеи 4.2 Масштаб
Карта должна быть не только плоским, но и уменьшен ным до необходимых размеров изображением поверхности. По этому, прежде чем проектировать на плоскость, картографируе мую поверхность уменьшают. Математическая модель Земли в за из одной и той же точки. Это приводит к искажению длин, нап лений, углов и площадей на проекции. Чем ближе увеличение масштаба к единице во всех точках ты, тем, следовательно, лучше и совершеннее выбранная для ной карты проекция. Разность между увеличением масштаба С и единицей наз данном масштабе, называется условным глобусом. Каждая карта имеет главный масштаб, который показывает об щую степень уменьшения всей картографируемой поверхности
ется относительным искажением длин или просто искаже
Если известны главный масштаб карты и ее частный масш данной точке, то искажение длин может быть подсчитано сра
- бесконечно малый отрезок тельно просто. Например, если главный масштаб llo = 1: 5000
конечно малый отрезок на картографируемой поверхности. После проектирования - развертки условного глобуса на плос кость - главный масштаб сохраняет свое численное значение частный масштаб ll = 1: 434 780, то увеличение масштаба С= 1 искажениедлин V= 0, 15 = +15%. Пусть на карте отрезок равен 50 мм, что при главном масш 1: 500000 соответствует расстоянию в 25000 м. Следовательно,
Глава 4. Основы теории картографических проекций
ствительное расстояние на местности, соответствующее данному отрезку карты, будет равно 25000: 1, 15 = 21739 м. Например, для карты масштаба 1: 500000 ПТМ = 0, 0002 х 5000 = 100м. На картах показывают только главный масштаб, который мо жет быть выражен в двух видах - числовом и линейном. Числовой масштаб изображается в виде дроби, числитель кото По сути, предельная точность масштаба равна тому миним ному расстоянию на местности, которое может быть изобра на карте. рой единица, а знаменатель показывает, какова степень уменьше Масштаб и предельная точность масштаба карты характериз ния длин на условном глобусе. Например; М= 1/10000 или М= разрешающую способность данной карты, а также определяют = 1/750000. Возможна и такая форма записи масштаба: М = 1: 100000 или м= 0, 000001. При графической работе на карте чаще используют линейный масштаб, показывающий число единиц, принятьrх для измерения длин на местности (км, мили), которое содержится в единице, принятой для измерения длин на карте (мм, см). Линейный мас штаб на специально вычерченной шкале показывает число кило метров, содержащихся в одном миллиметре или число миль в од пустимую погрешность, с которой на этой карте могут выполн ся графические построения.
4.3 Характеристик а искажени й проекции
Величины искажений являются одним из основньrх териев оценки достоинства карты. При картографировании и жения неизбежны, однако они подчиняются некоторым зак ном сантиметре. Иногда вместо построения шкалы ограничивают ся указанием: в 1 см - 1 кбт или в 1 см - 2 мили. На морских навигационных картах в проекции Меркатора ли мерностям и поэтому поддаются учету при работе на карте. П ную и наглядную характеристику искажений любой проекц любой ее точке дает эллипс искажений (индикатриса). Эллип нейный масштаб строят вдоль боковых рамок карты. На топогра кажений подобен изображению на карте бесконечно малой окр фических и географических картах линейный масштаб вычерчива ности на поверхности Земли с центром в этой точке. На земной ют под нижней рамкой карты в виде короткой шкалы. С уменьшением масштаба карты изображения небольших объ ектов становятся настолько малыми, что нанесение их на карту становится невозможным. Практикой установлено, что разрешаю верхности (рис. 4.1) показана окружность бесконечно малого диуса r 0 с центром в точке М 0. Отрезки меридиана и параллели ки М 0, ограниченные этой бесконечно малой окружностью, с ектированы на плоскость. щая способность невооруженного глаза человека равна О, 1 мм. По этому две точки, находящиеся на расстоянии менее 0, 1 мм одна от другой, усматриваются как одна. В соответствии с этим свойством зрения человека принято линейное расстояние на местности, со ответствующее на карте отрезку в О, 1 мм, называть предельной точ ностью масштаба (ПТМ). Кроме того, при составлении карты не избежны некоторые неточиости за счет погрешностей проектиро вания, вычерчивания контуров и погрешностей за деформацию бумаги. Поэтому при работе на карте уеловились считать, что пре дельная точность масштаба - это расстояние на местности, соот ветствующее отрезку на карте, равному 0, 2 мм. Предельная точность масштаба зависит от масштаба карты, вы ражается в метрах и рассчитывается следующим образом: В общем случае вследствие бесконечно малой их величины отрезки изобразятся прямыми линиями, но пересечение их на
где С- знаменатель главного масштаба карты.
Рис. 4.1. Окружность на земной поверхности (а) и эллипс искажений (б) на к
те в точке М обычно уже не образует прямого угла. Если на земной поверхности точка окружности Р 0 имеет прямоугольные коорди наты х 0 и у 0, то проекция этой точки Р на плоскости проекции (карте) имеет косоугольные координаты х и у. Обозначив масштаб вдоль меридиана т, а вдоль параллели n, согласно определению масштаба:
х Глава 4. Основы теории картографических проекций
а llmax = -; ro
• вдоль малой оси эллипса масштаб минимален т=-; Хо n=L. У о ь llmin =-. ro
Так как на земной поверхности бьmа показана окружность, то ее уравнение Считая r 0 =1, llmax =а, llmin = Ь. Эллипс искажений в данной точке данной проекции выра не только вектор максимального и минимального искажени
Хо Уо = ro · также общий характер и степень искажений по любому дру
С учетом выражений для т и n уравнение кривой, изображаю щей исходную окружность на карте в данном масштабе, будет иметь вид:
или направлению. Это его свойство позволяет оценивать основны рактеристики картографических проекций: масштабы площад масштабы длин 11, искажения углов ro.
4.4 Классификаци я картографически х проекций
В картографии проекции классифицируют по дву новным признакам: • по характеру искажений; • по виду меридианов и параллелей нормальной картограф кой сетки.
По характеру искажений различают равноугольные, равнов
Равноугольными проекциями называются проекции, не иска щие направлений и углов. В таких проекциях сохраняется под Полученное выражение является уравнением эллипса в сопря женных полудиаметрах. Из множества взаимно перпендикулярных диаметров исходной окружности всегда имеются два, которые в проекции изображают ся главными осями эллипса искажений. Направления этой пары называют главными направлениями. Во многих картографических проекциях главные направления не совпадают с меридианами и параллелями. Однако именно по этим направлениям значения фигур, масштаб зависит от положения точки на карте и не зав от направления, вследствие чего эллипсы искажений во всех ках карты будут превращаться в окружности различных ради Для этих проекций имеют место соотношения:
а= Ь, т= n, ro =О, р * 1.
На картах, сос1авленных в равноугольных проекциях, углы
ленги можно измерять и прокладывать непосредственно с помо
транспортира и протрактора. По сравнению с другими проекциями на них удобнее измерять расстояния. Благодаря этим особенносrям они широко применяются при составлении морских навигационных карт.
щади на картах пропорциональны площадям в натуре. В проекци ях эллипсы искажений имеют различную форму в различных мес тах карт, но площади их одинаковы. На картах в таких проекциях искажаются углы и нарушается подобие фигур. Для этих проекций справедливы соотношения: Глава 4. Основы теории картографических проекций
<
л
Рис. 4.2. Коническая проекция ---- =-о =- --
Для морских навигационных карт данный вид проекций не применяется. Равнопромежуточными называются проекции, в которых на картах в каждой точке сохраняются длины по одному из главных
В зависимости от ориентировки конуса относительно элли ида различают прямые, косые и поперечные конические пр ции. В прямой проекции ось конуса совпадает с земной осью, в направлений, т. е. в каждой точке или а= 1, или Ь = 1. Это неравен ство масштабов обусловливает искажение углов: перечной проекции - перпендикулярна земной оси, в косой - нимает промежуточное положение.
. 1-Ь . а-1 sшw=-- или sшw=--. 1+Ь а+1
Карты в таких проекциях в судовождении не применяются. Произвольными называются проекции, в которых не соблюдает ся ни одно из указанных свойств. Из их числа в судовождении на шла применение центральная перспективная проекция, известная Азимутальные проекции являются частным видом коничес проекций. Их уравнения имеют вид:
p=fiq> ); 8=Л.
Как следует из уравнений этих проекций, углы между мери нами на местности равны углам на проекции (рис. 4.3). под названием гномонической. В этой проекции дуга большого круга - ортодромия - изображается прямой линией. По виду меридианов и параллелей нормальной сетки различают конические, азимутальные, цилиндрические, перспективные и произвольвые (псевдоконические, псевдоцилиндрические, поли конические, круговые) проекции. Коническими называются такие проекции, в которых параллели изображаются концентрическими окружностями, а меридианы - радиальными прямыми линиями (рис. 4.2). В уравнениях этих проекций используют плоские полярные ко ординаты: Так же, как и конические, азимутальные проекции могут б прямыми, косыми и поперечными (рис. 4.4).
р =fiq> ); 8 =аЛ,
где р- радиус параллели на карте; 5- долгота на карте; а- коэф фициент пропорциональности (как правило, а < 1 ).
екция 58 Раздел 2. Картография Глава 4. Основы теории картографических проекций
А(< р, Л) 1 1
Рис. 4.4. Азимуrальная про- екция: а - поперечная; б - прямая; в- косая
го диаметра. Перспектинные проекции образуют самостоя ную группу азимутальных проекций, но их общие уравн идентичны.
Цилиндрическими называются проекции, на которых параллели В зависимости от удаления D точки зрения от центра услов глобуса, перспектинные проекции бывают (рис. 4.7): • центральные (гномонические), когда точка зрения находи центре условного глобуса (D = О); картографической сетки представляют собой прямые, параллель ные экватору, а меридианы- прямые, перпендикулярные парал лелям (рис. 4.5). Уравнения таких проекций имеют вид: • стереографические - точка зрения удалена от центра на ра условного глобуса (D = R); • внешние - точка зрения удалена на расстояние R < D < оо; • ортографические -точка зрения удалена в бесконечность ( D
где х, у - прямоугольные координаты точки на карте; < р, Л- геогра фические координаты этой точки; k - коэффициент пропорцио нальности. Так же, как и конические проекции, цилиндрические проекции могут быть прямыми, косыми и поперечными. Перспективными называют проекции земной поверхности - шара или эллипсоида - на касательную плоскость, получаемые прямым геометрическим проектированием из различных точек зрения (рис. 4.6). Все точки зрения лежат на диаметре условного глобуса, пер пендикулярном картинной плоскости или на продолжении это- Как и все остальные проекции, перспектинные проекции могут быть прямыми, косыми и поперечными. Для судовождения представляет особый интерес центра (гномоническая) проекция. Ее уравнения:
р = Rctg< p; 8 = Л; т = cosec2< p; n = cosec< p.
Неравенство масштабов по меридиану и по параллели оп ляет неравноугольность проекции. Однако эта проекция х терна тем, что на ней дуги больших кругов условного глобуса бражаются прямыми линиями (рис. 4.8). Иначе говоря, на ка этой проекции прямая линия, соединяющая две точки, явл также и кратчайшим расстоянием между ними. Это свойство
 Картинная плоскость х
А" ' А"
dx
А А' dy
02 02
Рис. 4. Z Виды перспек- Рис. 4.8. Центральная (гномоническая) проекция у в В' тивных проекций Рис. 5.1. К выводу уравнений цилиндрических проекций
в гномонической проекции используют при плавании по крат чайшим расстояниям для нанесения на меркаторские карты дуг больших кругов.
Глава 5 НОРМАЛЬНАЯ РАВНОУГОЛЬНАЯ ПРОЕКЦИЯ МЕРКАТОРА На плоскости проекция этой трапеции изобразится пр угольником АА'А" А" ' со сторонами dx и dy. Бесконечно малый отрезок меридиана
Ао'А 0 " = Rdq> - на шаре или Ао'А 0 " = Mdy на эллипсоиде. Бесконечно малый отрезок параллели
5.1
Общие формулы цилиндрических проекций
Уравнения меридианов и параллелей цилиндрических
АоАо' = rdA = Rcosq> dЛ - на шаре или
АоАо' = Ncosq> dA - на эллипсоиде, проекций в общем виде определяются выражениями
x=flq> ); y= а, (5.1)
где r- радиус параллели в широте q> (r = Rcosq> для шара, r = N для эллипсоида).
где С - коэффициент пропорциональности, определяющий рас стояния между меридианами. Отдельные цилиндрические проекции различаются между со
По определению масштаба
dx т=-; dX
n= dy. dY'
На рис. 5.1 показана бесконечно малая трапеция АоАо'А 0 " Ао" ', образованная на поверхности шара (или эллипсоида) пересечени ем бесконечно близких друг к другу меридианов и параллелей.
дляшара т = dx Rdr.p; dy dy n=-= ; rdJ... Rcosr.pdJ...
Глава 5. Нормальная равноугольная проекция Меркатора
для эллипсоида dx т=--· Md< p' n =-d y- = ---d-y'---
 rdЛ N cos < рdЛ б в
Для оценки искажения направлений ffi нужно знать полуоси а и Ь эллипса искажений. Так как в цилиндрических проекциях главные направления совпадают с меридианами и параллелями, то полуосям а и Ь соответствуют экстремальные масштабы т и n, поэтому
'Рз
Аз 'Рз
'Р2 а-Ь т-п sinffi=--=--. а+Ь т+п q q> 1
Таким образом, общими формулами для всех цилиндрических проекций будут: для эллипсоида: для шара:
х =.f{< p); у= 0.; х = J{< p); у= СА;
Рис. 5.2. Принцип построения меркатор а проекции
т=--· Rd< p' n= dy . Rcos< pdЛ' (5.3)
совместится с осью условного глобуса - признак нормаль (прямой) проекции. Меридианы условного глобуса спроектируем на боковую . а-Ь т-п SШ(J)=--=--. а+Ь т+п . а-Ь т-п Slllffi= -- = --. а+Ь т+п верхность цилиндра без искажения их длин (в натуральную ве чину), как бы выпрямляя их до полного совпадения с боковой верхностью цилиндра. Параллели жестко связаны с меридианами в точках их пере чения, поэтому при подобном проектировании каждая паралл ПрИIЩIШ построения меркаторской проекции будет растянута до размеров экватора. Чем больше широта пар лели, тем меньше ее длина и, следовательно, тем больше она р Картографическую проекцию для составления морских навигационных карт, отвечающую специфическим требованиям равноугольности и локсодромичности предложил в 1569 г. фла мандский картограф Герард Кремер (1512-1594), более известный под своим латинским псевдонимом- Меркатор. Именно в мерка торской проекции в наше время во всех странах издают практиче ски все морские навигационные карты, используемые для обеспе тянется при переносе ее на цилиндр. Степень растяжения парая лей пропорциональна sec < р и определяется выражением
R = rcos < р, (
где R - радиус экватора; r- радиус произвольной параллели; широта этой параллели. чения безопасности судовождения. Рассмотрим принцип построения меркаторской проекции. Примем Землю за шар, уменьшим его до необходимых размеров и далее будем рассматривать модель Земли как условный глобус, Если после такого проектирования развернуть цилиндр в пл кость, то получившаяся картографическая сетка будет иметь взаимно перпендикулярных прямых линий (рис. 5.2, б). Эква при проектировании на цилиндр не растягивался, поэтому э масштаб которого равен главному масштабу будущей карты. По ментарно малый круг, расположенный на нем в точке А 01 , изоб
сался поверхности цилиндра (рис. 5.2, а). При этом ось цилиндра зится точно таким же кругом и на карте- кругом А 1 • Произволь параллель < pi растянута (искажена), поэтому элементарно мал
круг Aoi' расположенный на этой параллели, изобразится на карте вытянутым вдоль параллели эллипсом А;. Чем больше широта < р, тем больше растяжение параллели и, следовательно, тем сильнее проявляется искажение круга при его переносе на плоскость. Это значит, что требование равноугольности не выполнено. Чтобы проекция обладала свойством равноугольности, необходимо ме ридианы в каждой точке вытянуть пропорционально растяжению параллели этой точки. Иначе говоря меридиан в широте < р; необхо димо удлинить настолько, чтобы эллипс А; превратился в круг А/ (рис. 5.2, в). Чем больше широта, тем сильнее растянута параллель и, следовательно, тем больше должен быть растянут меридиан. В результате одинаковые элементарно малые круги, расположенные на разных параллелях условного глобуса, изобразятся на карте кру гами разных размеров, увеличивающихся с широтой. Это свиде тельствует о том, что масштаб полученной карты изменяется про порционально широте, а точнее - пропорционально sec < р. По этой причине полученная картографическая сетка искажает длины. В частности, важно отметить, что и длина одной минуты меридиана (одна морская миля) на такой карте по линейной вели чине будет непостоянной, что усложняет работу штурманов по из мерению и прокладке расстояний. Если искажаются длины, то, зна чит, искажаются и площади. По этой причине остров Гренландия на Глава 5. Нормальная равноугольная проекция Меркатора
 q к р
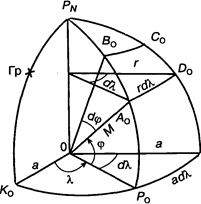
ал Рис. 5.3. К выводу уравнений меркаторской проекции
где < р, Л.- географические координаты точки на поверхности З ли; х, у- прямоугольные координаты этой же точки на карте; коэффициент пропорциональности, определяющий рассто между меридианами на карте. Для определения этого коэффициента примем Землю за эл карте в меркаторской проекции изображается по размерам пример соид вращения с большой полуосью а и рассмотрим на услов
но таким же, как и африканский материк, хотя в действительности площадь Африки почти в 15 раз больше площади Гренландии. Полученная таким образом проекция является прямой (ось ци глобусе произвольную точку Ао с координатами < р, Л. (рис. 5.3) карте она изобразится в виде точки А с прямоугольными коорд тамихиу. линдра совмещена с осью Земли), равноугольной (элементарно ма Предположим, что центральной линией проекции является лый круг на Земле изображается на карте также кругом), цилиндри ческой (меридианы и параллели являются взаимно перпендикуляр ными прямыми линиями). Прямоугольный вид нормальной карто графической сетки обусловливает прямолинейность локсодромии. ватор, который поэтому проектируется без искажений. Тогда Ко = КР. Но К 0 Р 0 = аЛ., а КР = у. Отсюда уравнение меридианов примет вид:
у= аЛ..
5.3 Уравнения проекции и их анализ
Для составления карты в меркаторской проекции необ ходимо знать математический закон построения карты. В общем виде этот закон для цилиндрических проекций в соответствии с Видно, что коэффициент пропорциональности равен боль полуоси (радиусу экватора) земного эллипсоида:
С= а. уравнениями (5.1) имеет следующее выражение: Для определения вида функции х = fi: < p) в условие равноуг
х=fi: < p); у= а, ности т = n следует подставить соответствующие выражения масштабов по меридиану и по параллели:
66 Раздел 2. Картография
dx dy Md Ncos d'A
Продифференцируем уравнение меридианов: dy = adA. Глава 5. Нормальная равноугольная проекция Меркатора
у= КЛ.
dx а Тогда--=-- Анализ уравнений проекции Меркатора позволяет сделать дующие выводы: Md Ncos • координатах не зависит от долготы Л. Следовательно, пост ному значению широты соответствует постоянное для вс Решение полученного дифференциального уравнения приво дит к табличному интегралу долгот значение х, т. е. параллели на карте представляют с семейство прямых линий, параллельных оси у; • координата у не зависит от широты < р. Следовательно, пос
х =а -sec oN
После подстановки значений радиусов кривизны земного эл липсоида М и N и интегрирования, получим уравнение параллелей ному значению долготы Л соответствует постоянное для широт значение у, т. е. меридианы на карте представляют с семейство прямых линий, параллельных оси х; • прямолинейность меридианов и параллелей подтверждает надлежиость меркаторской проекции к категории пр (нормальных);
n ]. • из прямолинейности и взаимной параллельности мериди следует, что локсодромия, пересекающая все меридианы одним и тем же углом, также является прямой линией; 2 1+еsш ) (5.5)
где е - эксцентриситет земного эллипсоида. Таким образом, уравнения меркаторской проекции, выражаю щие математический закон построения карты, имеют следующий вид: • параллельность меридианов и параллелей карты взаимно пендикулярным координатным линиям х и у является пр ком цилиндричности меркаторской проекции; • уравнение параллелей получено из условия равенства мас бов по меридиану и параллели, следовательно, проекция катора равноугольна.
Таким образом, анализ уравнений подтверждает, что мерк екая проекция удовлетворяет основным требованиям, предъ
n ]; емым к морской навигационной карте. Соблюдение этих усл 2 1+еsш ) на картах в меркаторской проекции позволяет прокладыва них без искажений углы и направления, измеренные на местн а линию пути судна, идущего постоянным курсом (локсодром у= аЛ. прокладывать прямой линией при помощи обычной линейки
С помощью этих уравнений географические координаты точки и Л преобразовываются в прямоугольные картографические ко Кроме того, равноугольность проекции обусловливает под форм (контуров) объектов в натуре и на карте. Это в значител степени способствует опознанию местности по ее изображ (форме) на карте, и наоборот. Поэтому меркаторскую прое
центриситет е= О. Следовательно, относят к конформным проекциям - проекциям, сохраняю подобие форм.
Ортодромия на земной поверхности пересекает меридианы под разными углами, отличающимися друг от друга на угол схождения
Так как q> 2 > q> 1, то cosq> 2 < cosq> 1 , и, соответственно, cosq> 1 1cos > 1, а это означает, что всегда n2 > n 1. меридианов. На карте в проекции Меркатора меридианы- парал лельные прямые. Следовательно, ортодромия, пересекал парал лельные меридианы под разными углами, изобразится на карте кривой линией. То есть прокладка дуги большого круга (ортодро мии) на картах в меркаторской проекции усложнена, что затрудня Таким образом, при изменении широты характер измен масштаба следующий: • с увеличением широты масштаб увеличивается; • с уменьшением широты масштаб уменьшается. ет плавание по кратчайшим расстояниям. Меркаторекая проекция имеет и другие недостатки, с которы ми мореплавателям приходится мириться: • проекция не сохраняет равенство площадей; • невозможно создание меркаторской карты для приполюсных С учетом сжатия Земли изменение масштаба с широтой б характеризоваться
где N1 и N2 - радиусы кривизны сечения по первому вертикал • масштаб на картах в меркаторской проекции изменяется с ши ротой, что вносит искажения в измеренные циркулем расстоя параллелях q> 1 Если в и q> 2 .
х (5.8) и (5.9) перейти к знаменателям чи ния даже в пределах одного листа карты.
5.4 Изменение масштаба. выражения вых масштабов С1 и С2, то получим: для Земли-шара с1 с2 = cosq> 1fcosq> 2; ( |
Последнее изменение этой страницы: 2019-05-04; Просмотров: 365; Нарушение авторского права страницы
эллипсоид вращения, малая ось которого совпадает с осью вра ния Земли. Эти фигуры нельзя развернуть на плоскости, поэт при создании карт используют различные способы проектир ния. При этом основная задача математической картографии стоит в том, чтобы спроектировать на плоскость систему геогр ческих координат - сетк-у параллелей и меридианов.
52 Раздел 2. Картография
ПТМ = 0, 0002 С, 
54 Раздел 2. Картография
• вдоль большой оси эллипса масштаб максимален
масштабов экстремальны: 
Равновеликими или равноплощадными называются проекции, на которых масштаб площадей во всех точках карты одинаков и пло
х
х 
местим условный глобус в цилиндр так, чтобы по экватору он ка
64 Раздел 2. Картография
х = R ln tg (45° + }
68 Раздел 2. Картография