Процентные точки критерия Романовского

α	nцр
	4	6	8	10	12	15	20	30	40	50	100
0, 01	6, 530	4, 355	3, 712	3.408	3, 233	3, 074	2, 932	2, 802	2, 742	2, 707	2, 640
0, 05	3, 558	2, 777	2, 508	2, 291	2, 215	2, 145	2, 079	2, 079	2, 048	2, 030	1, 994
0, 10	2, 631	2, 177	2, 010	1, 923	1, 869	1, 819	1, 772	1, 727	1, 706	1, 693	1, 669

 

Критерий Романовского позволяет при приведении статистических данных к выбранному закону распределения устранить некоторые экспериментальные результаты, признав их промахами.

Выбор меры расхождения, вычисляемой по формуле (3.9), не является единственно возможным. Л. Н. Колмогоров в качестве меры расхождения между теоретическим и экспериментальным распределениями предложил использовать максимальное значение модуля разности между теоретической и эмпирической функциями распределения:

Рис. 2.7. К определению критерия А. Н. Колмогорова

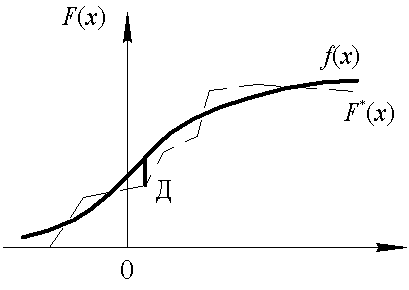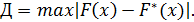
Применение этого критерия на практике сводится к следующему:

1. На одном графике строят статистическую и теоретическую функции распределения (рис. 2.7).

2. Определяют максимальное значение разности между ними.

3. Находят величину

(n – число наблюдений над случайной величиной).

4. По полученному значению l, пользуясь табл. 3.14, находят значение вероятности р(l). Это есть вероятность того, что за счет случайных причин расхождение между функциями F*(x) и F(x) будет не меньше, чем полученное по результатам данной серии испытаний. При малых значениях р(l) гипотеза отбрасывается, при больших значениях р(l) гипотеза принимается.

Таблица 3.14

Числовые параметры функции F ( x )

l	P(l)	l	P(l)	l	P(l)
0, 0 0, 1 0, 2 0, 3 0, 4 0, 5 0, 6	1, 000 1, 000 1, 000 1, 000 0, 997 0, 964 0, 864	0, 7 0, 8 0, 9 1, 0 1, 1 1, 2 1, 3	0, 711 0, 544 0, 393 0, 270 0, 178 0, 112 0, 068	1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0	0, 040 0, 022 0, 012 0, 006 0, 003 0, 002 0, 001

 

Критерий А. Н. Колмогорова удобно применять на практике вследствие его простоты и наглядности. Однако следует помнить, что применение его дает достоверные результаты в том случае, если заранее известны числовые параметры, характеризующие функцию F(x).

 

Контрольные вопросы

1. В чем заключается основная задача расчетов на надежность?

2. Какие методы расчетов надежности используют на практике?

3. Какие основные допущения принимаются при использовании приближенных методов расчета надежности? Как эти допущения влияют на точность расчетов?

4. Расскажите о сущности коэффициентных методов расчета надежности.

5. Как определяются точечные и интервальные показатели надежности?

6. Объясните основные этапы экспериментальных методов определения надежности.

7. Какие методы проверки статистических гипотез используются при оценке параметров надежности?

8. Дайте классификацию видов испытаний авиационного оборудования на надежность.

 

Глава 4

ПОТОКИ ОТКАЗОВ

 

Приборы и системы авиационной аппаратурыв случае отказа подлежат ремонтуили заменеисправными.Для восстановленного изделия с момента окончания ремонтанаработка системыдалее продолжает возрастать.Особенно это касаетсямеханических деталей и узлов, в которых происходит изнашивание, старение материалов, развитие дефектов. Все это приводит к возникновению нового отказа и очередному восстановлению. В целом возникают потоки отказов и восстановлений.После ремонта изделия егоустановка предусматривает последующее испытание и ввод в эксплуатацию с оформлением соответствующих документов. Однако когда-то появляется отказ, после которого изделие не подлежит ремонту и заменяется новым (исправным и сертифицированным). В том и другом случае, основной целью является восстановление функционирования системы, в которую входило отказавшее изделие.

Вопросы ремонта могут рассматриваться с позиции системы массового обслуживания (СМО). Рассмотрим систему, состоящую из n работающих приборов и rканалов обслуживания. Отказ прибора в случайный момент времени порождает заявку на обслуживание, а поток отказов порождает соответственно поток заявок. При свободных каналах заявки обслуживаются немедленно, а если все r каналов заняты, заявки выстраиваются в очередь. Для системы с ожиданием выполняется условие , где k – число отказов приборов.

Для простейшего потока заявок (отказов) и обслуживания представим основные параметры:

λ – интенсивность поступления заявок (отказов) от одного прибора (полагаем λ = const);    

Λ = n ∙ λ – суммарная интенсивность заявок системы из n однородных приборов;

μ – интенсивность обслуживания (восстановления, ремонта, замены) в одном канале;

r∙ μ – суммарная интенсивность обслуживания во всех r каналах.

Для эксплуатанта замена отказавших изделий новыми, сертифицированными является более предпочтительной, чем ремонт, поскольку сокращает время простоя. Это предпочтительно и для ремонтного предприятия, появляется возможность ликвидировать простои в случае временного отсутствия заявок, выполняя восстановление и испытание полученных ранее отказавших изделий с последующей консервацией и складированием.

 

Параметр потока отказов

Процессы функционирования восстанавливаемых изделий можно представить схематически (рис. 3.1). Здесь каждая горизонтальная линия 1... N изображает процесс наработки и восстановлений отдельного изделия. Крестиками показаны моменты отказов и восстановлений изделий. По абсциссе откладываются только времена наработки изделий, а времена восстановлений не учитываются.

 

х

t

Δ t

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

х

tл

t1

0

2

4

6

8

10

N

t

Рис. 4.1. Схема восстанавливаемых процессов функционирования

с деградирующими изделиями

 

Наличие нескольких крестиков означает соответственно и несколько отказов - восстановлений одного и того же изделия. Если крестик стоит в конце линии наработки, это обозначает появление отказа, после которого изделие заменяется новым.

Для этого нового изделия отсчет наработки начинается от оси ординат. Например, после отказа изделия 3 оно заменено изделием 4, а отказавшее изделие 6 заменено изделием 7. Соответственно такому процессу замен в совокупности изделия имеют различные наработки. То изделие, которое имеет максимальную наработку, в дальнейшем будет называться лидирующим. На рисунке лидирующим является изделие 2.

Эту схему, в которой ведется учет наработки каждого из изделий, а восстанавливается только отказавший элемент в изделии, будем называть первой схемой функционирования восстанавливаемых изделий или схемой функционирования с деградирующими изделиями, или деградирующей схемой функционирования изделий. При такой схеме изделие в целом стареет в процессе работы, хотя в нем могут появляться и отдельные новые элементы.

В качестве показателя надежности для восстанавливаемых изделий используется не интенсивность отказов, а параметр потока отказов.

Параметр потока отказов есть математическое ожидание числа отказов, приходящееся на один час суммарной наработки большого (стремящегося к бесконечности) числа изделий в момент t.

Для каждого интервала, примыкающего к моменту наработки процесса функционированияt, статистическое значение параметра потока отказов определяется зависимостью:

 

где общее число отказов во всем парке испытуемых изделий на достаточно малом интервале времени Δ t, примыкающем к t; – суммарная наработка всех N изделий на интервале Δ t.

Пример 4.1. Рассматривается работа 50 изделий, проработавших период времени t = 500 часов. На интервале времени  часов, примыкающем к моменту времениt = 500 часов, отказало, и было восстановлено 5 изделий. Определить параметр потока отказов на интервале

Решение. Суммарная наработка изделий на интервале ч. (Время восстановления не учитываем):

 

 

Параметр потока отказов

 

При N → ∞ и Δ t → 0 из (4.1) получается аналитическое значение параметра потока отказов:

 

Внешне формула (4.1) совпадаетс выражением для интенсивности отказовневосстанавливаемых изделий

 

но в данном случаев в входят только первые отказы изделий, а в (4.1) – все отказы, включая первые, вторые и т. д. для каждого из учитываемых изделий. Кроме того, в (4.1) количество изделий, вступивших в эксплуатацию, остается неизменным. При возникновении отказа отказавшее изделие либо ремонтируется, либо заменяется на исправное.  

Для интенсивности и плотности вероятности отказов невосстанавливаемых изделий существуют различные математические зависимости. Даже " классическая" кривая f(t) (рис. 4.2) может быть описана суперпозицией двух законов распределения.

Однако для рассматриваемой первой схемы функционирования восстанавливаемых изделий подобные математические зависимости пока отсутствуют. В основном это связано со сложностью сбора статистики по вторым, третьим и т.д. отказам для различных изделий. Поэтому на практике приходится пока использовать только статистические значения параметра потока отказов. При наличии таких данных можно судить об общем уровне надежности изделия, о скорости изменения этого уровня.

 

f(t)

f(t)

t

I

II

III

Рис. 4.2. График зависимости плотности вероятности отказа изделия

 

Можно рассчитать вероятность безотказной работы изделия на достаточно малом интервале времени, например, за время Δ t полета самолета. Для такого интервала, примыкающего к моменту t₁наработки изделия (рис. 4.1), среднее значение параметра потока отказов можно принять . Тогда вероятность отсутствия отказа в полете

 

 

Для рассматриваемых восстанавливаемых изделий характеристикой надежности является также средняя наработка на отказ. Она является обратной функцией параметра потока отказов:

 

 

В пределе средняя наработка на отказ есть суммарная наработка большого числа (стремящегося к бесконечности) изделий на малом (стремящемся к нулю) интервале времени, приходящаяся на один отказ на этом интервале:

 

  Эта характеристика, как и для невосстанавливаемых изделий, является функцией наработки . Она реально существует для каждой точки оси времени, ее не следует смешивать (что иногда делают) со средней наработкой на отказ изделий за интервал времени эксплуатации от 0 до

гдеt _j, п _j –наработка ичисло отказов j-го изделия за времяэксплуатации от 0 доt; t – текущее время эксплуатации; N–число изделий.

Значение (4.6) получается тем точнее, чем больше N.

Однако данное утверждение справедливо только для случая схемы функционирования с деградирующими изделиями. Более сложной оказывается задача получения достаточно строгой математической зависимости параметра потока отказов для схемы с восстанавливаемыми деградирующими изделиями. Научные исследования, опирающиеся на реальный статистический материал, могутспособствовать повышению надежности авиационной техники.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться: