Графическое представление цветов в системе RGB

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒

Как мы уже знаем, любой цвет однозначно характеризуется тремя цветовыми координатами–количествами основных цветов системы RGB: Ц®{R, G, B}. Другими словами, цвет является вектором в некотором трехмерном пространстве. Естественно считать, что все цветовые векторы имеют общее начало, которое соответствует «нулевому количеству цвета» – чёрному цвету.

Рисунок 52 – графическое представление цвета в системе RGB

Направим векторы основных цветов произвольным образом, но так, чтобы они не лежали в одной плоскости: Цветовые векторы складываются по обычным правилам, следовательно:

§ Если цвет Ц описывается положительными количествами основных цветов, то его цветовой вектор будет лежать внутри треугольной пирамиды, построенных на векторах . Если одна из координат вектора будет отрицательна, то вектор расположится вне пирамиды.

§ Так как при аддитивном сложении цветов никогда не образуется чёрный цвет, то не существует цветовых векторов с диаметрально противоположными направлениями. Поэтому всевозможные цветовые вектора заполняют не всё пространство, а лишь некоторую его часть.

§ Рассмотрим треугольник Δ RGB, полученный при соединении концов векторов основных цветов - так называемы «треугольник единичных цветов». Концы векторов, соответствующих всевозможным единичными цветами [Ц] (цветам, для которых модуль цвета m равен единице) будут лежать в плоскости π, содержащей данный треугольник. Действительно, уравнение для координат точки, принадлежащей плоскости π и уравнение для координат вектора единичного цвета совпадают: r+q+b =1

Координаты {R, G, B} векторов Ц, соответствующих различным спектрально-чистым цветам были экспериментально определены Райтом и Гилдом. По известным координатам можно построить эти вектора, и тем самым нанести на плоскость π точки всех существующим в природе чистых цветов – получить так называемый «цветовой график»:

Цветность произвольной смеси монохроматических излучений всегда изображается точкой {r, g, b}, лежащей внутри фигуры, ограниченной замкнутой линией BFGRB. Поэтому данная фигура называется «поле реальных цветов».

Рисунок 53 - Цветовой график системы RGB

Точкой Е на рисунке обозначен равноинтенсивный белый цвет. Введем еще несколько определений:

Линия, на которой расположены точки цветности всех монохроматических излучений называется линия спектральных цветов или спектральный локус.

Линия, соединяющая точки цветности основного красного и основного синего цветов (т. R и т. B) называется линия пурпурных цветов, на ней расположены максимально насыщенные пурпурные цвета.

Отметим две важные особенности цветового графика:

1. Цветов с отрицательным значением координаты b (закрашенная область « b < 0 » на рисунке 9.4) очень мало, поэтому в большинстве практических расчетов можно считать, что для этих цветов b=0.

2. Цветов с отрицательным значением координаты r (закрашенная область « r < 0 » на рисунке 9.4) очень много: они располагаются вне Δ RGB, на площади ограниченной отрезком BG и кривой BFG.

Указанный недостаток снижает точность вычислений и не может быть устранен выбором вместо RGB другой триады основных цветов, так как не один треугольник с вершинами в точках, соответствующих реальным цветам, не охватывает спектральный локус (смотри, например, Δ RFB).

Система описание цветов XYZ (1931г)

Для упрощения цветовых расчётов, а значит повышения их точности, было крайне желательно избавиться от отрицательных значений координат. Система RGB и все ее аналоги, основанные на триадах спектральных цветов, не смогли обеспечить выполнения такого требования. Поэтому МКО была разработана цветовая система XYZ, в которой реальные цвета были заменены тремя не воспроизводимыми (чисто формальными) цветами, условно названными « Х », « Y » и « Z ».

Цвета X, Y и Z лежат вне поля реальных цветов. Они выбраны так, чтобы Δ XYZ полностью охватывал спектральный локус, а расчёты яркости для реальных цветов были наиболее простыми:

1.6

Рисунок 54 Цветовой график системы RGB, с нанесенными основными цветами системы XYZ

Координаты основных цветов системы XYZ (записанные в системе RGB):

(Х) ® {r = 1.2750. g = – 0.2778, b = 0.0028}
(Y) ® {r = – 1.7393, g = 2.7673, b = – 0.0280}
(Z) ® {r = – 0.7431, g = 0.1409, b = 022}

Алихна («бесcветная») – геометрическое место точек нулевой яркости.

Из рисунка 54 следует, что основные цвета «Х» и «Z» лежат на алихне, поэтому они не дают вклада в яркость цвета – для вычисления яркости достаточно знать только количество цвета Y.

Единичные количества для основных цветов данной системы выбрали таким образом, чтобы в сумме основные цвета давали белый цвет Е, причём точно такой же, как и при сложении цветов [R], [G] и [В]. Данный подход называется «согласование с белым цветом Е»:

[Х] + [Y] + [Z] = [R] + [G] + [B] = Е (9.12)

Итак, в качестве основных цветов системы XYZ, были выбраны следующие цвета:

[Х] ® {r= 2, 36461, g= – 0.51515, b= 0.00526} - « ЦВЕТ X »

[Y] ® {r= – 0.89654, g= 1, 42640. b= – 0.01441} - « ЦВЕТ Y »

[Z] ® {r= – 0.46807, g= 0.08875, b= 1, 00921} - « ЦВЕТ Z »

§ Цветовое уравнение в системе XYZ

В системе XYZ цветовое уравнение имеет тот же вид, что и в системе RGB:

Ц=X× [X] + Y× [Y]+ Z× [Z], (9.13)

где X, Y и Z – количества основных цветов [X], [Y] и [Z] соответственно

Еще раз напомним, что согласно принципу построения рассматриваемой цветовой системы, количества цветов, входящие в уравнение (9.13), есть строго положительные величины.

§ Модуль цвета (m) и координаты цветности {x, y, z} рассчитываются стандартным способом:

m = X+Y+Z, (9.14)

(9.15)

Единственное отличие системы ХYZ от системы RGB состоит в том, что координаты цветности в системе XYZ нельзя измерить непосредственно в эксперименте, их выражают через ранее найденные координаты {r, g, b} по формулам:

, (9.16) где

A = (0.66700× r + 1.13239× g + 1.20058× b) (9.17)

Отметим, что если формулах (9.16) опустить коэффициент «А» (положить Аº 1), то все записанные выражения останутся справедливыми, только они будут относится уже не к переводу координат цветности {r, g, b}®{x, y, z}, а к пересчету цветовых координат из одной системы в другую {R, G, B}®{X, Y, Z}.

§ Получим выражение для световогопотока в системе XYZ:

(1) Используем факт согласования систем RGB и XYZ с единичным белым цветом Е:

Система RGB ® Ф_Е= 1·Ф_R + 1·Ф_G + 1·Ф_В (А)

Система XYZ [2] ® Ф_Е= 1·Ф_X + 1·Ф_Y + 1·Ф_Z = Ф_Y (Б)

Приравняв выражения (А) и (Б), находим Ф_Y:

Ф_Y = Ф_R+Ф_G₊Ф_В»1.00 лм + 4.59 лм + 0.06 лм=5.65 лм

Точное значение: Ф_Y =5.6508 лм

(2) Зная Ф_Y, выражаем световой поток в системе XYZ:

Ф_[Ц]= Y·Ф_y =5.6508·Y (9.18)

Записанная формула позволяет по известным координатам {X, Y, Z} определить световой поток для заданного цвета. Для единичных цветов в формулу (9.18) вместо « Y » необходимо подставлять « у ». Так как точное знание количества некоторого цвета (то есть точное знание светового потока) не влияет на его качественные характеристики, иногда множитель «5.6508» опускают. В этом случае полагают

Ф_[Ц]= Y (9.19)

Величина «Ф_[Ц]» носит уже относительный характер. Естественно, так же относительный характер будет носить и вычисленная по этому световому потоку яркость В. Чтобы отличить яркость, вычисленную по упрощенной формуле (9.19), от полученной по точной формуле (9.18), «яркость по упрощенной формуле» еще называют « относительная яркость».

§ Удельные координаты для монохроматических излучений (кривые сложения) в системе XYZ

Величины в системе XYZ получают расчётным путём. Последовательность действий – совершенно аналогична вычислениям в системе RGB[3]. Имеем:

(9.20)

Обратите внимание на важную особенностью формул (9.20) – удельная координата . Этот факт упрощает расчёты и позволяет произвести независимую проверку.Результаты вычислений изображены на рисунке 9.7. Видно, что удельные координаты для всех излучений в системе XYZ всегда положительные!

Рисунок 51 –удельные координаты цвета для всех спектрально-чистых цветов в системе CMYK. Мощность: 1/683 Вт

Данный график показывает, в каких количествах необходимо смешать основные цвета системы XYZ (с учетом единичных количеств), чтобы воспроизвести цвет монохроматического излучения с длиной волны λ и мощностью 5.6508 / 683 Вт

Рисунок 51 иллюстрируетудельные координаты спектральных цветов с различной длиной волны (в системе XYZ)

Точно так же, как и в системе RGB, общий множитель в формулах (9.20) – в данном случае это «683 / 5.6508» – при вычислениях часто опускают: он не важен для расчета качественных характеристик цвета. Чтобы понять, опущен ли множитель или нет для конкретных кривых сложения, достаточно посмотреть на кривую : если максимальное значение равно единице, значит множитель опущен. Пользуясь данным простым критерием, мы легко заключаем, чтопри построении графика 52 общий множитель действительно был опущен.

Цветовой график системы XYZ

Рисунок 52 - Цветовой график системы XYZ

Точка Е - равноинтенсивный (равностимульный ) белый цвет. Точки А и В - некоторые цвета.

§ Преобладающая длина волны (λ _d) на цветовом графике системы XYZ

Чтобы определить преобладающую длину волныλ _dдля некоторого заданного цвета А, необходимо из точки Е через точку цвета провести луч до пересечения с границей поля реальных цветов. Для нахождения длины волны дополнительного цвета λ _с, луч проводят в противоположную сторону, так же до пересечения с границей поля реальных цветов.

Отметим важные особенности пурпурных цветов:

(1) Если точка λ _с принадлежит линии пурпурных цветов, то для такого цвета дополнительного не существует

(2) Пурпурные цвета являются сложными (представляют собой смесью красных и фиолетовых цветов), поэтому их характеризуют особым образом. Для нахождения λ _d луч направляют не к линии пурпурных цветов, а в противоположную сторону, в сторону спектрального локуса. При этом, рядом с найденным числом ставится знак « ^/» или «–». Например, для точки В: «λ _d = – 506 нм» или «λ _d ^/= 506 нм».

§ Колориметрическая чистота (P_К) на цветовом графике системы XYZ

Колориметрическая чистота некоторого цвета А (см. рисунок 9.7) определяется его удаленностью от точке белого цвета Е: чем точка А ближе к точке Е, тем чистота меньше, и наоборот, чем точка А ближе к спектральному локусу, тем чистота больше. По известным координатами цветности {x, y}, колориметрическая чистота вычисляется следующим образом:

или

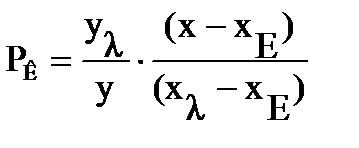- через координаты «х» (9.21)

- через координаты «y», (9.22)

где x_l и y_l - координаты спектрально - чистого цвета «λ _d» того же тона, что и данный цвет (точка «преобладающей длины волны» для данного цвета»), для пурпурных цветов x_λ и y_λ берутся на линии пурпурных цветов;

Рисунок 53 – колориметрическая чистота некоторого цвета А

x_Еи y_Е- координаты точки Е (так называемого « опорного белого цвета »),
обычно полагают x_Е≈ y_Е≈ 1/3.

Итак, формула (9.21) или (9.22) позволяет выразить колориметрическую чистоту через координаты цветности. Для удобства вычислений, на цветовом графике обычно нанесены так называемые «линии равной условной чистоты» (другое название: «линии равной условной насыщенности »).

Условная насыщенность Р_В вводится по формулам:

или

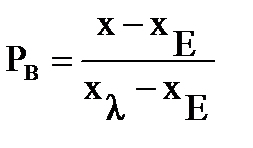- через координаты «х» (9.23)

- через координаты «y» (9.24)

На рисунке 53Цветовой график системы XYZ с нанесенными линиями условной насыщенности

Сравнивая формулы для колориметрической чистоты (9.21) и (9.22) с формулами (9.23) и (9.24) для условной чистоты, получаем:

(9.25)

Рассмотрим два крайних случая использования формулы (9.25):

Для цветов, расположенных вблизи точки Е: Р_в≈ 0 Þ Р_K ≈ 0.

Для цветов вблизи локуса: Р_в ≈ 100%, y_l/y ~1 Þ Р_K ≈ 100%

Нетрудно заметить, что в приведенных примерах Р_K ≈ Р_в. Таким образом, для цветов с малой и с большой условной чистотой Р_в колориметрическую чистоту цвета Р_K можно приближено прировнять условной чистоте цвета.

§ Аддитивное сложение двух цветов на цветовом графике системы XYZ

Цвет аддитивной смеси двух излучений Ц лежит на отрезке, соединяющем точки смешиваемых цветов. Точка Ц разделяет отрезок Ц₁Ц₂на две части, длины которых обратно пропорциональны модулям смешиваемых цветов:

Рисунок 54 - Аддитивное сложение двух цветов на цветовом графике системы XYZ

«Первый цвет» Ц₁ → цветовой модуль «m_1»

«Второй цвет» Ц₂ → цветовой модуль «m₂»

Ц = Ц₁+Ц₂– суммарный цвет:

m = m₁+m₂,

Таким образом, чтобы получить цвет, обозначенный на цветовом графике точкой А, необходимо смешать спектрально-чистый цвет того же тона «l_d» и белый цвет «Е» в соотношении:

Нахождение результата аддитивного смешивания двух цветов (в системе XYZ) (рисунок 54)

Отметим, что результат сложения нескольких цветов может быть найден и чисто аналитически, без использования цветового графика. Действительно, согласно свойствам цветовых векторов:

(9.26)

где X₁, Y₁, Z₁- цветовые координаты первого из складываемых цветов (Ц₁),
X₂, Y₂, Z₂- цветовые координаты второго из складываемых цветов (Ц₂),
X, Y, Z - цветовые координаты суммарного цвета (Ц= Ц₁+Ц₂).

В нашем случае цвета заданы по-другому, своими координатами цветности: Ц₁®{x₁, y₁}, Ц₂®{x₂, y₂}. Поэтому перед тем как воспользоваться формулами (9.26), необходимо вычислить цветовые координаты {X_i, Y_i, Z_i } для каждого из складываемых цветов, основываясь на знаниях об их «количестве».

Для простоты, предположим, что количества складываемых цветов заданы посредствам указания из цветовых модулей: Ц₁® m₁, Ц₂®m₂. Используя последовательно формулы (9.15) и (9.26) получаем:

(9.27)

где {x, y} - искомые координаты цветности суммарного цвета Ц.

4.3 Основы количественной колориметрии. Цветовой график МКО

Количественно оценивать любой цвет можно, исходя из явления смешения цветов. Все существующие цвета могут быть получены путем смешения трех взаимно независимых цветов — красного, зеленого и синего, взятых в определенных количествах. Эти основные цвета обозначают начальными буквами английских названий таких цветов:

R — красный (red), G — зеленый (green), В — синий (blue).

Световые потоки при смешивании образуют белый цвет (при определенной яркости и длинах волн R, G и B).

C количественной точки зрения основные независимые цвета являются единичными.

Рисунок 55 – Гипсовая призма с полями сравнения

(простейший измерительный прибор)

Поля сравнения цветности и яркости — грани условной

белой призмы, освещенные монохроматическим цветным

излучением — Ц и тремя взаимно независимыми излучениями красного — R, зеленого — G и синего — B цветов

На рис. 55 показана гипсовая призма, грани которой условно названы полями сравнения (это простейший светоизмерительный прибор).

Одно из полей, освещенное каким-либо хроматическим цветом, обозначим буквой Ц, а второе — тремя основными цветами R, G, B.

Белый гипс неизбирательно отражает белый свет, поэтому первое поле сравнения будет иметь такой же цвет, как и освещающий его светопоток Ц, и будет иметь яркость, определяемую величиной светового потока, отраженного от этого поля сравнения.

Второе поле сравнения, освещенное цветами R, G, B, должно быть неотличимо от первого как по цветности (цветовой тон и чистота цвета), так и по яркости.

Условие тождественности обоих полей сравнения математически выражается формулой (см. рис 55, а):

(1)

Оба поля имеют одинаковую цветность и яркость, значит, и световые потоки, освещающие их, равны по величине и цветности.

Формула (1) — это цветовое уравнение, которое показывает, что для получения цвета, тождественного с цветом Ц, надо смешать

r' единиц красного цвета R, g' единиц зеленого цвета G' и b' единиц синего цвета B. Таким образом, r', g' и b' — это коэффициенты цветового уравнения, показывающие, сколько единиц каждого из основных цветов надо взять, чтобы получить данный цвет Ц. Эти коэффициенты называют координатами цвета (r', g', b' ). Произведения r'R, g'G, b'B являются составляющими цвета Ц и называются цветовыми составляющими.

Опыты смешения цветов показывают, что для целого ряда цветов Ц для получения равенства обоих полей сравнения по цветности и яркости к цвету Ц, освещающему одно из полей сравнения, необходимо добавить еще некоторое количество одного из основных цветов (см.рис. 55, б).

Например, для одного из таких цветов Ц цветовое уравнение будет иметь вид:

(2)

Для каждого из таких цветов Ц тождественность полей сравнения получается только при одном определенном соотношении между r', g', b', причем к одним из цветов Ц для получения цветового равенства полей сравнения необходимо прибавить определенное количество цвета R, к другим — цвета G, к третьим — цвета B.

Перенесем цветовую составляющую g'G (2) в правую часть

тождества:

(3)

При такой форме записи цветового уравнения одной из цветовых составляющих условно приписывается отрицательное значение.

Основные цвета R, G, B в принятой системе определения цветов являются постоянными, поэтому заданный цвет Ц определяется полностью (по цветности и яркости) координатами цвета r', g', b', являющимися переменными величинами.

Во многих случаях практика требует лишь качественной характеристики цвета излучения источника света или светового потока, отраженного от поверхности предмета. В этом случае удобно пользоваться относительными значениями координат цвета, являющимися отношением каждой из координат цвета r', g' и b' к их сумме r'+g'+b'.

Относительные значения координат цвета носят название координат цветности и обозначаются r, g, b:

(4)

(5)

Итак, качественная характеристика цвета (цветность) определяется тремя координатами цветности r, g, b, в сумме равными единице.

Исходя из этого любой цвет может быть изображен графически.

Как известно, алгебраическая сумма, т. е. с учетом знака (рис. 56) перпендикуляров, опущенных из любой точки, находящейся внутри или вне равностороннего треугольника, на его стороны, равна его высоте.

Возьмем высоту равностороннего треугольника, равную единице. Тогда сумма перпендикуляров, опущенных из любой точки внутри или вне его на его стороны, будет равна единице. Поскольку сумма координат цветности также равна единице, то каждый из перпендикуляров, опущенных из точки внутри (вне) равностороннего треугольника на его стороны, может представлять одну из координат цветности (см. рис. 53).

Рисунок 56 – Графическое изображение представления цвета с помощью треугольной модели

Изображение цвета с помощью цветового треугольника, в вершинах которого расположены основные цвета R, G, B

Исходя из этого любой цвет может быть изображен точкой внутри (или вне) равностороннего треугольника, имеющего высоту, равную единице.

В вершинах такого цветового треугольника расположены основные цвета R, G, B.

Все цвета, которые могут быть получены непосредственным смешением трех основных цветов R, G, B в соответствии с уравнением (1) размещаются внутри цветового треугольника), (рис. а). Перпендикуляры, опущенные из точки Ц, которая изображена внутри треугольника, на его стороны, равны соответствующим координатам цветности и в сумме — единице.

Перпендикуляр, опущенный на сторону, лежащую против той вершины треугольника, где расположен цвет R, дает координату цветности r. Остальные перпендикуляры, опущенные на стороны треугольника, расположенные против вершин, в которых находятся цвета G и В, дают координаты цветности g и b. В этом случае все три координаты цветности r, g и b — п о л о ж и т е л ь н ы.

Те цвета, которые не могут быть получены непосредственным смешением цветов R, G и B, располагаются вне цветового треугольника (см. рис. 3, б). В этом случае перпендикуляры, опущенные из точки цвета Ц на стороны треугольника, также равны соответствующим координатам цветности и в сумме — единице.

Однако, в отличие от варианта а), в варианте б) одна из координат цветности (-r) о т р и ц а т е л ь н а. Этот случай соответствует уравнению (3).

В первой трехцветной международной колориметрической системе определения цветов RGB, построенной по изложенным выше принципам, в качестве основных цветов были взяты следующие величины монохроматических излучений:

— R (красный) — 700 нм,

— G (зеленый) — 546, 1 нм,

— B (синий) — 435, 8 нм.

Красный цвет был получен с помощью лампы накаливания и красного светофильтра, зеленый и синий цвета — путем выделения излучений с длинами волн 546, 1 и 435, 8 нм из спектра излучений ртутной лампы.

Трехцветной колориметрической системой была названа такая система определения цвета, которая основана на возможности воспроизведения данного цвета путем аддитивного смешения трех основных цветов R, G, и B.

Световые потоки единичных основных цветов R, G, и B подобраны так, чтобы при их смешении в центре равностороннего цветового треугольника получался белый цвет.

На сторонах цветового треугольника располагаются цвета, получающиеся в результате смешения цветов R, G, и B, находящихся в вершинах треугольника. На биссектрисах треугольника располагаются цвета, получающиеся при смешении каждого из основных цветов с белым цветом, находящимся в центре. Для того чтобы нанести на цветовой треугольник положение всех остальных спектральных цветов, необходимо знать значение цветности (координат цветности r, g, и b) для всех спектральных цветов. Эти значения были в свое время получены в результате лабораторных исследований, которые заключались в уравнивании цвета двух полей сравнения при освещении одного из них последовательно спектральными монохроматическими излучениями всей видимой области спектра через интервал 5 нм, а второго — комбинациями основных цветов R, G, и B.

На рис. 57 показан цветовой треугольник с линией спектральных цветов по данным этих исследований. Цифрами вдоль линии спектральных цветов указаны длины волн (в нм) соответствующих спектральных цветов.

Рисунок 57 – цветовой треугольник с линией спектральных цветов

Все спектральные цвета, кроме основных R, G, и B, расположены здесь вне цветового треугольника, и, следовательно, для каждого из них одна из координат цвета является отрицательной.

Такой график носит название цветового графика. На линии, соединяющей красный цвет с длиной волны 700 нм и фиолетовый цвет с длиной волны 400 нм, расположены неспектральные, чистые пурпурные, цвета.

Таким образом, цветности всех цветов располагаются на цветовом графике на площади, ограниченной кривой спектральных цветов (в форме вытянутого языка) и прямой линией пурпурных цветов. Зная координаты цветности r', g' и b' какого-либо цвета (излучаемого или отражаемого), можно рассчитать координаты цвета [см. формулу (4)] и нанести цвет Ц1 на цветовой график.

На прямой линии, соединяющей белый цвет Е (в геометрическом центре треугольника BGR) с цветом Ц1 и продолженной до линии спектральных цветов, будут расположены цвета, получаемые при смешении в разных пропорциях спектрального цвета (с цветовым тоном λ 1) и белого цвета Е. Одним из таких цветов и является цвет Ц1. Все цвета, расположенные на прямой линии λ 1E, имеют одинаковый цветовой тон λ 1, но отличаются друг от друга по чистоте (насыщенности) цвета, т. е. по степени разбавленности белым цветом.

На линии спектральных цветов насыщенность цветового тона равна 100 %.

Для цвета Ц1 чистота цвета больше 0 и меньше 100 %. Любой цвет, имеющий чистоту менее 100 % (т. е. не являющийся спектральным), может быть получен смешением какого угодно множества пар цветов. Цвета, расположенные на кривой спектральных цветов, являются 100 %-ми насыщенными цветами спектра (красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый) и смесями соседних цветов между собой. Пурпурные чистые цвета также определяются как 100 %-е насыщенные.

Все плюсы рассмотренной цветовой системы (в виде цветового графика), ее наглядность, доступность не исключают, однако, основного ее недостатка — наличия в ней отрицательных координат цветности, что значительно усложняет цветовые расчеты. Геометрически это обусловлено тем, что цветовой треугольник, построенный на основе цветов R, G и B, неизбежно оказывается внутри линии спектральных и пурпурных цветов.

Не представляется возможным построить цветовую систему, в которой отсутствовали бы отрицательные координаты цветности, путем применения в качестве основных цветов любых монохроматическихизлучений [3].

Недостатки такой системы определения цветов давно заставили ученых в области колориметрии работать над созданием более совершенной системы, свободной от отрицательных координат цветности.

И в 1931 г. Международная комиссия по освещению (МКО) приняла и утвердила новую колориметрическую систему определения цвета — XYZ. Эта система, как и предыдущая, построена на основе трех основных цветов, условно названных X, Y и Z и являющихся в этой системе единичными. Вся область существующих цветов заключена здесь в н у т р и прямоугольного треугольника, в вершинах которого расположены основные цвета X, Y и Z. Цветовой график в этой системе помещается таким образом, что все координаты цветности для существующих цветов оказываются положительными. Выражение основных цветов X, Y и Z через цвета R, G и B осуществляется путем ряда математических преобразований. Единицам X, Y и Z не следует придавать здесь никакого иного смысла, кроме расчетного. Выражения для X, Y и Z получаются путем преобразования уравнений в колориметрической системе RGB. Цветовое уравнение описывает процесс смешения цветов. Любой существующий цвет Ц выражается в системе XYZ следующим образом:

Рисунок 58 - Расположение основных цветов X, Y и Z на цветовом графике системы RGB

Здесь, как и в системе RGB, x', y', z' являются координатами цвета.

Координаты цветности X, Y и Z выражаются через координаты цвета:

(7)

(8)

На основании значений координат цветности r, g и b были вычислены координаты цветности в колориметрической системе XYZ для всех спектральных цветов [3].

Независимыми, как следует из равенства X + Y + Z = 1, являются только две из трех координат цветности.

Цветовой график в системе XYZ получается на основе откладывания по оси ординат одной из координат цветности, а по оси абсцисс — другой из них для всех спектральных и наиболее чистых пурпурных цветов.

В колориметрической системе XYZ общепринятым является цветовой график, по оси ординат которого откладываются координаты цветности Y (вертикальная ось), а по оси абсцисс — координаты цветности X (горизонтальная ось).

Поскольку X + Y + Z = 1, то, зная координаты цветности X и Y, можно получить значение третьей координаты цветности Z путем вычитания из единицы суммы значения координат X и Y. Поэтому в этом графике можно обходиться лишь двумя координатами X и Y, что упрощает расчеты и схему самого графика.

Таким образом, стандартный график МКО XYZ представляет собой прямоугольную координатную сетку с осями X и Y прямоугольного треугольника (который сам по себе чаще всего и не показан на графике). Прямоугольная сетка представляет собой часть поля этого прямоугольника. Сетка по осям ординат и абсцисс через одно деление (может быть меньше или больше) имеет обозначения членений осей Y и X как десятых долей единицы.

В нижнем левом углу, где пересекаются (сходятся) оси Y и Х, — нулевое значение шкал отсчета, далее по оси ординат Y идут (через 1 квадрат) членения от 0, 1 до 0, 8, а по оси абсцисс Х — членения от 0, 1 до 0, 7.

На поле координатной сетки нанесена знакомая нам кривая линия спектральных цветов(напоминающая язык), замыкаемая в основании (под углом к оси Х) прямой линией пурпурных цветов. Попериметру контура цветового графика нанесены значения цветовых тонов (в нм) в следующей последовательности: фиолетовый —в левом нижнем углу, над ним — синий, голубой, зеленый (за вершиной графика справа), желто-зеленый, желтый, оранжевый, красный.

А на прямом нижнем участке — условные значения длин волн ряда пурпурных цветов (со знаком ' : 500'–560' ) от красного до фиолетового. В верхней части графика, где происходит переход от голубого к зеленому и от зеленого к желто-зеленому, он растянут (интервалы между значениями цветовых тонов больше). В левой и правой его частях, ближе к основанию, график сжат (значения цветовых тонов очень близко расположены друг к другу).

В середине поля графика расположена точка белого цвета Е. На прямых линиях, соединяющих белый цвет (Е) со спектральными цветами (на кривой линии) и с пурпурными цветами (на прямой линии), располагаются цвета ненасыщенные, получающиеся от смешения спектральных или пурпурных цветов с белым [3].

График МКО (как и цветовые круги) не дает картины смешения спектральных и пурпурных цветов с черным и серыми различной светлоты. Это присуще двухмерным цветовым моделям. В этом их недостаток. Полноту картины смешения всех цветов (хроматических с ахроматическими) дают лишь трехмерные модели (см. тему 5).

Рисунок 59 - Цветовой график МКО. Для определения доминирующей длины

волны (нм) спектральных цветов или дополнительной длины волны пурпурных цветов вдоль линии спектральных цветностей указаны длины волн

монохроматического цвета.

В качестве точки отсчета используется точка цветности для стандартного излучения (А, В, С, D 65 МКО) или для равноэнергетического света (Е). На графике точка С — цветность излучения С МКО (дневной свет); точка Р — цветность пигмента кадмия красного (длина волны 605 нм). Чистота цвета — частное от деления отрезка СР на всю длину линии (до точки 605)

На рис. П.1.14 показан график МКО 1931 г. Точка С (внутри его поля) обозначает цветность излучения и подразумевает спектральный состав дневного рассеянного солнечного света. Новые стандарты излучений, разработанные МКО позднее, ввели, помимо С — дневного света, дополнительные обозначения:

— А МКО — свет лампы накаливания с вольфрамовой нитью, мощностью 500 Вт;

— В МКО — дневной свет — прямой солнечный свет (его спектральный состав).

Дальнейшие уточнения привели к появлению обозначений D МКО — это различные фазы дневного света: D55, D65 (спектральный состав типичного дневного света в диапазоне 300–830 нм), D75. На координатной сетке графика МКО обозначения могут располагаться в разных местах, на соответствующем расстоянии от точки Е — равноэнергетического света (смешение всех спектральных цветов — белый цвет).

Таким образом, в современных графиках МКО, являющихся наглядным и удобным графическим средством исследований в области колориметрии и определения (расчета) цветов, в качестве точки отсчета используются точки цветности для различных фаз дневного света (рассеянного), прямого солнечного света и искусственного света (лампы накаливания 500 Вт), обозначаемые, как указано выше, буквами — A, B, C, D55, D65, D75.

Это позволяет рассчитывать изменения того или иного цвета (как чистого насыщенного, так и смешанного, разбеленного) в зависимости от различного естественного или искусственного освещения [1], [3].

Лекция 5. Системы цветов в компьютерной графике

· Цветовая модель RGB

· Цветовая модель CMYK

· Цветовая модель HSB

· Цветовая модель HSL

· Цветовая модель CIE Lab

· Индексированные цвета

· Преобразование цветовых моделей

5.1 Понятие цветовой модели

Мир, окружающий человека, воспринимается по большей части цветным. Цвет имеет не только информационную, но и эмоциональную составляющую. Человеческий глаз — очень тонкий инструмент, но, к сожалению, восприятие цвета субъективно. Очень трудно передать другому человеку свое ощущение цвета.

Вместе с тем для многих отраслей производства, в том числе для полиграфии и компьютерных технологий, необходимы более объективные способы описания и обработки цвета.

Для описания цвета придуманы различные цветовые модели. Наиболее используемые делятся на три больших класса: аппаратно-зависимые (описывающие цвет применительно к конкретному устройству цветовоспроизведения, например, монитору, — RGB, CMYK), аппаратно-независимые (для однозначного описания информации о цвете — XYZ, Lab) и психологические (основывающиеся на особенностях человеческого восприятия — HSB, HSV, HSL) (рис. 60).

Рисунок 60 - Иерархия цветовых моделей

В графических редакторах для присвоения цветовых параметров объектам можно использовать несколько цветовых моделей в зависимости от задачи. Эти модели различаются по принципам описания единого цветового пространства, существующего в объективном мире.

5.2 Цветовая модель RGB.

Множество цветов видны оттого, что объекты, их иизлучающие, светятся.

⇐ Предыдущая 1 2 345 Следующая ⇒