Зависимость фазовой и групповой скоростей от частоты

⇐ ПредыдущаяСтр 4 из 9Следующая ⇒

Характеристическим сопротивлением направляемой волны называют отношение поперечных (к направлению ) составляющих вектора и вектора . Можно показать [13.1], что для -волны характеристическое сопротивление равно

(13.3.11)

где 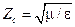– характеристическое сопротивление свободной волны, а для -волны оно равно

(13.3.12)

Как видим, характеристические сопротивления -волны и -волны зависят от частоты (длины волны). В режиме переноса энергии ( ) всегда меньше и при приближении к слева стремится к нулю (рис. 13.3.2); в закритическом режиме ( ) чисто мнимое. Наоборот, в режиме переноса энергии всегда больше и при приближении к слева стремится к бесконечности; в закритическом режиме чисто мнимое.

Характеристические сопротивления для Е-волны и Н-волны

При рассмотрении формул (13.3.4), (13.3.5), (13.3.6), (13.3.8), (13.3.9) может показаться, что величины одинаковы для -волн, -волн и гибридных волн. Однако, это неверно: величины , зависят от поперечного волнового числа , которое, в свою очередь зависит от формы и размеров поперечного сечения ЛП и от вида направляемой волны; остальные величины зависят от . Таким образом, все перечисленные величины зависят от формы и размеров поперечного сечения ЛП и вида волны.

Поперечные волны

В сравнении с рассмотренными выше волнами, имеющими продольные составляющие, поперечные -волны устроены намного проще. Полагая в (13.2.7) , получаем для -волны:

(13.4.1)

или в векторном виде, справедливом для произвольной системы координат в поперечном сечении ЛП:

(13.4.2)

Эта однородная система уравнений имеет нетривиальные решения только при . С учетом этого из (13.3.4), (13.3.5) следует, что для -волны . В свою очередь, это означает, что если в направляющей системе может распространяться -волна, то эта возможность имеется на всех частотах (длинах волн), включая , т. е. на постоянном токе. Отсюда следует, что -волна может распространяться только в направляющих системах не менее чем второго порядка связности; например, она не может распространяться в волноводах любого сечения (связность первого порядка) или в диэлектрических ЛП (связность нулевого порядка).

В уравнения (13.2.8) не входит частота, значит функции поперечных координат не зависят от частоты и могут быть найдены на основе решения рассматриваемой задачи при . Отсюда следует важный квазистатический принцип, позволяющий упростить решение задачи: для определения векторов достаточно решить двумерные электростатическую и магнитостатическую задачи для той же линии.

Предостережем читателя от слишком буквального понимания квазистатического принципа: во-первых, статическая аналогия относится только к распределению поля в поперечном сечении линии, распределение вдоль оси в корне отличается от постоянного и носит волновой характер; во-вторых, аналогия позволяет найти комплексные амплитуды электрического и магнитного полей, полные поля включают еще фактор , задающий колебания во времени, отсутствующие в статических полях.

Подставляя в (13.3.6), (13.3.8), (13.3.9) условие ( 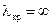), и в (13.2.7) – условия , обнаруживаем, что для -волны коэффициент фазы , фазовая скорость , длина волны в линии и характеристическое сопротивление равны:

,	(13.4.3)
,	(13.4.4)

(13.4.5)

(13.4.6)

т. е. в направляемой -волне эти параметры те же самые, что в свободной волне, распространяющейся в безграничной однородной изотропной среде без потерь с теми же параметрами , что в диэлектрике линии.

Выше предполагалось, что проводимость металлических частей ЛП идеальна. Если это условие не выполняется, электромагнитное поле проникает в металл, появляется продольная составляющая вектора и существование -волны невозможно. Однако при высокой проводимости металла структура поля волны мало отличается от структуры -волны и этим отличием пренебрегают. Это же замечание относится и к волнам с продольной составляющей вектора и (или) вектора : отличие структуры реальных волн при реальной высокой проводимости металла от рассмотренной выше структуры настолько мало, что им обычно пренебрегают.

Электрическая прочность ЛП

Средняя по периоду мощность, переносимая волной по ЛП, равна интегралу по поперечному сечению от действительной части продольной составляющей вектора Умова-Пойнтинга [13.1]:

(13.5.1)

где – максимальное значение напряженности электрического поля в ЛП;

– безразмерная векторная комплекснозначная функция, зависящая только от поперечных координат и определяющая структуру электрического поля в поперечном сечении ЛП;

– поперечная составляющая комплексного вектора , введенного в (13.2.3);

– характеристическое сопротивление распространяющейся волны:

для волн соответственно.

Как следует из (13.5.1), увеличение средней по периоду передаваемой мощности связано с увеличением максимальной напряженности электрического поля . Это, в свою очередь, приближает к предельному значению , при котором происходит электрический пробой воздуха или диэлектрического заполнения ЛП, характеризующийся большими токами и резким уменьшением активного сопротивления в разрядном промежутке, большим выделением тепла и резким повышением температуры в месте пробоя. Поступление мощности в нагрузку практически прекращается, а большая часть энергии падающей волны отражается от места пробоя и может вывести из строя генератор и вызвать другие нежелательные явления. Таким образом, электрический пробой в ЛП недопустим.

С другой стороны, увеличение приводит к возрастанию мощности потерь в металлических элементах линии и заполняющем диэлектрике, т. е. их нагреву, что приближает материалы к разрушению и так называемому тепловому пробою. Предельной мощностью называется меньшая из мощностей, вызывающих электрический или тепловой пробой. Для электрического пробоя это мощность, определяемая предельной напряженностью поля , равной при нормальных давлении воздуха и ионизации примерно 30 кВ/см; для теплового пробоя определяют по температуре, при которой возникает тепловое разрушение материалов, образующих линию. Появление отраженных волн в реальной линии может привести к электрическому или тепловому пробою при мощности, существенно меньшей, чем . Поэтому допустимую мощность принимают в несколько раз меньшей, чем предельная, например, .

Затухание в ЛП

Выше анализ свойств направляемых волн для простоты проводился в предположении, что ЛП не вносит потерь. Зависимость векторов поля от координаты задавалась множителем , где в режиме переноса энергии – действительное положительное и имеет смысл коэффициента фазы, а в закритическом режиме – мнимое положительное, обусловливая быстрое затухание волны, не отвечающей условию распространения . В реальной ЛП и в режиме переноса энергии волна ослабевает по мере движения вдоль линии, или затухает. Затухание волны связано, во-первых, с поглощением части передаваемой мощности в металлических частях линии, во-вторых, с поглощением в заполняющем диэлектрике, в-третьих, с излучением части мощности в окружающее пространство (в ЛП открытого типа). Поэтому в реальной ЛП в режиме переноса энергии зависимость векторов поля волны от описывается множителем

(13.6.1)

где

(13.6.2)

– постоянная распространения, комплексная величина, ее действительная часть – коэффициент ослабления, имеющий размерность 1/м. Теперь зависимость амплитуды вектора поля от описывается произведением двух экспонент:

(13.6.3)

первая из которых задает затухание амплитуды с логарифмическим декрементом , а вторая – отставание по фазе. Поскольку мощность пропорциональна квадрату амплитуды, затухание по мощности задается множителем .

Можно показать [13.1], что коэффициент ослабления, обусловленный потерями в металлических элементах ЛП, равен:

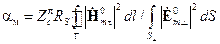(13.6.4)

где – активная часть поверхностного сопротивления проводника;

Гн/м, – удельная проводимость материала стенки волновода;

– касательная составляющая вектора ;

– контур поперечного сечения металлических элементов ЛП (односвязный в случае полого металлического волновода, двусвязный из двух концентрических окружностей – в случае коаксиальной линии и т. д.).

Прямоугольный волновод (Е-волны, Н-волны, основная волна, одноволновая передача, затухание)

Будем считать, что стенки волновода имеют бесконечную проводимость, а заполняющая его среда – идеальный (без потерь) диэлектрик с параметрами . Поскольку эта направляющая система имеет порядок связности 1, в ней могут существовать -волны и -волны, но не -волны (см. 13.4 ). На рис. 13.7.1 показаны применяемые далее система координат и размеры широкой и узкой стенок ( ). Источники, создающие поле в волноводе, расположены со стороны отрицательных значений координаты , а созданные ими волны распространяются в положительном направлении оси .

⇐ Предыдущая 1 2 345 6 7 8 9 Следующая ⇒