Пучности и узлы в ЛП в режиме смешанных волн

⇐ ПредыдущаяСтр 9 из 9

3) При интерференция падающей и отраженной волн образует стоячую волну, в которой максимумы называют пучностями, а минимумы – узлами (рис. 14.9.1). Степень глубины стоячей волны определяется лишь величиной : при =1 глубина максимальна, в пучности относительная амплитуда равна 2, в узле – равна 0 (такую картину иногда называют чисто стоячей волной); при 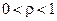пучность ниже двух, а узел выше нуля; при стоячей волны нет: отраженная волна отсутствует, относительные амплитуды напряжения и тока при всех равны 1, имеет место режим бегущей волны.

4) Фазовый угол влияет лишь на координаты узлов и пучностей, но не на значения амплитуды в них.

5) Как видно из рис. 14.9.1, минимум амплитуды вблизи узла выражен более резко, чем максимум амплитуды вблизи пучности. Это свойство стоячей волны важно в измерениях с помощью длинных линий: измерение положения пучности менее чувствительно, чем положения узла, зато проводится при большем «отношении сигнал-шум».

6) Для исчерпывающего описания распределения амплитуд вдоль линии достаточно изучить поведение напряжения по (14.9.1), поскольку распределение тока (14.9.2) повторяет распределение напряжения, но со смещением вдоль линии на .

7) Для количественного описания глубины стоячей волны вводят коэффициент стоячей волны, равный отношению максимальной и минимальной амплитуд:

(14.9.3)

откуда

(14.9.4)

Коэффициент стоячей волны – скалярная величина, принимающая значения в диапазоне

(14.9.5)

Левая граница этого диапазона соответствует полному согласованию, , т. е. режиму бегущей волны, правая – полному рассогласованию, , т. е. режиму чисто стоячей волны. И тот, и другой режимы на практике не достижимы в полной мере и являются математической абстракцией, приближение к которой возможно в той или иной степени. Идеально согласованная нагрузка невозможна из-за тепловых потерь, различных нерегулярностей и неоднородностей, обусловленных конечной точностью изготовления линии, наличием элементов крепления, несовершенством разъемов и других факторов, вызывающих появление отраженной волны. Идеальная полностью отражающая нагрузка невозможна из-за паразитных емкости, индуктивности и утечек.

Режимы работы ЛП без потерь

Обычно режимы в нагруженной ЛП разделяют на три класса:

1) Режим бегущей волны: линия согласована, , , отраженная волна отсутствует, распространяется только падающая волна, которая полностью поглощается нагрузкой, амплитуды напряжения и тока постоянны вдоль линии.

2) Режим чисто стоячей волны: , в сечении амплитуда отраженной волны равна амплитуде падающей волны, энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор, , .

3) Режим смешанных волн: 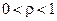, , часть энергии падающей волны поглощается нагрузкой, остальная ее часть в виде отраженной волны возвращается обратно в генератор, стоячая волна имеет неполную глубину, т. е. в пучности относительная глубина меньше двух, в узле относительная глубина больше нуля.

Канонические нагрузки

Рассмотрим распределения вдоль линии без потерь амплитуд напряжения и тока и входного сопротивления для нагрузок: согласованной резистивной нагрузки, холостого хода, короткого замыкания, емкости, индуктивности [14.6]. Эти нагрузки можно назвать каноническими; примеры, связанные с ними, помогают лучше понять структуру волн в нагруженной линии, а также имеют самостоятельный интерес.

Согласованная нагрузка

Далее считаем волновое сопротивление чисто активным , тогда согласованная нагрузка – сопротивление, равное волновому ( ). Как указано выше, при такой нагрузке получается режим бегущей волны с постоянными вдоль линии амплитудами напряжения и тока и линейной фазой (рис. 14.11.1). Напряжение и ток в этом режиме (см. (14.5.10)) равны:

(14.11.1)

поэтому

(14.11.2)

Таким образом, в режиме бегущей волны входное сопротивление любого отрезка нагруженной линии независимо от его длины в точности равно волновому сопротивлению линии.

Амплитуда напряжения (а) и фаза (б) в ЛП при согласованной нагрузке

Холостой ход

В этом случае , , из (14.8.4) следует, что , а это означает, что , =0, 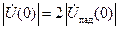, имеет место режим чисто стоячей волны, при наблюдается пучность напряжения и узел тока: 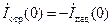. Из (14.5.9), также как из (14.9.1), (14.9.2), следует:

(14.11.3)

откуда

(14.11.4)

Рис. 14.11.2 иллюстрирует соотношения (14.11.3), (14.11.4). Из рисунка и соотношений следует:

в линии устанавливается чисто стоячая волна с пучностью напряжения и узлом тока на конце линии;
напряжение, ток и входное сопротивление периодичны с периодом ;
входное сопротивление чисто мнимое всюду, кроме точек с координатами ;
если длина разомкнутой линии меньше 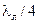, то такая линия эквивалентна емкости;
если длина такой линии равна 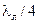, то она эквивалентна последовательному резонансному на данной частоте контуру и имеет нулевое входное сопротивление;
если длина такой линии находится в интервале , то она эквивалентна индуктивности;
если длина такой линии равна , то она эквивалентна параллельному резонансному на данной частоте контуру и имеет бесконечно большое входное сопротивление.

Амплитуды напряжения и тока (верхний рисунок) и реактивное входное сопротивление (нижний рисунок) в ЛП, нагруженной на холостой ход

Короткое замыкание

В этом случае , , из (14.8.4) следует, что , а это означает, что , , , имеет место режим чисто стоячей волны, при наблюдается пучность тока и узел напряжения: . Из (14.5.9), также как из (14.9.1), (14.9.2), следует:

(14.11.5)

откуда

(14.11.6)

Рис. 14.11.3 иллюстрирует соотношения (14.11.5), (14.11.6). Из рисунка и соотношений следует:

в линии устанавливается чисто стоячая волна с пучностью тока и узлом напряжения на конце линии;

напряжение, ток и входное сопротивление периодичны с периодом ;
входное сопротивление чисто мнимое всюду, кроме точек с координатами ;

при длинах замкнутой линии она эквивалентна индуктивности, параллельному на данной частоте контуру, емкости, последовательному на данной частоте контуру, соответственно.

Амплитуды напряжения и тока (верхний рисунок) и реактивное входное сопротивление (нижний рисунок) в ЛП, нагруженной на короткое замыкание

Емкость

Пусть линия нагружена на емкость . В этом случае , . Из (14.8.4) следует, что

(14.11.7)

откуда

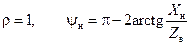(14.11.8)

Подставляя эти формулы в (14.9.1), получаем распределение модуля напряжения вдоль линии:

(14.11.9)

а распределение модуля тока сдвинуто на 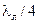(рис. 14.11.4). Таким образом, в этом случае также имеет место режим чисто стоячей волны, но в конце линии нет ни пучности, ни узла. Ближайшими к нагрузке экстремумами будут узел напряжения и пучность тока, они отстоят от конца линии на .

Амплитуды напряжения и тока (верхний рисунок) и реактивное входное сопротивление (нижний рисунок) в ЛП, нагруженной на емкость

Индуктивность

Пусть линия нагружена на индуктивность . В этом случае , . Очевидно, что распределение модулей напряжения и тока, а также входного сопротивления (рис. 14.11.5), будет повторять картину в случае емкостной нагрузки, но со сдвигом в противоположную сторону на , так что ближайшими к нагрузке экстремумами будут пучность напряжения и узел тока.

Амплитуды напряжения и тока (верхний рисунок) и реактивное входное сопротивление (нижний рисунок) в ЛП, нагруженной на индуктивность

Распределение в линии, нагруженной на активное сопротивление, не равное волновому

Пусть , . Как следует из (14.8.4), при коэффициент отражения будет вещественным положительным числом и, как следует из (14.9.1), распределение модуля напряжения вдоль линии:

(14.12.1)

а при будет вещественным отрицательным числом и

(14.12.2)

Назначим какое-либо 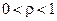и построим зависимость (рис. 14.12.1). Имеет место режим смешанных волн, на конце линии достигаются экстремумы: пучность напряжения и узел тока при , пучность тока и узел напряжения – при .

⇐ Предыдущая 1 2 3 4 5 6 7 89