Предел числовой последовательности.
Последовательность 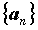 - это функция, заданная на множестве натуральных чисел
- это функция, заданная на множестве натуральных чисел  . Число
. Число 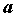 называется пределом последовательности
называется пределом последовательности 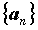 , если для любого положительного числа
, если для любого положительного числа 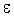 , как бы мало оно ни было, существует такой номер
, как бы мало оно ни было, существует такой номер 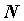 , что для всех
, что для всех 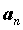 c номерами
c номерами  справедливо неравенство
справедливо неравенство 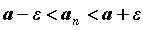 . Неравенство
. Неравенство 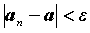 , эквивалентное неравенству
, эквивалентное неравенству 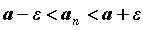 , означает, что для любого
, означает, что для любого 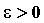 существует такой номер
существует такой номер 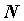 , что все
, что все 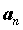 c номерами
c номерами  расположены между
расположены между  и
и 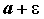 . Последовательность, предел которой - конечное число
. Последовательность, предел которой - конечное число 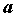 , называется сходящейся, и ее предел обозначают
, называется сходящейся, и ее предел обозначают 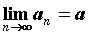 . Если изобразить элементы последовательности
. Если изобразить элементы последовательности 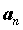 на плоскости точками с координатами
на плоскости точками с координатами 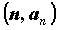 , то неравенства
, то неравенства 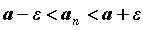 означают, что все точки
означают, что все точки 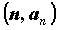 с номерами
с номерами  расположены между параллельными оси абсцисс прямыми
расположены между параллельными оси абсцисс прямыми  и
и 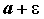 .
.
Бесконечно малая последовательность. Последовательность 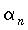 , предел которой равен нулю
, предел которой равен нулю 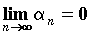 , называется бесконечно малой.
, называется бесконечно малой.
Бесконечно большая последовательность. Последовательность 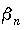 называетсябесконечно большой, если для любого положительного числа
называетсябесконечно большой, если для любого положительного числа 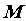 , как бы велико оно ни было, существует такой номер
, как бы велико оно ни было, существует такой номер 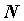 , что для всех
, что для всех 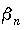 с номерами
с номерами  справедливо неравенство
справедливо неравенство  , записываем
, записываем 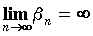 .
.
Предел функции в точке и на бесконечности.
Предел функции по Коши
Значение  называется пределом ( предельным значением ) функции
называется пределом ( предельным значением ) функции 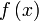 в точке
в точке  , если для любого наперёд взятого положительного числа
, если для любого наперёд взятого положительного числа  найдётся отвечающее ему положительное число
найдётся отвечающее ему положительное число 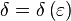 такое, что для всех аргументов
такое, что для всех аргументов  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  .[1]
.[1]

Предел на бесконечности по Коши
· Пусть числовая функция 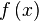 задана на множестве
задана на множестве  , в котором отыщется сколь угодно большой элемент, то есть для всякого положительного
, в котором отыщется сколь угодно большой элемент, то есть для всякого положительного 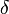 в нём найдётся элемент, лежащий за границами отрезка
в нём найдётся элемент, лежащий за границами отрезка 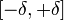 . В этом случае число
. В этом случае число  называется пределом функции
называется пределом функции 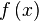 на бесконечности, если для произвольного положительного числа
на бесконечности, если для произвольного положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число 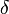 такое, что для всех точек, превышающих
такое, что для всех точек, превышающих 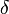 по абсолютному значению, справедливо неравенство
по абсолютному значению, справедливо неравенство  .
.
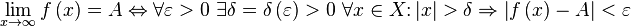
· Пусть числовая функция 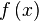 задана на множестве
задана на множестве  , в котором для любого числа
, в котором для любого числа 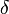 найдётся элемент, лежащий правее него. В этом случае число
найдётся элемент, лежащий правее него. В этом случае число  называется пределом функции
называется пределом функции 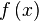 на плюс бесконечности, если для произвольного положительного числа
на плюс бесконечности, если для произвольного положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число 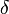 такое, что для всех точек, лежащих правее
такое, что для всех точек, лежащих правее 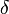 , справедливо неравенство
, справедливо неравенство  .
.
· Пусть числовая функция 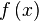 задана на множестве
задана на множестве  , в котором для любого числа
, в котором для любого числа 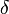 найдётся элемент, лежащий левее него. В этом случае число
найдётся элемент, лежащий левее него. В этом случае число  называется пределом функции
называется пределом функции 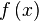 на минус бесконечности, если для произвольного положительного числа
на минус бесконечности, если для произвольного положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число 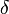 такое, что для всех точек, лежащих левее
такое, что для всех точек, лежащих левее 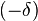 , справедливо неравенство
, справедливо неравенство  .
.
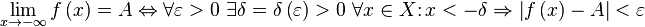
Первый и второй замечательные пределы.
· Первый замечательный предел:
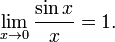
· Второй замечательный предел:
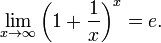
Непрерывность функции в точке на бесконечности. Теорема о непрерывных функциях.
Определение непрерывности функции в точке.
Функция f(x) называется непрерывной в точке 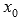 , если предел слева равен пределу справа и совпадает со значением функции в точке
, если предел слева равен пределу справа и совпадает со значением функции в точке 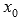 , то есть
, то есть 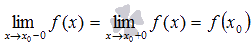 .
.
Теоремы непрерывности
Теорема 1.
Пусть функция f (x) непрерывна в точке x = a, и C является константой. Тогда функция Сf (x) также непрерывна при x = a.
Теорема 2.
Даны две функции f (x) и g (x), непрерывные в точке x = a. Тогда сумма этих функций f (x) + g (x) также непрерывна в точке x = a.
Теорема 3.
Предположим, что две функции f (x) и g (x) непрерывны в точке x = a. Тогда произведение этих функцийf (x) g (x) также непрерывно в точке x = a.
Теорема 4.
Даны две функции f (x) и g (x), непрерывные при x = a. Тогда отношение этих функций  также непрерывно при x = a при условии, что
также непрерывно при x = a при условии, что 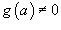 .
.
Теорема 5.
Предположим, что функция f (x) является дифференцируемой в точке x = a. Тогда функция f (x) непрерывна в этой точке (т.е. из дифференцируемости следует непрерывность функции в точке; обратное − неверно).
Теорема 6 (Теорема о предельном значении).
Если функция f (x) непрерывна на закрытом и ограниченном интервале [a, b], то она ограничена сверху и снизу на данном интервале. Другими словами, существуют числа m и M, такие, что
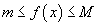
для всех x в интервале [a, b].
Теорема 7 (Теорема о промежуточном значении).
Пусть функция f (x) непрерывна на закрытом и ограниченном интервале [a, b]. Тогда, если c − некоторое число, большее f (a) и меньшее f (b), то существует число x0, такое, что
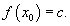
Асимптоты графика функции.
Вертикальная
Вертикальная асимптота — прямая вида 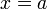 при условии существования предела
при условии существования предела 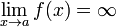 .
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
1. 
2. 
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.
Горизонтальная
Горизонтальная асимптота — прямая вида 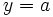 при условии существования предела
при условии существования предела
 .
.
Наклонная
Наклонная асимптота — прямая вида  при условии существования пределов
при условии существования пределов

Пример наклонной асимптоты
1. 
2. 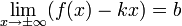
Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!
Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен 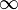 ), то наклонной асимптоты при
), то наклонной асимптоты при  (или
(или 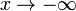 ) не существует!
) не существует!
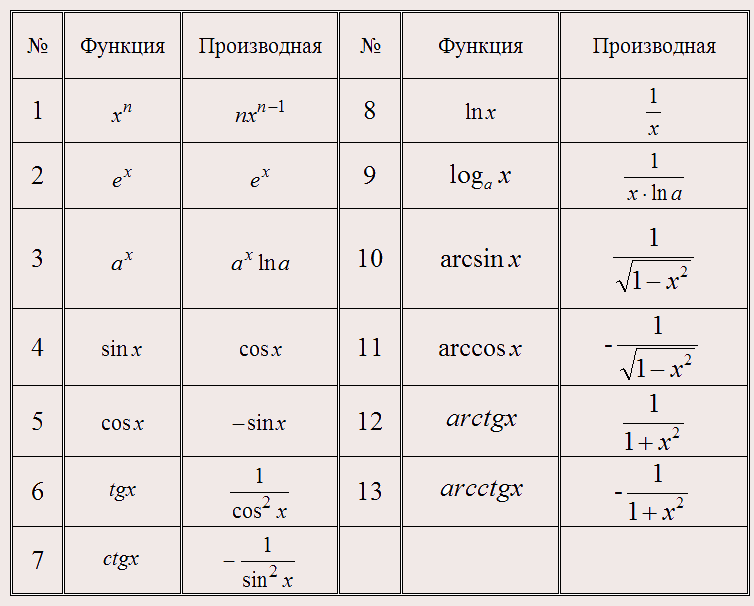
Понятие производной. Правила дифференцирования. Таблица производных.
Производной функции y = f(x) в точке хo называется предел
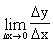 =
= 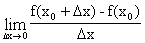
Правила дифференцирования
1) (с) ' = 0, (cu) ' = cu';
2) (u+v)' = u'+v';
3) (uv)' = u'v+v'u;
4) (u/v)' = (u'v-v'u)/v2;
Популярное:

