Полная схема исследования функции и построения ее графика

Общие исследование функции y = f(x).

Область определения функции. Найти ее область определения D(f). Если это не слишком сложно, то полезно найти также область значений E(f). (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)
Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox. Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.
Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определенияD(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
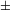
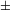
Наклонные и горизонтальные асимптоты. Если область определения D(f) вклоючает в себя лучи вида (a; + ) или (− ; b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x + или x − соответственно, т.е. найтиlimx f(x). Наклонные асимптоты: y = kx + b, где k=limx + xf(x) и b=limx + (f(x)− x). Горизонтальны асимптоты: y = b, гдеlimx f(x)=b.
Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.

Понятие функции многих переменных. Частные и производные. Полный дифференциал.

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции 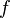определяется следующим образом:

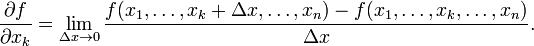
Следует обратить внимание, что обозначение следует понимать как цельный символ, в отличие от обычной производной функции одной переменной , которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции: , где — частный дифференциал функции f по переменной x. Часто непонимание факта цельности символа является причиной ошибок и недоразумений, как, например, сокращение в выражении 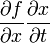. (подробнее см. Фихтенгольц, «Курс дифференциального и интегрального исчисления»).

Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции 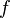в точке по координате равна производной по направлению 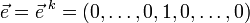, где единица стоит на 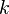-ом месте.

Полный дифференциал

функции f(x, у, z, ...) нескольких независимых переменных — выражение

в случае, когда оно отличается от полного приращения

Δ f=f(x+Δ x, y+Δ y, z+Δ z, …)- f(x, y, z, …)

на величину, бесконечно малую по сравнению с

Локальный экстремум. Условия существования.

Экстре́ мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве.

Определения

Пусть дана функция и — внутренняя точка области определения Тогда

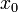· называется точкой локального максимума функции если существует проколотая окрестность такая, что

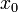· называется точкой локального минимума функции если существует проколотая окрестность такая, что

Если неравенства выше строгие, то 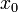называется точкой строгого локального максимума или минимума соответственно.

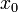· называется точкой абсолютного (глобального) максимума, если

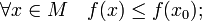
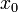· называется точкой абсолютного минимума, если

Значение функции 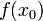называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

⇐ Предыдущая 1 2 34