Условие устойчивости баланса амплитуд

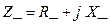Для упрощения анализа амплитудных соотношений будем считать, что в АГ используется безынерционный генераторный прибор (то есть, ), входная, выходная и проходная проводимости которого практически не зависят от и . С учетом сказанного, уравнение равновесия, записанное в форме (4), можно представить, как , где в общем случае . Однако, поскольку – вещественная величина, баланс фаз выполнится на частоте , при которой , а уравнение баланса амплитуд примет вид

. (7)

Амплитуда колебаний в АГ может быть найдена из уравнения (7). Сделанные выше допущения позволяют считать, что нелинейный характер уравнения баланса амплитуд определяется только нелинейной зависимостью 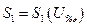. Воспользуемся графическим решением уравнения (7). В этом случае амплитуда напряжения возбуждения в установившемся режиме будет определяться абсциссой точки пересечения кривой 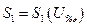с прямой . Зависимости нормированной средней крутизны от амплитуды напряжения возбуждения, вычисленные при кусочно-линейной аппроксимации статических характеристик ГП и различных значениях напряжения смещения , представлены на рис. 2. Поясним ход приведенных кривых.

При и 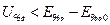(здесь – напряжение запирания) ГП работает в классе А. Его средняя крутизна по первой гармонике равна статической крутизне в выбранной рабочей точке и при кусочно-линейной аппроксимации характеристик ГП не зависит от . Как только превысит величину ( ), появится отсечка в импульсе выходного тока ГП, а средняя крутизна по первой гармонике начнет уменьшаться.

Рис. 2

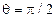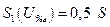При угол отсечки и в области недонапряженного режима не зависит от . Поэтому график представляет собой горизонтальную линию.

Если , то до тех пор, пока не превысит величины , выходной ток ГП будет равен нулю. Будет равна нулю и средняя крутизна. С дальнейшим ростом появится выходной ток, угол отсечки начнет увеличиваться, стремясь к π /2, что будет сопровождаться ростом .

Резкое уменьшение при 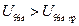объясняется переходом ГП в перенапряженный режим.

Проведем на графике рис. 2 горизонтальные линии через точки с ординатами . В зависимости от выбранных значений возможны следующие случаи взаимного расположения графиков. Если , баланс амплитуд может быть выполнен только при , а возможное значение (точка «a»), соответствующее состоянию равновесия – единственно. Если же , условие баланса амплитуд выполняется только для 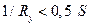и при двух возможных значениях , соответствующих абсциссам точек «b» и «c» на рис.2.

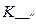Для исследования устойчивости баланса амплитуд в полученных точках равновесия поступим следующим образом. Введем понятие суммарного коэффициента передачи . В общем случае зависит не только от амплитуды и частоты существующих колебаний, но и от воздействующих на АГ внешних дестабилизирующих факторов. К таким факторам можно отнести давление, температуру и влажность окружающей среды, механические, динамические и статические нагрузки, изменение напряжения источников питания и т.п. Под их воздействием могут меняться как параметры ГП, так и КС.

Будем считать состояние равновесия в АГ устойчивым по амплитуде, если при изменении внешних воздействий, нарушающих баланс амплитуд, произойдет такое изменение амплитуды колебаний, что состояние равновесия вновь восстановится, чему соответствует выполнение неравенства:

или

. (8)

При этом, чем больше , тем меньшие изменения амплитуды колебаний потребуются для восстановления баланса амплитуд. Если ГП работает в недонапряженном режиме, увеличение достигается за счет уменьшения угла отсечки θ . Используя условие (8), нетрудно убедиться, что на графиках рис. 2 точки равновесия «a», «c» и «d» устойчивы, а точка «b» – неустойчива.

Если , то при баланс амплитуд не выполнен, т.к. . Поэтому при включении АГ сколь угодно малые флуктуации напряжения на входном электроде ГП приведут к возрастанию амплитуды колебаний до установившегося значения, соответствующего стационарному режиму. Процесс возникновения колебаний в АГ в этом случае носит название «мягкого» самовозбуждения. При этом, если ( 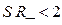), ограничение роста амплитуды колебаний обусловлено падением средней крутизны за счет уменьшения угла отсечки . При ограничение амплитуды колебаний происходит за счет перехода ГП автогенератора в перенапряженный режим.

При и в точке . Поэтому любые флуктуации входного напряжения с амплитудой меньше абсциссы точки неустойчивого равновесия ( точки «b» на рис. 2) будут затухать. При переходе в стационарное состояние с необходимо внешнее воздействие, амплитуда которого больше абсциссы точки неустойчивого равновесия. В данном случае имеет место режим «жесткого» самовозбуждения, а ограничение амплитуды колебаний осуществляется за счет падения крутизны с возрастанием напряженности режима. Таким образом, в любом случае устойчивость стационарного состояния и ограничение амплитуды колебаний в АГ определяются нелинейными свойствами ГП и, в частности, уменьшением с ростом при уменьшении угла отсечки или при переходе в перенапряженный режим.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Популярное:

1. Абсолютные и относительные показатели финансовой устойчивости предприятия
2. Актива Бухгалтерского баланса
3. Амплитуда защит, пространственный уровень контрзащит
4. Амплитудно-частотная и фазочастотная характеристики
5. Взаимоувязка показателей Бухгалтерского баланса
6. Вначале организация проводит реформацию баланса и списывает прибыль после уплаты налогов проводкой: Дебет 99 Кредит 84.
7. Водные ресурсы Западной Европы. Анализ водохозяйственного баланса европейских стран
8. ВОПРОС 51. Спрос на общественные блага и условие их оптимального предоставления. Проблема безбилетника.
9. Выполнение практикума является условием получения допуска к зачету.
10. ГЛАВА 2. АНАЛИЗ КОНФЛИКТНОСТИ И СТРЕССОУСТОЙЧИВОСТИ ПЕРСОНАЛА В КАФЕ-БАРЕ «УЛЬТРАФИОЛЕТ»
11. Глава 4. Анализ устойчивости объекта против террористических проявлений
12. Глава вторая: подчиняться положениям Ислама есть условие действительности Ислама.