Геометрия аффинной плоскости с проективной точки зрения.

Прежде всего рассмотрим проективную прямую P¹, вложенную в расширенную плоскость.

Обсудим отличие аффинной прямой от проективной. Ясно, что проективная прямая имеет на одну точку больше, чем аффинная. Напомним, что координатой точки M аффинной прямой в репере (A, e ) называется такое число x, что = x e .

Лемма. Пусть на расширенной прямой выбраны репер R = (A, B_∞, E), где B_∞ - несобственная точка, и собственная точка M, имеющая в репере R координаты (x¹, x²). Тогда точка M в аффинном репере (A, ) аффинной прямой d имеет координату .

Доказательство. Возьмем собственную точку O расширенной плоскости, не лежащую на прямой . Пусть x - аффинная координата точки M в репере (A, ), то есть = x .

Пусть вектор

параллелен прямой d и

. Система векторов

согласована и порождает точки проективного репера R = (A, B_∞, E), заметим, что

. Поскольку

= x

, то

+ x

. Вектор

порождает точку M, поэтому числа (1, x) являются координатами точки M в репере R. По условию леммы (x¹, x²) также координаты точки M, следовательно (1, x) и (x¹, x²) пропорциональны, т.е. x=

, что и требовалось доказать.

Обобщим конструкцию на случай репера, заданного на расширенной плоскости . Пусть на задан репер R = (A, Х_∞, Y_∞, E), где точки A и E - собственные, а X_∞, Y_∞ - бесконечно удаленные.

Пусть E₃= (AX_∞) ∩ (Y_∞ E), E₂= (A Y_∞) ∩ (X_∞ E). Если M_∞ есть какая-либо несобственная точка расширенной плоскости, то она принадлежит бесконечно удаленной координатной прямой (X_∞ Y_∞), и имеет координаты (0, x², x³). Если N(y¹, y², y³) – собственная точка, то y¹≠ 0. Положим e₁ = и e₂ = , тогда на аффинной плоскости = e₁ + e₂.

Рассмотрим аффинный репер R₀ = (A, e₁, e₂ ), пусть в этом репере точка N имеет координаты (x, y). Используя результат леммы, имеем x = , y = .

Рассмотрим множество H всех проективных преобразований расширенной плоскости, переводящих несобственную прямую (Х_∞ Y_∞) в себя, H есть подгруппа группы всех проективных преобразований плоскости. Пусть f H, запишем аналитическое выражение преобразования f в репере Â = (A, Х_∞, У_∞, E):

(1)

Бесконечно удаленная прямая имеет уравнение x³=0 и при преобразовании f переходит в себя, следовательно, = 0, = 0. В формулах (1) ρ ≠ 0, ≠ 0, ≠ 0.

Разделив почленно первое и второе равенства в (1) на третье, получаем

, где = , i, j = 1, 2, ≠ 0.

Группа аффинных преобразований аффинной плоскости изоморфна H, таким образом, аффинную геометрию на плоскости можно рассматривать как геометрию, изучающую свойства фигур, инвариантных относительно группы H.

Приложение 1

Ответы, указания, решения задач к главам 1, 2, 3.

Задача 1. Если прямая , то точка не имеет образа.

Задача 2. Поле , т.е. состоит из двух элементов. Операции сложения и умножения задаются таблицами

+

соcтоит из всевозможных линейных комбинаций , где , , ( , 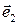– базисные векторы). Как множество содержит ровно три элемента: , которые попарно неколлинеарны и поэтому порождают ровно три точки проективной прямой .

Задача 3. состоит из всевозможных линейных комбинаций , где , , – базис . содержит ровно семь элементов , , 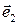, , , , , которые попарно неколлинеарны и поэтому порождают ровно семь точек .

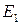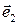Введем обозначения: , , , , , , , где . , так как вектор , порождающий точку , принадлежит двумерному векторному подпространству, порождающему прямую . Аналогично, , . Очевидно, не принадлежит ни одной из прямых , , в силу того, что любые три из четверки векторов , , , некомпланарны. , , (подумайте почему). Имеем шесть прямых (рис. 26 ) и седьмую (необозначенную на рисунке), проходящую через точки 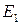, , 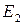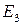( векторы . , очевидно компланарны, т.к. , поскольку 1+1 =0).

Рис. 26

Задача 4. Пусть – базис трехмерного векторного пространства над полем , порождающего . Векторы , , 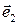, попарно неколлинеарны и поэтому порождают четыре различные точки. Так как никакие три вектора из этой четверки векторов некомпланарны, то никакие три точки не лежат на одной прямой.

Задача 5. . Пусть порождает прямую плоскости . как множество состоит из следующих элементов: { , , 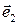, , , }. Векторы , и , коллинеарны. Имеем четверку попарно неколлинеарных векторов , , 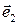, , которые порождают ровно четыре различные точки проективной прямой .

Задача 6. . Пусть – базис , порождающего . как множество состоит из линейных комбинаций векторов вида , где . Так как может принимать различных значений, то имеется ровно различных элементов в . В будет соответственно на один элемент меньше, т.е. , но не все они будут попарно неколлинеарны. Каждый вектор входит в это множество вместе с семейством коллинеарных векторов вида , . Таким образом, имеется ровно попарно неколлинеарных векторов в , которые порождают точку.

Задача 7. Так как прямая имеет размерность , то из предыдущей задачи получаем, что прямая содержит различную точку.

Задача 8. будет иметь наименьшее число точек, если поле будет тривиальным, т.е. состоять из двух элементов – нуля и единицы. , порождающее , будет состоять из всевозможных линейных комбинаций базисных векторов, т.е. из векторов вида , где . Получаем, что будет состоять из попарно неколлинеарных векторов, порождающих 15 различных точек .

Задача 9. Построим точку . Рассмотрим пучок прямых с центром в точке . Возьмем вектор , параллельный прямой и разложим его по прямым и . Получим . Система векторов , , согласована относительно репера . Построим вектор и прямую . Тогда в соответствии с определением проективных координат . Аналогично строится точка . Точки и совпадают, т.к. их координаты пропорциональны.

Задача 10. Возьмем вектор с началом в точке и разложим его по прямым и . Если обозначить через и его составляющие, то и система векторов , , согласована относительно проективного репера . Строим вектор . Тогда прямая пучка, параллельная вектору , будет искомой прямой .

Рис.27

Задача 11. Пусть, например, – несобственная точка расширенной прямой . Рассмотрим пучок прямых с центром в т. . Разложим вектор по прямым и , где . Тогда . Система векторов , , – согласована относительно репера . Пусть . Построим вектор . Тогда , где .

Можно и по-другому: если , то в аффинной системе координат точка имеет координату .

Рис.28

Задача 12. Возьмем собственную точку расширенной плоскости, не лежащую на . , т.к. – середина отрезка . Система векторов , , согласована относительно репера . Вектор порождает точку . Следовательно, , или иначе .

Рис. 29.

Задача 13. На прямой 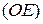возьмем ненулевой вектор и разложим его по правилу параллелограмма на сумму базисных векторов и , лежащих на прямых (ОA₁) и (ОA₂). Тогда , , , (подумайте почему). Аффинный репер 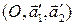порождает тот же проективный репер . Векторы и коллинеарны и порождают одну и ту же точку прямой .

Задача 14. Пусть – аффинный репер, порождающий проективный репер . Тогда , , , , где , , . Обозначим , . Тогда из определения простого отношения трех точек имеем: , .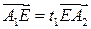

Так как векторы и равны, то равны их координаты относительно базиса :

откуда , , . Аналогично,

Из равенства имеем:

или

Откуда

Рис. 30

Задача 15. Точка , т.к. третья ее координата равна 0. В репере точка имеет координаты , т.е. . Таким образом, задача сводится к ранее рассмотренной задаче построения точки на расширенной прямой по ее координатам в репере на этой прямой. Аналогично, , где . Для построения точки найдем сначала ее проекции 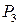и на прямые и соответственно из центров и . , . Получаем . .

Рис. 31

Задача 16. Пусть – проекция на из центра . Тогда , где . 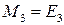, т.к. система векторов , , согласована относительно . Пусть – проекция на из центра . Тогда , где . Система векторов , , согласована относительно . Вектор параллелен прямой , поэтому – несобственная точка расширенной прямой . Таким образом, является точкой пересечения прямой с прямой, параллельной и проходящей через точку .

Рис. 32

Задача 17. Уравнение прямой : . Очевидно , где , . и , где . Аналогично, и , где . Строим точки и по их координатам в соответствующих реперах на расширенных прямых и получаем .

Задача 18. Рассмотрим случай, когда три прямые попарно различны. Пусть . Напомним, что любые две прямые на расширенной плоскости пересекаются в собственной или несобственной точке. Общее уравнение системы из двух однородных линейных уравнений

Имеет вид:

, , , .

Нас интересует случай, когда . 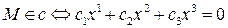, т.е. тогда и только тогда, когда

Окончательно, прямые проходят через одну точку в том и только том случае, когда

19. а) Запишем матрицу перехода от репера к :

Столбцы этой матрицы согласованы. Получаем формулы преобразования проективных координат:

б) Запишем матрицу перехода от репера к :

Столбцы этой матрицы не согласованы. Для согласования решаем систему линейных уравнений:

Получаем , , .

Согласованная матрица перехода имеет вид:

Записываем формулы преобразования проективных координат:

Задача 20. Указание. Построить невырожденную конфигурацию Дезарга, разместив деревья в точках , , , , , , , , , .

Задача 21. Построим треугольники и так, чтобы точки и лежали на прямой , точки и на прямой и чтобы соответственные стороны треугольников пересекались в точках на прямой . Тогда в силу обратной теоремы Дезарга прямая пройдет через .

Построение. Берем произвольные точки и на прямой и точку на прямой . Строим треугольник и проводим произвольную прямую , не проходящую через , , , . Получаем: , , , . Точку получаем как пересечение ( ) и ( ). Проводим ( ).

Рис.33

Задача 22. Указание. Имеем здесь частный случай предыдущей задачи, когда и параллельны.

Задача 23. Рассмотрим треугольники и . Прямые , и параллельные, а значит имеют общую несобственную точку на расширенной плоскости. Таким образом, мы находимся в условиях теоремы Дезарга (два трехвершинника и имеют центр перспективы). Следовательно, точки , , 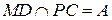лежат на одной прямой.

Рис.34

Задача 24. Рассмотрим два треугольника и . , , . Так как , то – несобственная точка прямых , и . Следовательно, . Таким образом, мы находимся в условиях обратной теоремы Дезарга для трехвершинников и (они имеют ось перспективы). Следовательно, они имеют и центр перспективы, т.е. прямые , , 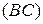принадлежат одному пучку.

Задача 25.

и т.д.

Задача 26. Рассмотрим проективный репер и пусть , . Тогда , .

откуда и следует утверждение задачи.

Задача 27. Проведем прямую , не проходящую через точку . Обозначим 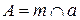, , , . По условию – биссектриса внутреннего угла треугольника, – биссектриса внешнего угла треугольника при вершине .

Отсюда , . Получаем:

Рис. 35

Задача 28. Обозначим .

, т.к. , т.е. .

Рис. 36

Задача 29. Обозначим . Тогда

, т.к. – середина отрезка .

Рис. 37

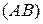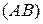Задача 30. Пусть – несобственная точка расширенной прямой . Тогда ( – середина отрезка ), т.е. точки , гармонически разделяют пару точек , . Построим полный четырехвершинник так, чтобы и были диагональными точками, – точкой пересечения со стороной, проходящей через третью диагональную точку. Тогда по свойству

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒