Расчёт на вертикальную нагрузку от мостовых кранов.

Т=4.59 т

Основная система, эпюра М₁, каноническое уравнение, коэффициент такие же как и при расчёте на вертикальную нагрузку мостовых кранов.

Моменты и реакции в основной системе от силы Т:

-0.1·4.59·17.6=-8.08

-0.106·4.59·17.6=-8.56

0.104·4.59·17.6=8.4

0.711·4.59=3.26

Смещение верхних концов с учетом пространственной работы

0.817·3.263/0.714=3.73/t

Эпюра моментов ( )

MA=-4.341t*3.734/t=-16.209

MB=1.945t*3.734/t=7.263

MC=0.122t*3.734/t=0.4555

Суммарная эпюра ( )

Левая колонна:

MA=-8.078+(-16.21)=-24.29т*м

MB=-8.563+7.263=-1.3т*м

MC=8.402+0.456=8.86т*м

Правая колонна:

MA= -16.21т*м

MB= 7.263т*м

MC= 0.456т*м

Qвс л= –(–-1.3+8.86)/5.2=-1.95

Qас л=(8.86–-24.288)/12.4=2.67

Qас пр=(7.263–(-16.21))/17.6=1.33

Проверка правильности решения: скачок на эпюре Q= 2.67–(-1.95)=4.62- равно горизонтальной реакции T= 4.59

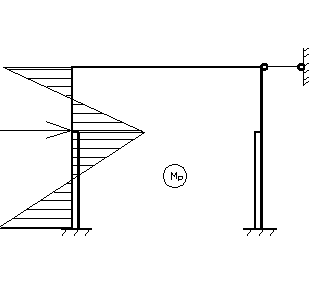
Расчёт на ветровую нагрузку.

Основная система и эпюра М₁ такие же как и для крановых воздействий.

Эпюра М_P на левой стойке:

-0.1037*0.46*17.6² =-14.78

-0.056*0.46*17.6² =-7.98

0.034*0.46*17.6² =4.84

0.461*0.46*17.6=3.73

На правой стойке усилия получаются умножением на коэффициент

0.35/0.46=0.76

Усилия на правой стойке

-14.78·0.761=-11.25т*м

-7.98·0.761=-6.07т*м

4.84·0.761=3.68т*м

3.73·0.761=2.84т*м

Коэффициенты канонического уравнения по формуле (12.22)

0.714t

3.73+2.839+2.095+1.571=10.24

Смещение рамы

10.235/0.714t=14.335/t

Эпюра моментов ( )

-4.34t*14.335/t=-62.214

1.95·14.335=27.95

0.12·14.335=1.72

Суммарная эпюра ( )

Левая колонна:

-14.78+-62.214=-76.99т*м

-7.98+27.95325=19.97т*м

4.84+1.7202=6.56т*м

Правая колонна:

-11.24758+-62.214=-73.46т*м

-6.07278+27.95325=21.88т*м

3.68324+1.7202=5.4т*м

Эпюра Q на левой стойке

(–-76.994+19.97)/17.6+0.46·17.6/2=9.56

9.557–0.46·17.6=1.46

Эпюра Q на правой стойке

(–-73.46+21.88)/17.6+0.35·17.6/2=8.5

8.497–0.35·17.6=2.34

При правильном решении сумма поперечных сил внизу должна быть равна сумме всех горизонтальных нагрузок

9.557+8.497=18.05

(0.46+0.35)·17.6+2.095+1.571=17.92

1.461+2.337=3.8

2.095+1.571=3.67

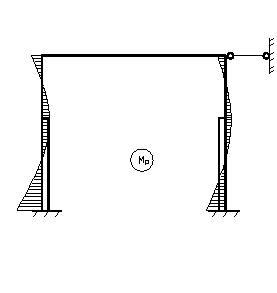
Сочетания нагрузок

Определив в раме изгибающие моменты и нормальные силы от каждой из расчетных нагрузок, необходимо найти их наиболее невыгодные сочетания, которые могут быть неодинаковыми для разных сечений элементов рамы.

При составлении основных сочетаний учитываются:

- постоянные нагрузки, плюс временные длительные нагрузки, плюс одна кратковременная с коэффициентом сочетаний, равным единице;

- постоянные и временные длительные нагрузки, плюс не менее двух кратковременных нагрузок, с коэффициентом сочетаний 0, 9 каждая;

4. Комбинации нагрузок (т*м)

Расчет ступенчатой колонны

5.1. Исходные данные.

Требуется подобрать сечения сплошной верхней и сквозной нижней частей колонны однопролётного производственного здания (ригель имеет жёсткое сопряжение с колонной).

Для верхней части колонны

в сечении 1—1 N= 80.84; М= 109.5 т× м;

в сечении 2—2 N= 105.8 т; M= 47.37 т× м;

Для нижней части колонны

N₁= 232.48 т; M₁= -68.402т× м (изгибающий момент догружает подкрановую ветвь);

N₂= 284.32 кН; M₂= 118.07 т× м (изгибающий момент догружает наружную ветвь);

Q_max= 18.365 т

Соотношение жесткостей верхней и нижней частей колонны I_в/I_н=1/5; материал колонны—сталь марки С345, бетон фундамента марки B15.

5.2. Определение расчётных длин колонны.

Расчетные длины для верхней и нижней частей колонны в плоскости рамы определим по формулам и .

Коэффициенты расчетной длины m₁ для нижнего участка одноступенчатой колонны следует принимать в зависимости от отношения и величины

(В однопролетной раме с жестким сопряжением ригеля с колонной верхний конец колонны закреплен только от поворота по табл 68

(167) (СНиП «СК»)

F₁-сила приложенная к колонне в уступе

F₂ – сила приложенная к колонне в верхнем узле

l₁ — высота нижней части колонны

l₂ — высота верхней части колонны

I₁ — момент инерции сечения нижней части колонны (I_H)

I₂ — момент инерции сечения верхней части колонны (I_B)

тогда

F₁=F₂ из расчета на постоянные нагрузки (сила в нижней части) F₁= 105.8 т

F₂=F₁ из расчета на постоянные нагрузки (сила в верхней части) F₂= 80.84 т

(5.2/12.4)·(5/2.31)^0.5=0.62

(105.8+80.84)/80.84=2.31

=0.2·(12.4/5.2)=0.48

по таблице 68[1] для одноступенчатых колонн с верхним концом, закрепленным только от поворота находим коэффициент: 1.806

1.806/0.617=2.93

= 1.806·12.4=22.39

= 2.93·5.2=15.24

Расчетные длины из плоскости рамы для нижней и верхней частей равны соответственно

12.4м

5.2–1.4=3.8 м

5.3. Подбор сечения верхней части колонны.

Сечение верхней части колонны прини­маем в виде сварного двутавра высотой

h_в = 100 см.

По формуле (14.14) (Веденников) определим требуемую площадь сечения, предварительно определив приближенные значения характеристик.

Для симметричного двутавра 0.42·100=42

r_x»0, 35h=0, 35× 100=35см;

(15.236·100/42)·(3200/2060000)^0.5=1.43

(для листов из стали С345 толщи­ной до до 20мм R_Y= 3200 кг/см²);

109.5·100/(80.84·35)=3.87

Значение коэффициента по СНиП II-23-81*

(1.9–0.1·3.87)–0.02·(6–3.87)·1.43=1.45

1.452·3.87=5.62

По СНиП II-23-81* таб.74 при 1.43 и 5.6192

0.24

80.84·1000/(0.24·3200·0.95)=110.8

5.4. Компоновка сечения

Высота стенки h_ст=h_B-2t_п= 100–2·2=96 см (принимаем предварительно толщину полок t_п= см).

По формуле 14.2 (Беленя) при m> 1 и l≤ 0, 8 из условия местной устойчивости:

Поскольку сечение с такой толстой стенкой неэкономично, принимаем t_сп=1см и включаем в расчётную площадь сечения колонны два участка стенки шириной по:

0.85·0.8·(2060000/3200)^0.5=17.25

Требуемая площадь полки

(110.8–2·0.85·(0.8^2)·(2060000/3200)^0.5)/2=41.6

Из условия устойчивости верхней части колонны из плоскости действия момента ширина полки b_п³ l_y2/20 = 3.8·100/20=19

из условия местной устойчивости полки по формуле (14.16) (Вед)

,

(0.36+0.1·1.43)·(2060000/3200)^0.5=12.76

где

Принимаем b_п= 32 см; t_п= 2 см;

32·2=64> 41.598 см2

(32–2)/(2·2)=7.5 < 12.762

Геометрические характеристики сечения

Полная площадь сечения 2·32·2+0.8·96=204.8

расчётная часть сечения с учётом только устойчивой части стенки:

2·32·2+2·(0.8^2)·0.85·(2060000/3200)^0.5=155.6

0.8*96³ /12+2*(32*2³ /12+64*(96/2+2/2)² )=366353.07

96*0.8³ /12+2*2*32³ /12=10926.76 см4

366353.07/((96+2·2)/2)=7327.06 см3

7327.06/204.8=35.78 см

(366353.07/204.8)^0.5=42.29см

(10926.76/204.8)^0.5=7.3см

Проверка устойчивости верхней части колонны в плоскости действия момента по формуле 14.9 (Беленя):

, где

φ _х – коэффициент снижения расчётного сопротивления при внецентрнноь сжатии зависит от условной гибкости стержня.

Гибкость стержня 15.236·100/42.29=36.03

36.027·(3200/2060000)^0.5=1.42

= 109.5·100/(80.84·35.78)=3.79

2·32/(0.8·96)=0.83

Значение коэффициента h определяем по прил.10 (Беленя):

(1.75–0.1·3.79)–0.02·(5–3.79)·1.42=1.34

1.337·3.79=5.07

0.241

109.5·1000/(0.241·155.6)=2920.03кг/см2< Ry=3200·0.95=3040кг/см2

условие выполняется.

Проверка устойчивости верхней части колонны из плоскости действия момента по формуле 14.10(Беленя):

3.8·100/7.3=52.05

52.05·(3200/2060000)^0.5=2.05

φ _у= 0.812

Для определения m_x найдем максимальный момент в средней трети расчетной дли­ны

47.37+((109.5–47.37)/3.8)·(3.8–1/(3·3.8))=108.07

По модулю: 80.84/2=40.42 т× м;

108.07·100·204.8/(80.84·7327.06)=3.74

при коэффициент где

С – коэффициент учитывающий влияние момента M_X при изгибо-крутильной форме потери устойчивости;

Значения α и β определим по прил.11:

52.05 3.14·(2060000/3200)^0.5=79.67

β =1

При двутавровом сечении балки и

0.65+0.05·3.737=0.84

1/(1+0.71·3.737)=0.27

96/0.8=120 3.8·(2060000/3200)^0.5=96.41

в расчётное сечение включаем только устойчивую часть стенки;

80.84·1000/(0.274·0.812·155.6)=2335.12кг/см2< Ry=3200·0.95=3040кг/см2

5.5. Подбор сечения нижней части колонны.

Сечение нижней части колонны сквозное, состоящее из двух ветвей, соединенных решеткой. Высота сечения h_н= 1500мм. Подкрановую ветвь колонны принимаем из широкополочного двутавра, наружную - составного сварного сечения из трех листов.

Определим по формуле (14.32) ориентировочное положение центра тяжести. При­нимаем z₀=5 см; h₀=h_н-z₀==150-5=145 см;

(118.071/(118.071+(–-68.402)))·145=91.81

y₂=h₀–y₁= 145–91.811=53.19

Усилия в ветвях определим по формулам (14.19) и (14.20).

В подкрановой ветви (232.48)·53.189/145+(–-68.402·100/145)=132.45т

В наружной ветви 284.32·91.811/145+118.071·100/145=261.45 т

По формулам (14.26) определяем требуемую площадь ветвей и назначаем сечение.

Для подкрановой ветви ; задаёмся φ =0, 7, тогда

=132.45·1000·0.95/(0.7·3200)=56.17 см2

По сортаменту (прил. 14) подбираем двутавр 40Б1СТО АСЧМ 20-93;

А_в1= 72.16 см²; i_у= 20020 см; i_х= 4.48 см.

Для наружной ветви

261.454·1000·0.95/(0.7·3200)=110.88

Для удобства прикрепления элементов решетки высоту принимаем таким же, как в подкрановой ветви ( см).

Толщину стенки швеллера t_ст для удобства ее соединения встык с полкой надкрановой части колонны принимаем равной 2 см; высота стенки из условия размещения сварных швов h_ст= 45см.

Требуемая площадь полок

(110.88–2·45)/2=10.44

Из условия местной устойчивости полки швеллера .

Принимаем b_п= 16см; t_п= 2 см; А_п= 32 см².

Геометрические характеристики ветви:

2·45+2·16·2=154 см2

(2·45·(2/2)+2·32·(2+16/2))/154=4.74см

(45*2³ )/12+2*45*(4.74-2/2)² +2*((2*16³ )/12+2*16*5.26)=4424.94см4

(2*45³ )/12+2*((16*2³ )/12+32*18.8² )=37828.99см4

(4424.94/154)^0.5=5.36см

(37828.99/154)^0.5=15.67 см

Уточняем положение центра тяжести сечения колонны:

150–4.74=145.26 см

154·145.26/(72.16+154)=98.91 см

145.26–98.912=46.35см

Данные значения очень близки к первоначальным и поэтому перерасчет не производим.

Проверка устойчивости ветвей из плоскости рамы ly=1500см

Подкрановая ветвь:

1240/16.66=74.43

0.654

132.45·1000/(0.654·72.16)=2806.58 кг/см2

Наружная ветвь

1240/15.67=79.13

0.614

261.454·1000/(0.614·154)=2765.07< 3200·0.95=3040кг/см2

Из условия равноустойчивости подкрановой ветви в плоскости и из плоскости рамы определяем требуемое расстояние между узлами решетки

74.43

74.43·4.48=333.45

Принято =300 см, разделив нижнюю часть на целое число панелей.

Проверяем устойчивость ветвей в плоскости рамы (относительно осей X₁-X₁ , Y₁ – Y₁).

Для подкрановой ветви

= 283/4.48=63.17

0.744

132.45·1000/(0.744·72.16)=2467.08< 3200·0.95=3040кг/см2

Для наружной ветви

= 283/5.36=52.8

0.808

261.454·1000/(0.808·154)=2101.18< 3200·0.95=3040кг/см2

Устойчивость ветвей колонны обеспечена.

5.6. Расчёт решётки подкрановой части колонны.

Поперечная сила в сечении колонны Q_max= 18.365 т

Расчетная схема траверсы

Условная поперечная сила вычисляем по формуле 23*[2]

Q_fic = 7, 15 × 10^-6 (2330–E/R_y)N/j,

(7.15/(1000000))·(2330–(2.1·1000000)/3200)·(284.32·1000/0.744)=4573.31=4.57т< 18.365т

Расчёт решетки проводим на Q_max.

Усилие сжатия в раскосе

18.365/(2·0.686)=13.39 т

1.415/2.06=0.69

Lr=(1.5^2+1.415^2)^0.5=2.06

13.386·1000/(0.542·3200·0.75)=10.29 см2

γ _с=0, 75(сжатый уголок, прикрепляемый одной полкой).

Принимаем L100x7

13.75 см2

1.98 см

(1.5^2+1.415^2)^0.5=2.06

2.06·100/1.98=104.04

0.427

13.386·1000/(0.427·13.75)=2279.92< 3200·0.95=3040кг/см2

Проверка устойчивости колонны в плоскости действия момента как единого стерж­ня по формуле (14.9).

Геометрические характеристики всего сечения:

72.16+154=226.16см2

1446.9+72.16·98.912^2+37828.99+154·46.348^2=1076072.41 см4

(1076072.41/226.16)^0.5=68.98

22.3944·100/68.978=32.47

Приведённая гибкость

2·13.75=27.5

(32.466^2+27·226.16/27.5)^0.5=35.72

35.722·(3200/2060000)^0.5=1.41

Для комбинации усилий догружающих наружную ветвь (сечение 4-4),

N₂= 284.32 т, M₂= 118.071 т× м;

118.071·100·226.16·(46.348+4.74)/(284.32·1076072.41)=0.45

по найденным по и m_X находим =

Находим =0.635;

284.32·1000/(0.635·226.16)=1979.78< 3200·0.95=3040кг/см2

Для комбинации усилий догружающих подкрановую ветвь (сечение 3 – 3)

N₁= 232.48, M₁= 68.402 т*м;

68.402·100·226.16·98.912/(232.48·1076072.41)=0.61

Находим = 0.57

232.48·1000/(0.57·226.16)=1803.41< 3200·0.95=3040кг/см2

Устойчивость сквозной колонны как единого стержня из плоскости действия момента проверять не нужно, так как она обеспечена проверкой устойчивости отдельных ветвей.

5.7. Расчёт и конструирование узла сопряжения верхней и нижней частей колонны.

Расчётные комбинации усилий в сечении над уступом:

1) M= 17.89 т*м; N= 53.96 (загружение 1, 3, 4);

2) M= -47.367 т*м; N= 105.8 т (загружение 1, 2, 5*);

Давление кранов D_mах= 140.37 кН.

Прочность стыкового шва (W1) проверяем в крайних точках сечения надкрановой части.

Площадь шва равна площади сечения колонны.

Первая комбинация M и N:

Наружная полка: ,

53.96·1000/204.8+17.89·100000/7327.06=507.64< 3200·0.95=3040кг/см2

Внутренняя полка:

53.96·1000/204.8–17.89·100000/7327.06=19.31< 3200·0.95=3040кг/см2

Вторая комбинация M и N:

Наружная полка:

s= 105.8·1000/204.8+-47.367·100000/7327.06=-129.87< 3200·0.95=3040кг/см2

Внутренняя полка:

s= 105.8·1000/204.8+-47.367·100000/7327.06=-129.87< 3200·0.95=3040кг/см2

Толщину стенки траверсы определяем из условия ее смятия по формуле (14.28):

4800/1.025=4682.93

- коэффициент надежности по табл.2* [2]

140.37·1000/(34·4682.93)=0.88 см

Принимаем t_тр=1см.

Усилие во внутренней полке верхней части колонны (2-я комбинация)

105.8·1000/2–-47.367/100=52900.47

Длина шва крепления вертикального ребра траверсы к стенке траверсы (ш2)

Принимаем полуавтоматическую сварку проволокой марки СВ-08А d=2мм . Назначаем k_F = 7мм;

1800 кг/см2

4800·0.45=2160 кг/см2

0.9·1800=1620 < 1.05·2160=2268

52900.47/(4·0.7·1620)=11.66

В стенке подкрановой ветви делаем прорезь, в которую заводим стенку траверсы

Для расчёта шва крепления траверсы к подкрановой ветви (ш3) составляем комбинацию усилий дающую наибольшую реакцию траверсы. N= 105.8 т, M= -47.37т

105.8·100/(2·150)–-47.37·100/150+140.37·0.9=193.18т

Коэффициент учитывает, что усилия N и M приняты для 2-го основного сочетания нагрузок. Требуемая длина шва (K_F=0, 7см)

193.18·1000/(4·0.7·1620)=42.59

Из условия прочности стенки подкрановой ветви в месте крепления траверсы (линия 1-1) определим высоту траверсы h_TP по формуле (14.31):

= 193.18·1000/(2·0.7·1810.732)=76.2

0.58·3200/1.025=1810.73

0.7 см- толщина стенки двутавра 40Б1СТО АСЧМ 20-93

Принимаем h_TP= 80 см.

Проверим прочность траверсы как балки, нагруженной усилиями N, M и D_mах. Нижний пояс принимаем конструктивно из листа 450х10, верхние горизонтальные ребра – из двух листов 100х10 мм.

Геометрические характеристики траверсы:

ун=(2·10·1·(1+80–1.5–1/2)+80·1·(1+80/2)+45·1·(1/2))/(2·10·1+80·1+1·45)=33.67

Ix=2*((10*1³ )/12+10*1*45.33² )+((1*80³ )/12+80*1*7.33² )+((45*1³ )/12+45*1*33.17² )=137577.77

137577.77/33.67=4086.06

Максимальный изгибающий момент возникает в траверсе при 2-й комбинации усилий:

(–-47.37·1000·100/150+105.8·1000·100/300)·50=3342333.33

3342333.333/4086.06=817.98< 3200·0.95=3040кг/см2

Максимальная поперечная сила в траверсе с учетом усилия от кранов возникает при комбинации усилий 1, 2, 3, 4(-), 5*

105.8·100/300–(-47.37/150)+1.2·0.9·140.37/2=111.38

111.382·1000/(1.2·80)=1160.23< 1810.7 кг/см2

5.8. Расчёт и конструирование базы колонны.

Ширина нижней части колонны превышает 1 м, поэтому проектируем базу раздельного типа.

Расчётные комбинации усилий в нижнем сечении колонны (сечение 4-4)

1) M= 118.07 т*м; N= 284.32 т (для расчёта базы наружной ветви);

2) M= -68.4 т× м; N= 232.48 т (для расчёта базы подкрановой ветви).

Усилия в ветвях колонны определим по формулам (14.19 и 14.20):

–-68.4·100/145.26+232.48·46.348/145.26=121.27 т

118.07·100/145.26+284.32·46.348/145.26=172 т*м

База наружной ветви. Требуемая площадь плиты

172/0.085=2023.53 см2

R_B — расчётное сопротивление бетона на сжатие

По конструктивным соображениям свес плиты с₂ должен быть не менее 4см.

Тогда 39.6+2·4=47.6

принимаем B= 50 см;

= 2023.529/50=40.47 см

Принимаем L= 45 см;

45·50=2250

Среднее напряжение в бетоне под плитой

172·1000/2250=76.44 кг/см2