Симплекс-метод решения задачи линейного программирования
Рассмотрим каноническую ЗЛП
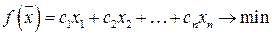 , (5.1)
, (5.1)
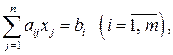 (5.2)
(5.2)
где 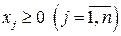 . Будем предполагать, что
. Будем предполагать, что 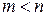 , система уравнений (5.2) совместна и имеет бесконечное множество решений.
, система уравнений (5.2) совместна и имеет бесконечное множество решений.
Для начала решения ЗЛП по симплекс-методу требуется, чтобы система ограничений (5.2) была приведена к допустимому виду (см. §4 ). Это означает, что какие-то 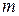 переменных выражены через остальные
переменных выражены через остальные 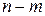 переменных, причем свободные члены в полученной системе неотрицательны. Пусть для определенности система ограничений имеет следующий допустимый вид
переменных, причем свободные члены в полученной системе неотрицательны. Пусть для определенности система ограничений имеет следующий допустимый вид
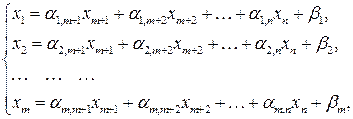 (5.3)
(5.3)
где 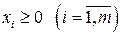 (базисные переменные) выражены через
(базисные переменные) выражены через 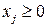
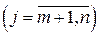 (свободные переменные), причем
(свободные переменные), причем 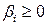
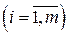 .
.
Так как переменные 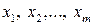 выражены через
выражены через 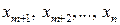 , то соответствующим образом необходимо изменить целевую функцию (5.1). Подставляя в (5.1) вместо
, то соответствующим образом необходимо изменить целевую функцию (5.1). Подставляя в (5.1) вместо 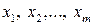 выражения, определяемые правыми частями системы (5.3), получим следующий вид целевой функции:
выражения, определяемые правыми частями системы (5.3), получим следующий вид целевой функции:
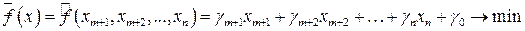 (5.4)
(5.4)
(целевая функция зависит от свободных переменных 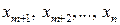 ).
).
Обозначим через 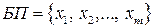 множество базисных переменных, через
множество базисных переменных, через 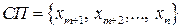 множество свободных переменных. Построим начальное опорное (базисное) решение системы ЗЛП (5.3) – (5.4), положив значения свободных переменных
множество свободных переменных. Построим начальное опорное (базисное) решение системы ЗЛП (5.3) – (5.4), положив значения свободных переменных 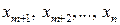 равными нулю:
равными нулю:
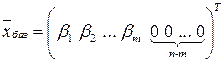 . (5.5)
. (5.5)
Значение целевой функции на базисном решении (5.5):
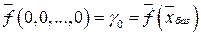 .
.
Возникает вопрос: можно ли уменьшить значение целевой функции? При решении ЗЛП симплекс-методом возникают три случая.
Случай 1. Предположим, что в целевой функции (5.4) ЗЛП допустимого вида все коэффициенты 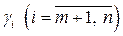 при свободных переменных неотрицательны. Заметим, что при любом допустимом решении
при свободных переменных неотрицательны. Заметим, что при любом допустимом решении
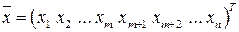 ,
,
являющимся решением системы (5.3), значение целевой функции (5.4) не меньше, чем значение целевой функции на базисном решении (5.5):
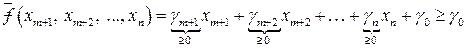 .
.
Таким образом, наименьшее значение целевой функции (5.4) достигается на базисном решении (5.5) и равно 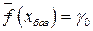 . Получаем теорему.
. Получаем теорему.
Теорема 5.1 (случай оптимальности базисного решения ЗЛП). Если в целевой функции (5.4) ЗЛП допустимого вида все коэффициенты 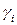
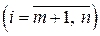 при свободных переменных
при свободных переменных 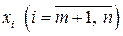 неотрицательны, то базисное решение (5.5) является оптимальным,
неотрицательны, то базисное решение (5.5) является оптимальным, 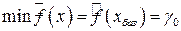 .
.
Пример 5.1. Найти оптимальное решениеЗЛП допустимого вида
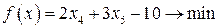 ,
, 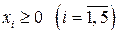 ,
,
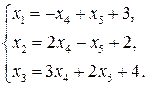
Решение. В данном случае 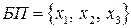 ,
, 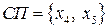 , базисное решение
, базисное решение 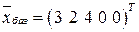 . В целевой функции
. В целевой функции 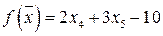 все коэффициенты при свободных переменных
все коэффициенты при свободных переменных 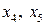 положительны (
положительны ( 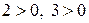 ). Согласно теореме 5.1 базисное решение
). Согласно теореме 5.1 базисное решение 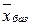 , полученное при нулевых значениях свободных переменных (
, полученное при нулевых значениях свободных переменных ( 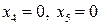 ), является оптимальным, причем
), является оптимальным, причем 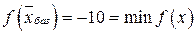 . Итак,
. Итак,
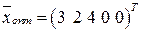 ,
, 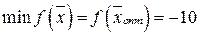 .
.
Случай 2. Предположим, что в целевой функции (5.4) ЗЛП допустимого вида среди коэффициентов 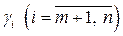 при свободных переменных существует отрицательный коэффициент, а в системе ограничений (5.3) все коэффициенты при этой же свободной переменной неотрицательны. Пусть для определенности при свободной переменной
при свободных переменных существует отрицательный коэффициент, а в системе ограничений (5.3) все коэффициенты при этой же свободной переменной неотрицательны. Пусть для определенности при свободной переменной 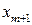 в целевой функции коэффициент
в целевой функции коэффициент 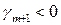 , а в системе ограничений (5.3):
, а в системе ограничений (5.3):
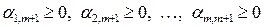 .
.
Построим допустимое решение 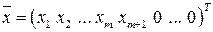 ,
, 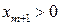 ,
,
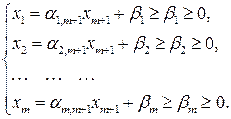 (5.6)
(5.6)
На этом допустимом решении значение целевой функции имеет вид
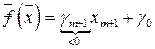 .
.
Заметим, что с неограниченным увеличением значения свободной переменной 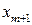 (
( 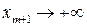 ) целевая функция
) целевая функция 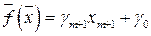 неограниченно уменьшается (
неограниченно уменьшается ( 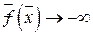 ). В данном случае задача не имеет оптимального решения (целевая функция не имеет наименьшего значения).
). В данном случае задача не имеет оптимального решения (целевая функция не имеет наименьшего значения).
Теорема 5.2 (случай отсутствия оптимального решения ЗЛП). Если в целевой функции (5.4) ЗЛП допустимого вида среди коэффициентов 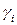
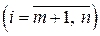 при свободных переменных существует отрицательный коэффициент, а в системе ограничений (5.3) все коэффициенты при этой же свободной переменной неотрицательны, то ЗЛП не имеет оптимального решения в силу неограниченности целевой функции этой задачи.
при свободных переменных существует отрицательный коэффициент, а в системе ограничений (5.3) все коэффициенты при этой же свободной переменной неотрицательны, то ЗЛП не имеет оптимального решения в силу неограниченности целевой функции этой задачи.
Пример 5.2. Доказать, чтоЗЛП не имеет оптимального решения
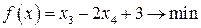 ,
, 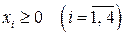 ,
,
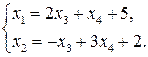
Решение. В данном случае 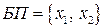 ,
, 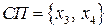 , базисное решение
, базисное решение 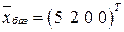 . В целевой функции
. В целевой функции 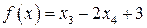 при свободной переменной
при свободной переменной 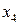 отрицательный коэффициент (
отрицательный коэффициент ( 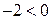 ), а в системе ограничений при этой же переменной все неотрицательные коэффициенты (
), а в системе ограничений при этой же переменной все неотрицательные коэффициенты ( 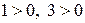 . Согласно теореме 5.2 ЗЛП не имеет оптимального решения.
. Согласно теореме 5.2 ЗЛП не имеет оптимального решения.
Случай 3. Пусть в целевой функции (5.4) ЗЛП допустимого вида среди коэффициентов 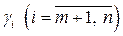 при свободных переменных существует отрицательный коэффициент (пусть для определенности
при свободных переменных существует отрицательный коэффициент (пусть для определенности 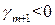 ) и в системе ограничений (5.3) при этой же свободной переменной также существует по крайней мере один отрицательный коэффициент.
) и в системе ограничений (5.3) при этой же свободной переменной также существует по крайней мере один отрицательный коэффициент.
Возникают два случая.
Случай 3.1. Пусть в системе ограничений (5.3) среди коэффициентов 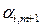
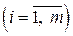 только один отрицательный. Предположим для определенности, что
только один отрицательный. Предположим для определенности, что 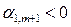 . Построим допустимое решение
. Построим допустимое решение
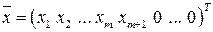 ,
,
где 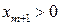 и переменные
и переменные 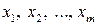 удовлетворяют системе (5.6).
удовлетворяют системе (5.6).
На этом допустимом решении значение целевой функции равно
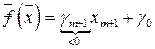 .
.
Уменьшение целевой функции можно достичь за счет увеличения значения свободной переменной 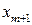 . Так как
. Так как 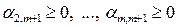 , то при увеличении значения свободной переменной
, то при увеличении значения свободной переменной 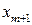 значения базисных переменных
значения базисных переменных 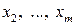 увеличиваются. Заметим, что увеличение значения свободной переменной
увеличиваются. Заметим, что увеличение значения свободной переменной 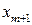 приводит к уменьшению значения базисной переменной
приводит к уменьшению значения базисной переменной  (
( 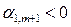 ), и при
), и при
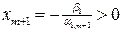
базисная переменная  обратится в нуль:
обратится в нуль:
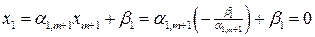 .
.
Обращение в нуль базисной переменной  при
при 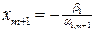 означает, что необходимо изменить базис переменных. А именно, переменную
означает, что необходимо изменить базис переменных. А именно, переменную  вывести из базиса переменных, а переменную
вывести из базиса переменных, а переменную 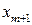 ввести в базис (обозначаем это так
ввести в базис (обозначаем это так 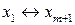 ). При этом число
). При этом число 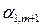 будем называть разрешающим элементом.
будем называть разрешающим элементом.
Случай 3.2. Пусть в системе ограничений (5.3) среди коэффициентов 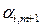
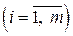 существуют по крайней мере два отрицательных. Пусть для определенности
существуют по крайней мере два отрицательных. Пусть для определенности 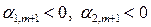 (при этом
(при этом 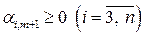 ).
).
Построим допустимое решение 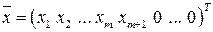 , где
, где 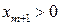 и
и 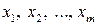 определяются из системы
определяются из системы
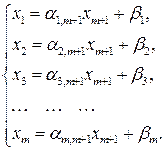
На этом допустимом решении значение целевой функции равно
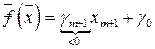 .
.
Так как 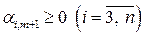 , то при увеличении значения свободной переменной
, то при увеличении значения свободной переменной 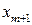 значения базисных переменных
значения базисных переменных 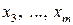 увеличиваются. Увеличение значения свободной переменной
увеличиваются. Увеличение значения свободной переменной 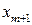 приводит к уменьшению значений базисных переменных
приводит к уменьшению значений базисных переменных 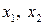 (так как
(так как 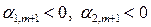 ). Составим вспомогательное число
). Составим вспомогательное число
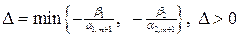 .
.
При увеличении значения свободной переменной 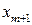 от 0 до
от 0 до 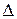 обязательно какая-то из базисных переменных
обязательно какая-то из базисных переменных 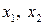 обратится в нуль. Предположим для определенности, что
обратится в нуль. Предположим для определенности, что 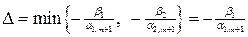 . Тогда при значении
. Тогда при значении 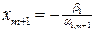 базисная переменная
базисная переменная  обратится в нуль. Как и в случае 3.1, это означает, что происходит смена базиса переменных:
обратится в нуль. Как и в случае 3.1, это означает, что происходит смена базиса переменных:  выходит из базиса переменных, а
выходит из базиса переменных, а 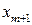 входит в базис (
входит в базис ( 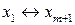 ). При этом, как и в случае 3.1, число
). При этом, как и в случае 3.1, число 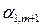 называют разрешающим элементом.
называют разрешающим элементом.
Обобщая сказанное в случае 3, необходимо переменную  вывести из базиса переменных, а
вывести из базиса переменных, а 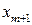 ввести в базис переменных. Для этого необходимо из системы ограничений (5.3) выразить переменную
ввести в базис переменных. Для этого необходимо из системы ограничений (5.3) выразить переменную 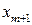 через переменную
через переменную  . Получим новую систему ограничений
. Получим новую систему ограничений
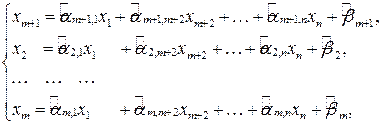 (5.7)
(5.7)
где обязательно 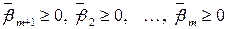 . При этом соответствующим образом изменится и целевая функция
. При этом соответствующим образом изменится и целевая функция
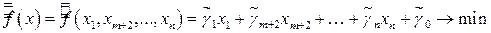 , (5.8)
, (5.8)
причем 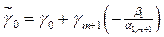 .
.
Получили новую ЗЛП допустимого вида с системой ограничений (5.7) и целевой функцией (5.8). В этой задаче 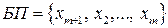 ,
, 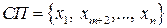 . Составим базисное решение, положив нулевыми значения свободных переменных:
. Составим базисное решение, положив нулевыми значения свободных переменных:
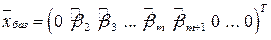 .
.
Заметим, что значение целевой функции на базисном решении 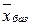
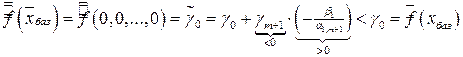 ,
,
то есть в результате смены базиса переменных значение целевой функции уменьшилось на значение 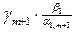 .
.
Популярное:

