Экономическая интерпретация решения
Задачи линейного программирования
В этом параграфе рассмотрим экономическую интерпретацию решений взаимно двойственных задач и основных теорем теории двойственности.
Рассмотрим математическую модель задачи об оптимальном использовании ресурсов:
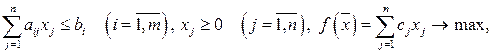 (10.1)
(10.1)
где 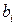 – запас
– запас 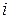 -го сырья (
-го сырья ( 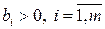 ),
), 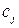 – стоимость одной единицы
– стоимость одной единицы 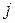 -го продукта (
-го продукта ( 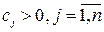 ),
), 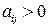 – норма расхода
– норма расхода 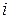 -го сырья на производство одной единицы
-го сырья на производство одной единицы 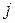 -го продукта,
-го продукта, 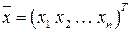 – вектор-столбец управляющих переменных,
– вектор-столбец управляющих переменных, 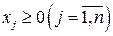 – количество единиц
– количество единиц 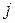 -го продукта.
-го продукта.
Экономический смысл задачи (10.1): сколько и какой продукции 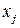 (
( 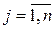 ) нужно произвести, чтобы при заданных стоимостях единицы продукции
) нужно произвести, чтобы при заданных стоимостях единицы продукции 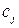 (
( 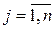 ), объемах имеющихся ресурсов
), объемах имеющихся ресурсов 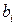 (
( 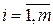 ) и нормах их расходов
) и нормах их расходов 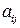 максимизировать выпуск продукции в стоимостном выражении.
максимизировать выпуск продукции в стоимостном выражении.
Оптимальный план ЗЛП (10.1) состоит из управляющих 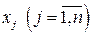 и
и
балансовых переменных 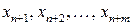 . Если управляющая переменная
. Если управляющая переменная
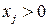 (
( 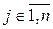 ) в оптимальном плане, то соответствующий ей продукт производится в объеме
) в оптимальном плане, то соответствующий ей продукт производится в объеме 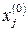 единиц. Если управляющая переменная
единиц. Если управляющая переменная 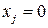 (
( 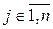 ) в оптимальном плане, то соответствующий ей продукт не производится, его производство не выгодно предприятию.
) в оптимальном плане, то соответствующий ей продукт не производится, его производство не выгодно предприятию.
Если в оптимальном плане задачи (10.1) содержится балансовая переменная 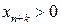 (
( 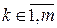 ), то соответствующий ей
), то соответствующий ей 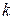 -ый ресурс является недефицитным, а значение
-ый ресурс является недефицитным, а значение 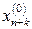 показывает величину недоиспользованного ресурса. Если же в оптимальном плане задачи (10.1) балансовая переменная
показывает величину недоиспользованного ресурса. Если же в оптимальном плане задачи (10.1) балансовая переменная 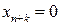 (
( 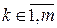 ), то соответствующий ей ресурс является дефицитным (полностью потребляется в производстве).
), то соответствующий ей ресурс является дефицитным (полностью потребляется в производстве).
Рассмотрим двойственную задачу к задаче (10.1):
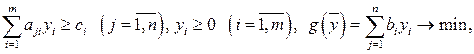 (10.2)
(10.2)
где управляющие переменные 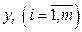 выполняют роль двойственных оценок ресурсов прямой задачи (10.1).
выполняют роль двойственных оценок ресурсов прямой задачи (10.1).
Сформулируем экономический смысл двойственной задачи (10.2). Какова должна быть оценка 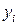 единицы каждого из ресурсов (
единицы каждого из ресурсов ( 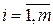 ), чтобы при заданных запасах
), чтобы при заданных запасах 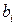 (
( 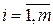 ), ценах единицы продукции
), ценах единицы продукции 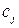 (
( 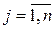 ) и нормах расходов
) и нормах расходов 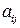 минимизировать общую оценку затрат на все ресурсы.
минимизировать общую оценку затрат на все ресурсы.
Если в оптимальный план задачи (10.2) оценка 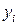 вошла с положительным значением (
вошла с положительным значением ( 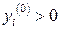 ), то соответствующий
), то соответствующий 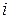 -ый ресурс является дефицитным. Если же в оптимальном плане задачи (10.2) оценка
-ый ресурс является дефицитным. Если же в оптимальном плане задачи (10.2) оценка 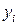 равна нулю, то соответствующий
равна нулю, то соответствующий 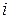 -ый ресурс является недефицитным.
-ый ресурс является недефицитным.
Пример 10.1 [17].На основании информации, приведенной в таблице 10.1, составить оптимальный план производства, максимизирующий объем прибыли. Выполнить экономическую интерпретацию решения прямой задачи и соответствующей двойственной задачи. Выделить дефицитные и недефицитные ресурсы.
Табл. 10.1.
|
Ресурсы
| Затраты ресурсов на единицу продукции
|
Наличие ресурсов
|
А (  ) )
| Б ( 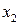 ) )
|
| Труд
|
|
|
|
| Сырье
|
|
|
|
| Оборудование
|
|
|
|
| Прибыль на единицу продукции
|
|
|
|
Экономико-математическая модель задачи имеет вид
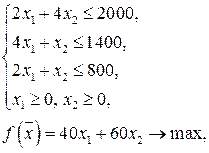
где 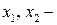 количество продуктов А и Б соответственно.
количество продуктов А и Б соответственно.
В результате решения ЗЛП с естественным базисом из балансовых переменных 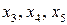 получена результирующая таблица 10.2.
получена результирующая таблица 10.2.
Табл. 10.2
Из табл. 10.2 следует, что ЗЛП имеет следующий оптимальный план
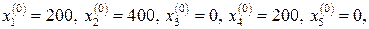
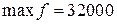 .
.
Так как в оптимальный план обе управляющие переменные  вошли с положительными значениями, то предприятию выгодно производить оба вида продукта в объемах
вошли с положительными значениями, то предприятию выгодно производить оба вида продукта в объемах 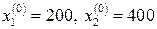 единиц. Балансовая переменная
единиц. Балансовая переменная 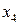 в оптимальный план вошла с положительным значением, что означает, что соответствующий ресурс (сырье) является недефицитным. Труд и оборудование являются, наоборот, дефицитными ресурсами.
в оптимальный план вошла с положительным значением, что означает, что соответствующий ресурс (сырье) является недефицитным. Труд и оборудование являются, наоборот, дефицитными ресурсами.
Составив и решив соответствующую двойственную задачу, получим следующее оптимальное решение

Так как 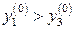 , то ресурс труд более дефицитен, чем ресурс оборудование. Наиболее выгодно увеличение объемов ресурсов труда.
, то ресурс труд более дефицитен, чем ресурс оборудование. Наиболее выгодно увеличение объемов ресурсов труда.
Замечание 10.1. Если прямая задача (10.1) решена симплекс-методом с естественным базисом из переменных 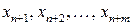 , то решение соответствующей двойственной задачи может быть найдено по формуле
, то решение соответствующей двойственной задачи может быть найдено по формуле
 , (10.3)
, (10.3)
где 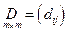 – матрица, обратная к матрице
– матрица, обратная к матрице 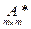 , являющейся матрицей коэффициентов базисных переменных системы ограничений прямой задачи (10.1) (то есть тех переменных, которые в результате решения симплекс-методом вошли в оптимальный план),
, являющейся матрицей коэффициентов базисных переменных системы ограничений прямой задачи (10.1) (то есть тех переменных, которые в результате решения симплекс-методом вошли в оптимальный план), 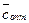 – вектор-столбец размера
– вектор-столбец размера 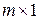 коэффициентов при базисных переменных целевой функции
коэффициентов при базисных переменных целевой функции 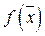 в оптимальном решении прямой задачи.
в оптимальном решении прямой задачи.
В примере 10.1 основная матрица канонической ЗЛП имеет вид
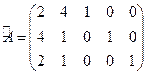 .
.
В оптимальный план прямой задачи вошли переменные 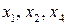 (см. табл. 10.2). Значит, матрица
(см. табл. 10.2). Значит, матрица 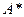 составлена из первого, второго и четвертого столбцов матрицы
составлена из первого, второго и четвертого столбцов матрицы 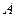 . Тогда имеем:
. Тогда имеем:
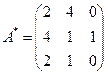 ,
, 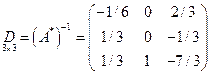 .
.
Заметим, что матрицу 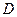 можно найти непосредственно из результирующей симплекс-таблицы. Для этого достаточно выписать матрицу коэффициентов при дополнительных переменных.
можно найти непосредственно из результирующей симплекс-таблицы. Для этого достаточно выписать матрицу коэффициентов при дополнительных переменных.
Вектор-столбец 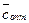 имеет вид
имеет вид 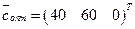 .
.
По формуле (10.3) находим оптимальное решение двойственной ЗЛП:
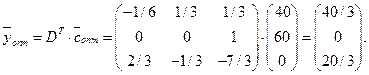
Сформулируем экономические интерпретации основных теорем теории двойственности.
Экономическая интерпретация основного неравенства теории двойственности: для любого допустимого плана производства 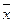 и любого допустимого вектора оценок ресурсов
и любого допустимого вектора оценок ресурсов 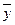 общая созданная стоимость не превосходит суммарной оценки ресурсов (
общая созданная стоимость не превосходит суммарной оценки ресурсов ( 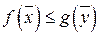 ).
).
Экономическая интерпретация первой теоремы двойственности: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов, причем цена продукта, полученного в результате реализации оптимального плана, совпадает с суммарной оценкой ресурсов ( 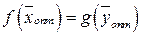 ). Для всех других планов
). Для всех других планов 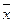 и оценок ресурсов
и оценок ресурсов 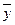 обеих задач цена произведенной продукции всегда меньше суммарной оценки затраченных ресурсов.
обеих задач цена произведенной продукции всегда меньше суммарной оценки затраченных ресурсов.
Двойственные оценки ресурсов выступают как инструмент балансирования затрат и результатов экономической системы. Они гарантируют рентабельность оптимального плана, то есть равенство общей оценки продукции и ресурсов обусловливает убыточность всякого другого плана, отличного от оптимального плана. Величина 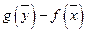 характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных оценок ресурсов. При оптимальной производственной программе и оптимальном векторе оценок ресурсов производственные потери равны нулю, то есть предприятию безразлично, производить ли продукцию по оптимальному плану и получать максимальную прибыль, или продать ресурсы по оптимальным ценам и выручить от продажи минимальные затраты на ресурсы.
характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных оценок ресурсов. При оптимальной производственной программе и оптимальном векторе оценок ресурсов производственные потери равны нулю, то есть предприятию безразлично, производить ли продукцию по оптимальному плану и получать максимальную прибыль, или продать ресурсы по оптимальным ценам и выручить от продажи минимальные затраты на ресурсы.
Рассмотрим экономический смысл второй теоремы двойственности.Из второй теоремы двойственности и условий дополняющей нежесткости
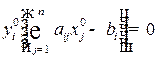 (
( 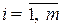 ) (10.4)
) (10.4)
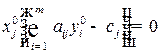 (
( 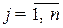 ) (10.5)
) (10.5)
следуют требования на оптимальную производственную программу 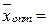
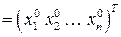 и оптимальный вектор оценок
и оптимальный вектор оценок 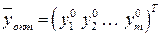 .
.
Условия (10.4) можно интерпретировать так: если по некоторому оптимальному плану 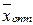 производства расход ресурса
производства расход ресурса 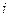 -го вида строго меньше запаса
-го вида строго меньше запаса 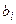 (
( 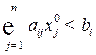 ), то в оптимальном плане
), то в оптимальном плане 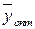 соответствующая оценка
соответствующая оценка 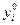 единицы этого ресурса равна нулю; если же в некотором оптимальном плане оценок величина
единицы этого ресурса равна нулю; если же в некотором оптимальном плане оценок величина 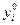 положительна, то при оптимальной производственной программе этот ресурс используется полностью (расход этого ресурса равен его запасу
положительна, то при оптимальной производственной программе этот ресурс используется полностью (расход этого ресурса равен его запасу 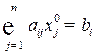 , ресурс является дефицитным). Из условий (10.5) следует, что если
, ресурс является дефицитным). Из условий (10.5) следует, что если 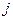 -й вид продукции вошел в оптимальный план (
-й вид продукции вошел в оптимальный план ( 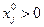 ), то он в двойственных оценках не убыточен (
), то он в двойственных оценках не убыточен ( 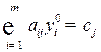 ). Если же
). Если же 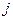 -й вид продукции убыточен, то он не войдет в оптимальный план, не будет выпускаться (
-й вид продукции убыточен, то он не войдет в оптимальный план, не будет выпускаться ( 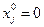 ).
).
Популярное:

