Общая постановка задачи линейного программирования
Геометрический метод решения
Рис. 3.1.
Пусть, например, полуплоскость 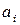 определяется неравенством
определяется неравенством 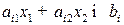 . Для построения полуплоскости
. Для построения полуплоскости 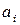 (
( 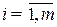 ) достаточно подставить в соответствующее неравенство координаты любой точки (например, (0, 0)) и проверить истинность полученного неравенства. Если неравенство истинное, то необходимо заштриховать полуплоскость, содержащую данную точку. В случае, если неравенство ложное, то заштриховать полуплоскость, не содержащую данную точку.
) достаточно подставить в соответствующее неравенство координаты любой точки (например, (0, 0)) и проверить истинность полученного неравенства. Если неравенство истинное, то необходимо заштриховать полуплоскость, содержащую данную точку. В случае, если неравенство ложное, то заштриховать полуплоскость, не содержащую данную точку.
Условия неотрицательности управляющих переменных  ,
, 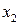 определяют полуплоскость с граничными прямыми
определяют полуплоскость с граничными прямыми 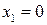 ,
, 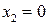 (первую координатную четверть). Так как система ограничений совместна, то полуплоскости имеют общую область. Пересечение полуплоскостей является выпуклым множеством и представляет собой совокупность точек, координаты которых составляют допустимые решения.
(первую координатную четверть). Так как система ограничений совместна, то полуплоскости имеют общую область. Пересечение полуплоскостей является выпуклым множеством и представляет собой совокупность точек, координаты которых составляют допустимые решения.
2) Построим градиент целевой функции 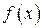 (в данном случае геометрический вектор):
(в данном случае геометрический вектор):
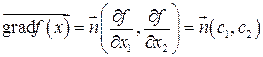
с началом в точке 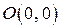 и концом в точке
и концом в точке 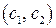 , показывающий направление наибольшего возрастания целевой функции
, показывающий направление наибольшего возрастания целевой функции 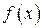 .
.
3) Построим линию уровня целевой функции 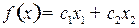 . Эта линия есть прямая
. Эта линия есть прямая 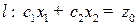 (при
(при 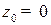 получаем линию нулевого уровня
получаем линию нулевого уровня 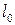 , см. рис. 3.1), и она перпендикулярна градиенту
, см. рис. 3.1), и она перпендикулярна градиенту 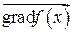 . Как правило, значение
. Как правило, значение 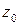 целесообразно выбирать таким образом, чтобы соответствующая линия уровня имела с множеством допустимых решений по крайней мере две общие точки.
целесообразно выбирать таким образом, чтобы соответствующая линия уровня имела с множеством допустимых решений по крайней мере две общие точки.
4) При решении задачи на максимум функции 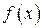 следует перемещать линию уровня
следует перемещать линию уровня 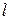 в направлении градиента до тех пор, пока у нее не окажется всего одна общая точка с множеством допустимых решений. Эта точка, определяющая единственное решение ЗЛП, будет точкой экстремума (максимума). При решении задачи на минимум функции
в направлении градиента до тех пор, пока у нее не окажется всего одна общая точка с множеством допустимых решений. Эта точка, определяющая единственное решение ЗЛП, будет точкой экстремума (максимума). При решении задачи на минимум функции 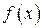 следует перемещать линию уровня в направлении, противоположном направлению градиента до тех пор, пока у нее не окажется всего одна общая точка с множеством допустимых решений. Эта точка, определяющая единственное решение ЗЛП, будет точкой экстремума (минимума).
следует перемещать линию уровня в направлении, противоположном направлению градиента до тех пор, пока у нее не окажется всего одна общая точка с множеством допустимых решений. Эта точка, определяющая единственное решение ЗЛП, будет точкой экстремума (минимума).
5) Найти координаты вершины многоугольника, являющейся точкой экстремума. Для этого нужно решить систему уравнений тех прямых, пересечением которых является данная вершина.
6) Вычислить значение целевой функции 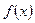 в полученной вершине.
в полученной вершине.
Замечание 3.1. Если при движении вдоль градиента 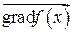 линия уровня не покидает множество допустимых решений, то это множество является неограниченным в направлении оптимизации. В этом случае условно полагают, что
линия уровня не покидает множество допустимых решений, то это множество является неограниченным в направлении оптимизации. В этом случае условно полагают, что 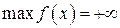 или
или 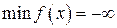 .
.
Замечание 3.2. ЗЛП не будет иметь решений, если множество допустимых решений является пустым множеством. Это означает, что система ограничений имеет противоречивые неравенства, и на координатной плоскости нет ни одной точки, удовлетворяющей всем ограничениям сразу.
Замечание 3.3. При решении ЗЛП графическим методом может встретиться случай, когда линия уровня параллельна одной из сторон выпуклого многоугольника допустимых решений, причем эта сторона расположена в направлении оптимизации. Тогда оптимальное значение целевой функции достигается в двух угловых точках (вершинах) области допустимых решений, а, следовательно, и во всех точках отрезка, соединяющего эти вершины, то есть ЗЛП имеет бесконечное множество решений (альтернативный оптимум).
Пример 3.1. Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в таблице:
| Исходный
продукт
| Расход исходных продуктов
на 1 кг мороженого
| Запас, кг
|
| Сливочное
| Шоколадное
|
| Молоко
| 0, 8
| 0, 5
|
|
| Наполнители
| 0, 4
| 0, 8
|
|
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более, чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 руб., шоколадного – 14 руб. Какое количество мороженого каждого вида должна производить
фирма, чтобы доход от реализации продукции был максимальным? [1; 2].
Решение. Обозначим управляющие переменные: 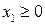 – суточный объем выпуска сливочного мороженого, кг;
– суточный объем выпуска сливочного мороженого, кг; 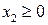 – суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Целевая функция будет иметь вид
– суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи. Целевая функция будет иметь вид 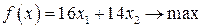 .
.
Составим неравенства для ресурсных ограничений. Ограничение по молоку имеет вид: 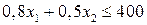 ; по наполнителям:
; по наполнителям: 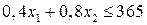 . Составим неравенства для рыночных ограничений по спросу. Разница в суточном спросе на 2 вида мороженого составляет
. Составим неравенства для рыночных ограничений по спросу. Разница в суточном спросе на 2 вида мороженого составляет 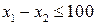 . Ограничение на суточный спрос шоколадного мороженого
. Ограничение на суточный спрос шоколадного мороженого 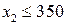 .
.
Тогда математическая модель задачи будет иметь вид
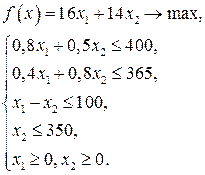
Далее решим задачу графическим методом.
1) Построим множество допустимых решений. Неравенство 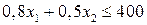 определяет полуплоскость, расположенную левее и ниже прямой
определяет полуплоскость, расположенную левее и ниже прямой 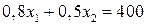 , то есть прямой
, то есть прямой 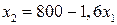 . Неравенство
. Неравенство 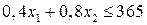 определяет полуплоскость, расположенную левее и ниже прямой
определяет полуплоскость, расположенную левее и ниже прямой 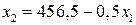 . Ограничение
. Ограничение 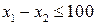 определяет полуплоскость, расположенную левее и ниже прямой
определяет полуплоскость, расположенную левее и ниже прямой 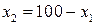 . Ограничение
. Ограничение 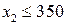 определяет полуплоскость, расположенную левее прямой
определяет полуплоскость, расположенную левее прямой 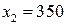 , ограничения
, ограничения 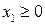 ,
, 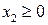 определяют первую координатную четверть. Множество допустимых решений ЗЛП не пусто. Обозначим вершины многоугольника решений:
определяют первую координатную четверть. Множество допустимых решений ЗЛП не пусто. Обозначим вершины многоугольника решений:  (рис. 3.2).
(рис. 3.2).
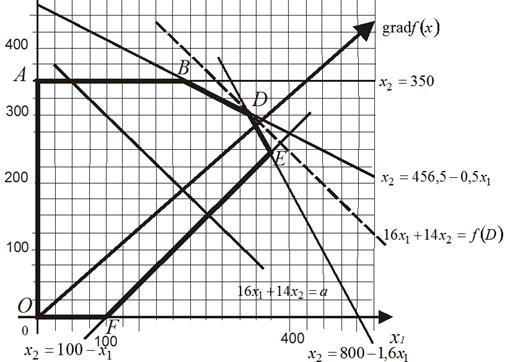 Рис. 3.2.
Рис. 3.2.
|
2) Построим градиент целевой функции 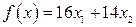 :
:
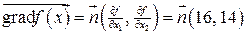 .
.
3) Построим линию уровня 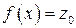 целевой функции
целевой функции 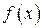 :
: 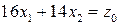 . Линия уровня перпендикулярна вектору
. Линия уровня перпендикулярна вектору 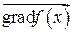 .
.
4) Перемещая прямую 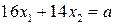 по направлению
по направлению 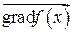 параллельно самой себе, найдем предельную точку, в которой целевая функция
параллельно самой себе, найдем предельную точку, в которой целевая функция 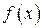 покинет область допустимых решений (пунктирная линия на рис. 3.2). Предельная точка многоугольника
покинет область допустимых решений (пунктирная линия на рис. 3.2). Предельная точка многоугольника 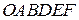 – точка
– точка 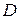 .
.
5) Найдем координаты точки 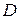 как точки пересечения прямых
как точки пересечения прямых 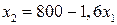 и
и 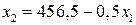 :
:
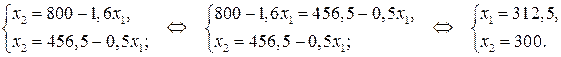
Следовательно, точка 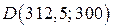 .
.
6) Найдем значение целевой функции в точке 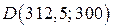 :
:
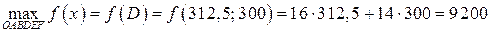 рублей.
рублей.
При помощи симплекс-таблиц
В предыдущем параграфе был рассмотрен симплекс-метод решения ЗЛП. Алгоритм симплекс-метода основан на последовательном улучшении (минимизации) целевой функции и построении базисного (опорного) решения (плана). Оптимальное решение достигается последовательным улучшением начального опорного плана за определенное число этапов (итераций). Переход к следующему опорному решению проводится на основе метода Жордана–Гаусса для систем линейных алгебраических уравнений. Направление перехода от одного базисного решения к другому выбирается на основе двух теорем (принципов оптимальности ЗЛП, теорема 5.1, теорема 5.2). Полученный опорный план на каждом шаге симплекс-метода проверяется на оптимальность. Процесс оканчивается за конечное число шагов. Причем на последнем шаге либо получается оптимальный опорный план и соответствующее ему оптимальное значение целевой функции (теорема 5.1), либо выявляется неразрешимость задачи (конечного оптимума нет).
Оказывается, что все вычисления по симплекс-методу удобно производить в так называемых симплекс-таблицах.
Как и в предыдущем параграфе, рассмотрим ЗЛП в допустимом виде
 (6.1)
(6.1)
где базисные переменные 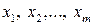 выражены через свободные переменные
выражены через свободные переменные 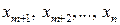 , причем
, причем  . Целевая функция имеет вид
. Целевая функция имеет вид
 . (6.2)
. (6.2)
Приведем ЗЛП (6.1) – (6.2) к каноническому виду
 (6.3)
(6.3)
 . (6.4)
. (6.4)
Рассмотрим алгоритм решения ЗЛП, используя результаты предыдущего параграфа (теоремы 5.1, 5.2). В целях наглядности рассмотрим ЗЛП
 (6.3′ )
(6.3′ )
 , (6.4′ )
, (6.4′ )
в которой три базисные переменные 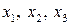 и три свободные переменные
и три свободные переменные  , причем
, причем  .
.
Составим начальную симплекс-таблицу (табл. 6.1). В столбце БП выписываем базисные переменные 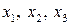 , в столбце СЧ – коэффициенты
, в столбце СЧ – коэффициенты  в правой части системы ограничений (6.3′ ). В следующих столбцах выписываются коэффициенты при переменных в левой части системы (6.3′ ). Последняя строка таблицы составляется по коэффициентам при переменных в целевой функции (6.4′ ).
в правой части системы ограничений (6.3′ ). В следующих столбцах выписываются коэффициенты при переменных в левой части системы (6.3′ ). Последняя строка таблицы составляется по коэффициентам при переменных в целевой функции (6.4′ ).
Табл. 6.1
По табл. 6.1 построим начальный:  (значения свободных переменных
(значения свободных переменных  равны нулю); соответственно значение целевой функции на базисном решении
равны нулю); соответственно значение целевой функции на базисном решении 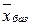 равно
равно  .
.
Проверим построенное базисное решение 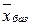 на оптимальность. Возникают три случая:
на оптимальность. Возникают три случая:
Случай 1. Пусть в последней строке симплекс-таблицы все коэффициенты при свободных переменных  неположительны:
неположительны:
 .
.
Это условие равносильно тому, что 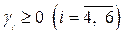 . Тогда согласно теореме 5.1 базисное решение
. Тогда согласно теореме 5.1 базисное решение  является оптимальным:
является оптимальным:
 ,
,  .
.
Случай 2. Пусть в последней строке симплекс-таблицы среди коэффициентов  есть положительный коэффициент (предположим для определенности:
есть положительный коэффициент (предположим для определенности:  ), а все коэффициенты при соответствующей свободной переменной отрицательные (в нашем случае все коэффициенты
), а все коэффициенты при соответствующей свободной переменной отрицательные (в нашем случае все коэффициенты  ,
,  ,
,  при соответствующей свободной переменной
при соответствующей свободной переменной 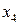 отрицательны). Это условие равносильно тому, что
отрицательны). Это условие равносильно тому, что
 ,
, 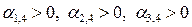 .
.
Тогда согласно теореме 5.2, ЗЛП не имеет оптимального решения.
Случай 3. Пусть в последней строке симплекс-таблицы среди коэффициентов  есть положительный, и при соответствующей свободной переменной в системе ограничений также имеется положительный коэффициент. Предположим для определенности, что
есть положительный, и при соответствующей свободной переменной в системе ограничений также имеется положительный коэффициент. Предположим для определенности, что  , и при соответствующей свободной переменной
, и при соответствующей свободной переменной 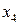 в системе ограничений среди
в системе ограничений среди  ,
,  ,
,  имеется положительный коэффициент. При этом столбец коэффициентов при переменной
имеется положительный коэффициент. При этом столбец коэффициентов при переменной 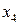 в таблице называется разрешающим столбцом (выделяем его в таблице вертикальной стрелкой
в таблице называется разрешающим столбцом (выделяем его в таблице вертикальной стрелкой  ). Согласно предыдущему параграфу, необходимо изменить базис переменных. Составим вспомогательное число
). Согласно предыдущему параграфу, необходимо изменить базис переменных. Составим вспомогательное число
 ,
,
где индекс 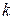 принимает те значения от 1 до 3, при которых
принимает те значения от 1 до 3, при которых  . Предположим для определенности, что
. Предположим для определенности, что  . Тогда число
. Тогда число  называется разрешающим элементом (выделен в табл. 6.2 в прямоугольник, строка коэффициентов при переменной
называется разрешающим элементом (выделен в табл. 6.2 в прямоугольник, строка коэффициентов при переменной  называется разрешающей строкой).
называется разрешающей строкой).
Табл. 6.2
Согласно симплекс-методу, необходимо изменить базис переменных: переменную  вывести из базиса, а
вывести из базиса, а 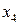 ввести в базис. Для этого составляется новая симплекс-таблица (табл. 6.3) по следующему правилу:
ввести в базис. Для этого составляется новая симплекс-таблица (табл. 6.3) по следующему правилу:
1) Базисными переменными являются  , свободными – переменные
, свободными – переменные 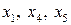 (переменная
(переменная 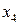 сменила переменную
сменила переменную  в базисе);
в базисе);
2) Разрешающая строка (в данном случае строка коэффициентов при переменной  ) делится на разрешающий элемент (в нашем случае на число
) делится на разрешающий элемент (в нашем случае на число  ). Полученная строка записывается в новую строку следующей таблицы, соответствующей новой базисной переменной;
). Полученная строка записывается в новую строку следующей таблицы, соответствующей новой базисной переменной;
3) В разрешающем столбце таблицы 6.2 (в столбце коэффициентов при 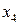 ) необходимо получить нули. Для этого применяем элементарные преобразования над строками таблицы 6.2. Полученные результаты записываем в соответствующие строки табл. 6.3.
) необходимо получить нули. Для этого применяем элементарные преобразования над строками таблицы 6.2. Полученные результаты записываем в соответствующие строки табл. 6.3.
Табл. 6.3
Покажем, что в табл. 6.3 коэффициенты  ,
,  ,
,  неотрицательны. Действительно,
неотрицательны. Действительно, 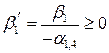 (так как по
(так как по 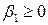 ,
, 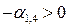 ).
).
Далее, если даже коэффициент  отрицательный, то в силу того, что
отрицательный, то в силу того, что 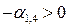 :
:
 .
.
Если же коэффициент  положительный, то в силу выбора разрешающего элемента имеем
положительный, то в силу выбора разрешающего элемента имеем
 .
.
Итак, в любом случае коэффициент  неотрицательный. Аналогично показывается, что коэффициент
неотрицательный. Аналогично показывается, что коэффициент  неотрицательный.
неотрицательный.
Это показывает, что вектор-столбец  , полученный при нулевых значениях свободных переменных, является допустимым решением ЗЛП.
, полученный при нулевых значениях свободных переменных, является допустимым решением ЗЛП.
Значение целевой функции на базисном решении 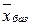 равно
равно
 .
.
Так как по условию 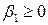 ,
, 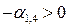 ,
,  , то
, то  , а значит,
, а значит,
 ,
,
то есть в процессе смены базиса целевая функция ЗЛП уменьшилась на значение  , что является оправданием шага симплекс-метода.
, что является оправданием шага симплекс-метода.
Пользуясь таблицей 6.3, далее необходимо вновь проверить базисное решение 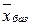 на оптимальность (проверить возможность возникновения одного из трех описанных случаев).
на оптимальность (проверить возможность возникновения одного из трех описанных случаев).
Пример 6.1. Решить ЗЛП при помощи симплекс-таблиц.

 ,
,

Решение. 1) Приведем ЗЛП к каноническому виду. Введем в систему ограничений балансовые переменные  . Так как
. Так как  , то введем функцию
, то введем функцию
 ,
,
сведя задачу к поиску минимума функции  :
:  .
.
Получили следующую ЗЛП канонического вида

 ,
,

2) Для полученной ЗЛП базис переменных  . Составим базисное решение
. Составим базисное решение  ,
,  . Получаем симплекс-таблицу (табл. 6.4).
. Получаем симплекс-таблицу (табл. 6.4).
Табл. 6.4
| БП
| СЧ
| 
| 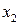
| 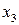
| 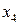
| 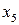
| 
| Преобразования
|

|
| 
|
| –1
|
|
|
|    
|
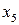
|
| –2
| –1
|
|
|
|
|
|

|
|
| –3
|
|
|
|
|
|
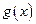
| – 5
|
| –3
|
|
|
|
|
|
Проверяем базисное решение  на оптимальность. В полученной табл. 6.4 в последней строке коэффициентов при переменных
на оптимальность. В полученной табл. 6.4 в последней строке коэффициентов при переменных 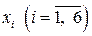 присутствует положительный коэффициент (
присутствует положительный коэффициент ( 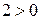 ). Столбец
). Столбец  является разрешающим (отмечаем
является разрешающим (отмечаем  ). Составляем число
). Составляем число
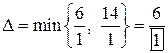 ,
,
откуда следует, что число 1 – знаменатель первой (наименьшей) дроби является разрешающим элементом (он выделен в табл. 6.4 в прямоугольнике, строка коэффициентов при переменной 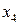 является разрешающей строкой). Производим смену базиса:
является разрешающей строкой). Производим смену базиса:  .
.
3) Составляем следующую симплекс-таблицу. Для этого делим 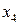 -строку табл. 6.4 на разрешающий элемент
-строку табл. 6.4 на разрешающий элемент  и при помощи элементарных преобразований обнуляем элементы, стоящие под разрешающим элементом. Получаем табл. 6.5.
и при помощи элементарных преобразований обнуляем элементы, стоящие под разрешающим элементом. Получаем табл. 6.5.
Табл. 6.5
| БП
| СЧ
| 
| 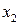
| 
| 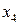
| 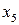
| 
| Преобразования
|

|
|
|
| – 1
|
|
|
| 
|
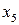
|
|
|
| – 1
|
|
|
| 
|
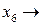
|
|
| – 5
| 
| – 1
|
|
|  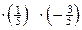
|
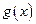
| – 17
|
| – 7
|
| – 2
|
|
|
|
Переменные  образуют базис переменных:
образуют базис переменных: 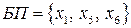 . Составим базисное решение
. Составим базисное решение 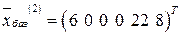 ,
,  . Как видно,
. Как видно,  , то есть в результате шага симплекс-метода целевая функция
, то есть в результате шага симплекс-метода целевая функция  уменьшила свое значение на 12.
уменьшила свое значение на 12.
4) Проверим базисное решение  на оптимальность. Как видно из табл. 6.5, разрешающим столбцом является
на оптимальность. Как видно из табл. 6.5, разрешающим столбцом является 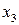 -столбец, разрешающим элементом – элемент 5. Происходит смена базиса:
-столбец, разрешающим элементом – элемент 5. Происходит смена базиса:  . В результате шага симплекс-метода получаем таблицу 6.6.
. В результате шага симплекс-метода получаем таблицу 6.6.
Табл. 6.6
Базисное решение  . При этом
. При этом 
 . Проверяя решение
. Проверяя решение 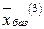 на оптимальность, замечаем, что в последней строке табл. 6.6, нет ни одного положительного числа. Согласно критерию оптимальности, базисное решение
на оптимальность, замечаем, что в последней строке табл. 6.6, нет ни одного положительного числа. Согласно критерию оптимальности, базисное решение 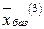 является оптимальным. Возвращаясь к исходной задаче, записываем ответ:
является оптимальным. Возвращаясь к исходной задаче, записываем ответ:
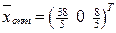 ,
, 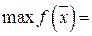
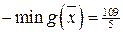 .
.
Табл. 7.1
| БП
| СЧ
| 
| 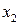
| 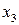
| 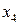
| 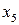
| 
| 
| Преобразования
|
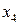
|
|
|
| – 1
|
|
|
|
|  
|

|
| 
|
| – 3
|
|
|
|
|   
|

|
| – 1
| – 4
|
|
| – 1
|
|
|
|
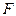
| 
| 
| 
| 
|
| 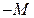
|
|
| 
|
Базисное решение имеет вид
 .
.
Проверим базисное решение  на оптимальность. В качестве разрешающего столбца выберем
на оптимальность. В качестве разрешающего столбца выберем  -столбец, так как при
-столбец, так как при  :
:  (остальные коэффициенты
(остальные коэффициенты  ,
,  ,
, 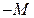 следует считать отрицательными). Разрешающий элемент в
следует считать отрицательными). Разрешающий элемент в  -столбце равен 2:
-столбце равен 2:
 .
.
На первом шаге симплекс-метода происходит смена базиса  с соответствующими преобразованиями в табл. 7.1. В результате получаем табл. 7.2.
с соответствующими преобразованиями в табл. 7.1. В результате получаем табл. 7.2.
Табл. 7.2
| БП
| СЧ
| 
| 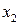
| 
| 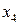
| 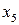
| 
| 
| Преобразования
|
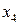
|
|
|
| 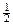
|
|
| 
|
|  
|

|
|
|
| 
|
|
| 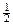
|
|  
|

|
|
| – 3
| 
|
| – 1
| 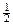
|
|  
|
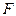
| 
|
| 
| 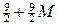
|
| 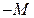
| 
|
| 
|
Базисное решение имеет вид
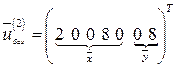 .
.
Популярное:

