В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
1) Построить интервальный ряд распределения; для каждого интервала подсчитать локальные, а также накопленные частоты; построить вариационный ряд.
Построить полигон и гистограмму;
Определить выборочную среднюю; а также низшую и высшую частные средние; моду и медиану; дисперсию и среднее квадратическое отклонение; коэффициент вариации;
2) Проверить при уровне значимости 0, 05 гипотезу о нормальном законе распределения соответствующего признака с помощью критериев согласия χ 2 ─ Пирсона и  ─ Смирнова; ─ Смирнова;
3) Найти точечные и интервальные оценки генеральной средней и среднего квадратического отклонения (при доверительной вероятности р = 0, 95);
4) Найти ошибки выборочных оценок;
5) Произвести анализ всех вычисленных статистических параметров.
13.1. На 60 сортоиспытательных участках определена следующая урожайность яровой пшеницы, ц/га:
23, 9; 18, 4; 23, 1; 16, 3; 21, 8; 17, 6; 17, 7; 19, 4; 19, 1; 18, 3; 23, 1; 21, 7; 18, 0; 19, 2; 19, 5; 19, 2; 18, 2; 20, 2; 25, 1; 19, 6; 24, 2; 22, 5; 23, 2; 16, 4; 21, 9; 21, 7; 19, 6; 19, 8; 20, 5; 20, 7; 21, 2; 25, 0; 21, 6; 21, 2; 20, 1; 20, 9; 20, 6; 18, 1; 19, 5; 20, 1; 25, 0; 21, 6; 20, 5; 20, 4; 20, 6; 21, 3; 25, 1; 21, 7; 21, 3; 20, 2; 22, 9; 23, 4; 22, 1; 17, 3; 20, 8; 22, 6; 19, 5; 21, 4; 19, 6; 22, 3.
Провести статистическую обработку данных.
13.2. Среднемесячная зарплата 100 работников хозяйства за истекший год, тыс. руб.:
3, 2; 3, 1; 2, 3; 3, 4; 3, 0; 3, 6; 2, 8; 3, 5; 2, 1; 1, 9; 2, 2; 3, 1; 3, 4; 2, 6; 2, 9; 3, 6; 2, 6; 3, 3; 3, 5; 3, 0; 2, 7; 1, 8; 2, 0; 2, 2; 2, 6; 2, 5; 4, 2; 2, 9; 1, 8; 2, 4; 3, 9; 1, 8; 1, 9; 3, 4; 4, 0; 3, 7; 2, 9; 2, 4; 2, 5; 2, 8; 4, 0; 2, 0; 3, 4; 1, 7; 3, 3; 3, 1; 2, 5; 2, 9; 2, 7; 2, 6; 2, 6; 3, 1; 3, 2; 3, 8; 2, 9; 4, 3; 3, 9; 2, 8; 2, 8; 2, 1; 2, 6; 4, 1; 2, 9; 2, 8; 2, 7; 3, 0; 3, 1; 2, 4; 2, 8; 3, 3; 1, 7; 3, 3; 3, 4; 3, 9; 3, 1; 3, 4; 3, 3; 3, 1; 3, 3; 3, 2; 2, 7; 2, 3; 2, 9; 3, 2; 3, 1; 2, 3; 3, 0; 3, 4; 3, 6; 2, 8; 3, 4; 2, 6; 2, 9; 2, 6; 3, 3; 3, 7; 3, 5; 3, 0; 1, 7; 1, 8.
Обработать данные 1- 60 работников хозяйства.
13.3. Обработать данные 11─ 70 работников хозяйства, представленные в 3.2.
13.4. Обработать данные 21─ 80 работников хозяйства, представленные в 3.2.
13.5.Обработать данные 31─ 90 работников хозяйства, представленные в 3.2.
13.6. Обработать данные 41─ 100 работников хозяйства, представленные в задаче 3.2.
13.7. Результаты взвешивания 90 коров, ц:
4, 5; 4, 7; 3, 4; 5, 4; 4, 6; 5, 0; 3, 8; 4, 7; 5, 6; 4, 0; 5, 1; 4, 9; 3, 3; 3, 5; 4, 3; 5, 5; 4, 5; 4, 24 5, 1; 4, 9; 4, 5; 3, 4; 4, 0; 5, 1; 4, 7; 5, 8; 4, 4; 4, 6; 4, 8; 5, 7; 3, 3; 4, 4; 4, 9; 3, 3; 5, 5; 4, 5; 5, 1; 3, 7; 4, 8; 5, 3; 4, 1; 4, 2; 5, 2; 4, 8; 3, 2; 3, 4; 5, 7; 4, 5; 4, 5; 4, 7; 4, 5; 4, 6; 3, 7; 5, 9; 4, 6; 4, 9; 4, 1; 4, 7; 5, 2; 4, 2; 5, 0; 4, 8; 3, 6; 3, 8; 4, 3; 5, 2; 4, 6; 4, 4; 5, 1; 5, 0; 4, 4; 3, 6; 4, 0; 5, 3; 4, 7; 5, 5; 4, 4; 4, 6; 4, 8; 5, 4; 3, 9; 4, 4; 4, 9; 3, 7; 5, 2; 4, 5; 5, 1; 4, 0; 4, 8; 5, 3.
Обработать данные взвешивания 1─ 60 коров.
13.8. Обработать данные взвешивания 11─ 70 коров, представленные в 3.7.
13.9. Обработать данные взвешивания 21 – 80 коров, представленные в 3.7.
13.10. Обработать данные взвешивания 31─ 90 коров, представленные в 3.7.
13.11. В случайном порядке отобрано 100 клубней картофеля и определена масса каждого клубня, г:
112, 210, 133, 215, 206, 80, 134, 145, 183, 251, 58, 142, 120, 177, 159, 111, 185, 200, 191, 96, 205, 138, 213, , 209, 77, 201, 131, 148, 180, 260, 60, 146, 117, 180, 156, 116, 181, 203, 188, 81, 120, 135, 220, 144, 152, 150, 110, 118, 140, 125, 208, 134, 214, 259, 195, , 85, 136, 53, 181, 256, 59, 59, 142, 122, 177, 160, 114, 183, 199, 197, 101, 202, 142, 218, 209, 79, 206, 137, 148, 180, 209, 65, 82, 88, 117, 180, 68, 117, 181, 202, 188, 94, 113, 135, 220, 144, 59, 69, 100, 91.
Обработать данные взвешивания 1─ 60 клубней картофеля.
13.12. Обработать данные взвешивания 11─ 70 клубней картофеля, представленные в 3.11.
13.13. Обработать данные взвешивания 21─ 80 клубней картофеля, представленные в 3.11.
13.14. Обработать данные взвешивания 31─ 90 клубней картофеля, представленные в 3.11.
13.15. Обработать данные взвешивания 41─ 100 клубней картофеля, представленные в задаче 3.11.
13.16. В 70 хозяйствах области затраты на животноводство (в десятках тыс. руб. на 100 голов):
25, 38, 53, 40, 43, 40, 38, 49, 27, 50, 20, 39, 61, 63, 44, 68, 59, 60, 58, 68, 39, 50, 42, 51, 47, 37, 62, 38, 35, 59, 23, 54, 60, 39, 61, 53, 49, 42, 41, 41, 33, 59, 31, 51, 38, 44, 67, 31, 40, 30, 52, 57, 39, 49, 41, 42, 43, 39, 17, 41, 19, 27, 46, 57, 66, 72, 70, 22, 32, 33.
Произвести обработку данных по 1─ 60 хозяйствам.
13.17. Обработать данные по 11─ 70 хозяйствам, представленные в задаче 3.16.
13.18.По 80 хозяйствам среднегодовой удой молока, ц, составил
23, 29, 39, 36, 32, 19, 33, 25, 30, 32, 29, 15, 14, 22, 28, 38, 31, 35, 23, 32, 42, 43, 22, 27, 30, 38, 35, 31, 29, 35, 32, 28, 40, 36, 29, 34, 31, 32, 36, 30, 32, 15, 35, 28, 28, 18, 27, 39, 30, 15, 14, 30, 42, 38, 35, 43, 39, 29, 18, 19, 24, 25, 23, 29, 39, 36, 19, 34, 24, 31, 33, 28, 16, 15, 23, 29, 38, 32, 34, 22.
Произвести обработку данных по 1─ 60 хозяйствам.
13.19. Произвести обработку данных по среднегодовому удою молока по 11─ 70 хозяйствам, представленным в 3.18.
13.20. Произвести обработку данных по среднегодовому удою молока по 21─ 80 хозяйствам, представленным в 3.18.
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Линейное программирование
Программные вопросы
1. Основная задача линейного программирования. Теорема об оптимальном плане.
2. Графический метод решения задач линейного программирования.
3. Симплекс-метод решения задач линейного программирования в канонической форме.
Решение типового примера
Пример 14.1. Требуется решить задачу линейного программирования графическим методом:
 
Решение. Построим сначала область допустимых решений, которая представляет собой множество решений системы линейных ограничений.
Графически решение каждого неравенства есть одна из полуплоскостей, на которые прямая линия ax +by =c делит координатную плоскость. Решением системы неравенств будет выпуклый многоугольник, представляющий собой пересечение полуплоскостей – решений каждого неравенства.
Пронумеруем каждое неравенство и решим его (см. рис.1.1)
1. 
Построим прямую  , для чего найдём координаты двух её точек, например, (0; 2) и (2; 4). Чтобы выбрать полуплоскость-решение для данного неравенства, подставим в это неравенство координаты любой точки, не лежащей на построенной прямой, например точки с координатами (0; 0). Получаем 0 – 0 +2 , для чего найдём координаты двух её точек, например, (0; 2) и (2; 4). Чтобы выбрать полуплоскость-решение для данного неравенства, подставим в это неравенство координаты любой точки, не лежащей на построенной прямой, например точки с координатами (0; 0). Получаем 0 – 0 +2  0. Это верное неравенство. Следовательно, полуплоскость, содержащая эту точку, будет являться решением неравенства 1. Стрелками отметим решение. 0. Это верное неравенство. Следовательно, полуплоскость, содержащая эту точку, будет являться решением неравенства 1. Стрелками отметим решение.
Аналогично строим решения каждого неравенства.
2. 
Строим прямую  , проходящую через точки с координатами (0; -3) и (2; 0). Решением неравенства является полуплоскость, содержащая начало координат (0, 0), так как: 3∙ 0 –2∙ 0 – 6 , проходящую через точки с координатами (0; -3) и (2; 0). Решением неравенства является полуплоскость, содержащая начало координат (0, 0), так как: 3∙ 0 –2∙ 0 – 6  0 - верное неравенство. 0 - верное неравенство.
3. 
Строим прямую 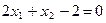 , проходящую через точки с координатами (0; 2) и (1; 0). Затем в неравенство подставляем координаты точки (0; 0): 2∙ 0 + 0 – 2 , проходящую через точки с координатами (0; 2) и (1; 0). Затем в неравенство подставляем координаты точки (0; 0): 2∙ 0 + 0 – 2  0. Так как это неравенство неверное, то решением является полуплоскость, не содержащая точку с координатами (0; 0). 0. Так как это неравенство неверное, то решением является полуплоскость, не содержащая точку с координатами (0; 0).
4. 
Прямая, определяемая уравнением  проходит через точку (0; 3) параллельно оси абсцисс. Полуплоскость, лежащая ниже этой прямой и есть решение данного неравенства. проходит через точку (0; 3) параллельно оси абсцисс. Полуплоскость, лежащая ниже этой прямой и есть решение данного неравенства.
Два последних неравенства  определяют первый квадрант координатной плоскости. определяют первый квадрант координатной плоскости.
На рис. 14.1 многоугольник ABCDE представляет собой область допустимых решений задачи линейного программирования.

Рис. 14. 1. Решение задачи линейного программирования.
Для нахождения оптимального решения построим вектор  (3; 2), координаты которого равны коэффициентам при переменных в целевой функции L. Этот вектор является нормальным вектором для линий уровня L=const, а также одну из линий уровня, например, (3; 2), координаты которого равны коэффициентам при переменных в целевой функции L. Этот вектор является нормальным вектором для линий уровня L=const, а также одну из линий уровня, например,  . Так, как задача на отыскание максимального значения целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой, то есть такой линии уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей. Эта прямая проходит через точку С пересечения прямых . Так, как задача на отыскание максимального значения целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой, то есть такой линии уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей. Эта прямая проходит через точку С пересечения прямых  и и  , для определения координат точки С решим систему уравнений , для определения координат точки С решим систему уравнений 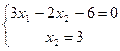 , получаем С(4; 3) в этой точке целевая функция достигает максимума , получаем С(4; 3) в этой точке целевая функция достигает максимума  . .
Ответ:  при Х*= (4; 3). при Х*= (4; 3).
Задачи контрольной работы
Решите задачи линейного программирования 14.1 – 14.20 графическим методом:
14.1.  14.2. 14.2. 
14.3.  14.4. 14.4. 
14.5.  14.6. 14.6. 
14.7. 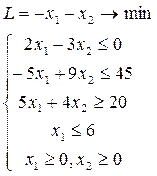 14.8. 14.8. 
14.9. 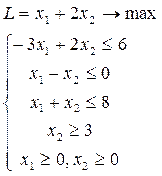 14.10. 14.10. 
14.11.  14.12. 14.12. 
14.13. 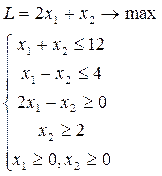 14.14. 14.14. 
14.15.  14.16. 14.16. 
14.17.  14.18. 14.18. 
14.19.  14.20. 14.20. 
Приложение 1
Значения функции 
| Целые и десятые доли х
| Сотые доли х
| |
|
|
|
|
|
|
|
|
|
| | 0, 0
| 0, 3989
| 0, 3989
| 0, 3989
| 0, 3988
| 0, 3986
| 0, 3984
| 0, 3982
| 0, 3980
| 0, 3977
| 0, 3973
| | 0, 1
|
|
|
|
|
|
|
|
|
|
| | 0, 2
|
|
|
|
|
|
|
|
|
|
| | 0, 3
|
|
|
|
|
|
|
|
|
|
| | 0, 4
|
|
|
|
|
|
|
|
|
|
| | 0, 5
|
|
|
|
|
|
|
|
|
|
|  0, 6 0, 6
|
|
|
|
|
|
|
|
|
|
| | 0, 7
|
|
|
|
|
|
|
|
|
|
| | 0, 8
|
|
|
|
|
|
|
|
|
|
| | 0, 9
|
|
|
|
|
|
|
|
|
|
| | 1, 0
| 0, 2420
| 0, 2396
| 0, 2371
| 0, 2347
| 0, 2323
| 0, 2299
| 0, 2275
| 0, 2251
| 0, 2227
| 0, 2203
| | 1, 1
|
|
|
|
|
|
|
|
|
|
| | 1, 2
|
|
|
|
|
|
|
|
|
|
| | 1, 3
|
|
|
|
|
|
|
|
|
|
| | 1, 4
|
|
|
|
|
|
|
|
|
|
| | 1, 5
|
|
|
|
|
|
|
|
|
|
| | 1, 6
|
|
|
|
|
|
|
|
|
|
| | 1, 7
|
|
|
|
|
|
|
|
|
|
| | 1, 8
|
|
|
|
|
|
|
|
|
|
| | 1, 9
|
|
|
|
|
|
|
|
|
|
| | 2, 0
| 0, 0540
| 0, 0529
| 0, 0519
| 0, 0508
| 0, 0498
| 0, 0488
| 0, 0478
| 0, 0468
| 0, 0459
| 0, 0449
| Окончание прил. 1
| Целые и десятые доли х
| Сотые доли х
| |
|
|
|
|
|
|
|
|
|
| | 2, 1
|
|
|
|
|
|
|
|
|
|
| | 2, 2
|
|
|
|
|
|
|
|
|
|
| | 2, 3
|
|
|
|
|
|
|
|
|
|
| | 2, 4
|
|
|
|
|
|
|
|
|
|
| | 2, 5
|
|
|
|
|
|
|
|
|
|
| | 2, 6
|
|
|
|
|
|
|
|
|
|
| | 2, 7
|
|
|
|
|
|
|
|
|
|
|  2, 8 2, 8
|
|
|
|
|
|
|
|
|
|
| | 2, 9
|
|
|
|
|
|
|
|
|
|
| | 3, 0
| 0, 0044
| 0, 0043
| 0, 0042
| 0, 0041
| 0, 0039
| 0, 0038
| 0, 0037
| 0, 0036
| 0, 0035
| 0, 0034
| | 3, 1
|
|
|
|
|
|
|
|
|
|
| | 3, 2
|
|
|
|
|
|
|
|
|
|
| | 3, 3
|
|
|
|
|
|
|
|
|
|
| | 3, 4
|
|
|
|
|
|
|
|
|
|
| | 3, 5
|
|
|
|
|
|
|
|
|
|
| | 3, 6
|
|
|
|
|
|
|
|
|
|
| | 3, 7
|
|
|
|
|
|
|
|
|
|
| | 3, 8
|
|
|
|
|
|
|
|
|
|
| | 3, 9
|
|
|
|
|
|
|
|
|
|
| | 4, 0
| 0, 0001
| 0, 0001
| 0, 0001
| 0, 0001
| 0, 0001
| 0, 0001
| 0, 0001
| 0, 0001
| 0, 0001
| 0, 0001
| | 4, 1
| 0, 0001338
|
|
|
|
|
|
|
|
|
| | 4, 5
| 0, 0000160
|
|
|
|
|
|
|
|
|
| | 5, 0
| 0, 0000015
|
|
|
|
|
|
|
|
|
|
Приложение 2
Значения функции 
| Целые и десятые доли х
| Сотые доли х
| |
|
|
|
|
|
|
|
|
|
| | 0, 0
| 0, 0000
| 0, 0040
| 0, 0080
| 0, 0120
| 0, 0160
| 0, 0199
| 0, 0239
| 0, 0279
| 0, 0319
| 0, 0359
| | 0, 1
| 0, 0398
| 0, 0438
| 0, 0478
| 0, 0517
| 0, 0577
| 0, 0596
| 0, 0636
| 0, 0675
| 0, 0714
| 0, 0753
| | 0, 2
| 0, 0793
| 0, 0832
| 0, 0871
| 0, 0910
| 0, 0948
| 0, 0987
| 0, 1026
| 0, 1064
| 0, 1103
| 0, 1141
| | 0, 3
| 0, 1179
| 0, 1217
| 0, 1255
| 0, 1293
| 0, 1331
| 0, 1368
| 0, 1406
| 0, 1443
| 0, 1480
| 0, 1517
| | 0, 4
| 0, 1554
| 0, 1591
| 0, 1628
| 0, 1664
| 0, 1700
| 0, 1736
| 0, 1772
| 0, 1808
| 0, 1844
| 0, 1879
|  0, 5 0, 5
| 0, 1915
| 0, 1950
| 0, 1985
| 0, 2019
| 0, 2054
| 0, 2088
| 0, 2123
| 0, 2157
| 0, 2190
| 0, 2224
| | 0, 6
| 0, 2257
| 0, 2291
| 0, 2324
| 0, 2357
| 0, 2389
| 0, 2422
| 0, 2454
| 0, 2486
| 0, 2517
| 0, 2549
| | 0, 7
| 0, 2580
| 0, 2611
| 0, 2642
| 0, 2673
| 0, 2703
| 0, 2734
| 0, 2764
| 0, 2794
| 0, 2823
| 0, 2852
| | 0, 8
| 0, 2881
| 0, 2910
| 0, 2939
| 0, 2967
| 0, 2995
| 0, 3023
| 0, 3051
| 0, 3078
| 0, 3106
| 0, 3133
| | 0, 9
| 0, 3159
| 0, 3186
| 0, 3212
| 0, 3238
| 0, 3264
| 0, 3289
| 0, 3315
| 0, 3340
| 0, 3365
| 0, 3389
| | 1, 0
| 0, 3413
| 0, 3438
| 0, 3461
| 0, 3485
| 0, 3508
| 0, 3531
| 0, 3554
| 0, 3577
| 0, 3599
| 0, 3621
| | 1, 1
| 0, 3643
| 0, 3665
| 0, 3686
| 0, 3708
| 0, 3729
| 0, 3749
| 0, 3770
| 0, 3790
| 0, 3810
| 0, 3830
| | 1, 2
| 0, 3849
| 0, 3869
| 0, 3883
| 0, 3907
| 0, 3925
| 0, 3944
| 0, 3962
| 0, 3980
| 0, 3997
| 0, 4015
| | 1, 3
| 0, 4032
| 0, 4049
| 0, 4066
| 0, 4082
| 0, 4099
| 0, 4115
| 0, 4131
| 0, 4147
| 0, 4162
| 0, 4177
| | 1, 4
| 0, 4192
| 0, 4207
| 0, 4222
| 0, 4236
| 0, 4251
| 0, 4265
| 0, 4279
| 0, 4292
| 0, 4306
| 0, 4319
| | 1, 5
| 0, 4332
| 0, 4345
| 0, 4357
| 0, 4370
| 0, 4382
| 0, 4394
| 0, 4406
| 0, 4418
| 0, 4429
| 0, 4441
| | 1, 6
| 0, 4452
| 0, 4463
| 0, 4474
| 0, 4484
| 0, 4495
| 0, 4505
| 0, 4515
| 0, 4525
| 0, 4535
| 0, 4545
| | 1, 7
| 0, 4554
| 0, 4564
| 0, 4573
| 0, 4582
| 0, 4591
| 0, 4599
| 0, 4608
| 0, 4616
| 0, 4625
| 0, 4633
| | 1, 8
| 0, 4641
| 0, 4649
| 0, 4656
| 0, 4664
| 0, 4671
| 0, 4678
| 0, 4686
| 0, 4693
| 0, 4699
| 0, 4706
| | 1, 9
| 0, 4713
| 0, 4719
| 0, 4726
| 0, 4732
| 0, 4738
| 0, 4744
| 0, 4750
| 0, 4756
| 0, 4761
| 0, 4767
| Окончание прил. 2
| Целые и десятые доли х
| Сотые доли х
| |
|
|
|
|
|
|
|
|
|
| | 2, 0
| 0, 4772
| 0, 4778
| 0, 4788
| 0, 4793
| 0, 4798
| 0, 4803
| 0, 4803
| 0, 4808
| 0, 4812
| 0, 4817
| | 2, 1
| 0, 4821
| 0, 4826
| 0, 4830
| 0, 4834
| 0, 4838
| 0, 4842
| 0, 4846
| 0, 4850
| 0, 4854
| 0, 4857
| | 2, 2
| 0, 4861
| 0, 4864
| 0, 4868
| 0, 4871
| 0, 4874
| 0, 4878
| 0, 4881
| 0, 4884
| 0, 4887
| 0, 4890
| | 2, 3
| 0, 4893
| 0, 4896
| 0, 4898
| 0, 4901
| 0, 4904
| 0, 4906
| 0, 4909
| 0, 4911
| 0, 4913
| 0, 4916
| | 2, 4
| 0, 4918
| 0, 4920
| 0, 4922
| 0, 4924
| 0, 4927
| 0, 4929
| 0, 4930
| 0, 4932
| 0, 4934
| 0, 4936
|  2, 5 2, 5
| 0, 4938
| 0, 4940
| 0, 4941
| 0, 4943
| 0, 4945
| 0, 4946
| 0, 4948
| 0, 4949
| 0, 4952
| 0, 4952
| | 2, 6
| 0, 4953
| 0, 4955
| 0, 4956
| 0, 4957
| 0, 4958
| 0, 4960
| 0, 4961
| 0, 4962
| 0, 4963
| 0, 4964
| | 2, 7
| 0, 4965
| 0, 4966
| 0, 4967
| 0, 4968
| 0, 4969
| 0, 4970
| 0, 4971
| 0, 4972
| 0, 4973
| 0, 4974
| | 2, 8
| 0, 4974
| 0, 4975
| 0, 4976
| 0, 4977
| 0, 4977
| 0, 4978
| 0, 4979
| 0, 4980
| 0, 4980
| 0, 4981
| | 2, 9
| 0, 4981
| 0, 4982
| 0, 4983
| 0, 4983
| 0, 4984
| 0, 4984
| 0, 4985
| 0, 4985
| 0, 4986
| 0, 4986
| | 3, 0
| 0, 4987
| 0, 4987
| 0, 4987
| 0, 4988
| 0, 4989
| 0, 4989
| 0, 4989
| 0, 4989
| 0, 4900
| 0, 4990
| | 3, 1
| 0, 4991
| 0, 4991
| 0, 991
| 0, 4991
| 0, 4991
| 0, 4992
| 0, 4992
| 0, 4992
| 0, 4993
| 0, 4993
| | 3, 2
| 0, 4993
| 0, 4993
| 0, 4994
| 0, 4994
| 0, 4994
| 0, 4994
| 0, 4995
| 0, 4995
| 0, 4995
| 0, 4995
| | 3, 3
| 0, 4995
| 0, 4996
| 0, 4996
| 0, 4996
| 0, 4996
| 0, 4996
| 0, 4996
| 0, 4996
| 0, 4997
| 0, 4997
| | 3, 4
| 0, 4997
| 0, 4997
| 0, 4997
| 0, 4997
| 0, 4997
| 0, 4997
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| | 3, 5
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 49986
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| | 3, 6
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4998
| 0, 4999
| 0, 4999
| 0, 4999
| | 3, 7
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| | 3, 8
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| | 3, 9
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| | 4, 0
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
| 0, 4999
|
Приложение 3
Значения функции Пуассона 
| l
m
| 0, 1
| 0, 2
| 0, 3
| 0, 4
| 0, 5
| 0, 6
| |
| 0, 904837
| 0, 818731
| 0, 740818
| 0, 670320
| 0, 606531
| 0, 548812
| |
| 0, 090484
| 0, 163746
| 0, 222245
| 0, 268128
| 0, 303265
| 0, 329287
| |
| 0, 004524
| 0, 016375
| 0, 033337
| 0, 053626
| 0, 075816
| 0, 098786
| |
| 0, 000151
| 0, 001091
| 0, 003334
| 0, 007150
| 0, 012636
| 0, 019757
| |
| 0, 000004
| 0, 000055
| 0, 000250
| 0, 000715
| 0, 001580
| 0, 002964
| |
| 0, 000000
| 0, 000002
| 0, 000015
| 0, 000057
| 0, 000158
| 0, 000356
| |
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000004
| 0, 000013
| 0, 000035
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000003
| |
|
|
|
|
|
|
| | l
m
| 0, 7
| 0, 8
| 0, 9
| 1, 0
| 2, 0
| 3, 0
| |
| 0, 496585
| 0, 449329
| 0, 406570
| 0, 367879
| 0, 135335
| 0, 049787
| |
| 0, 347610
| 0, 359463
| 0, 365913
| 0, 367879
| 0, 270671
| 0, 149361
| |
| 0, 121663
| 0, 143785
| 0, 164661
| 0, 183940
| 0, 270671
| 0, 224042
| |
| 0, 028388
| 0, 038343
| 0, 049398
| 0, 061313
| 0, 180447
| 0, 224042
| |
| 0, 004968
| 0, 007669
| 0, 011115
| 0, 015328
| 0, 090224
| 0, 168031
| |
| 0, 000695
| 0, 001227
| 0, 002001
| 0, 003066
| 0, 036089
| 0, 100819
| |
| 0, 000081
| 0, 000164
| 0, 000300
| 0, 000511
| 0, 012030
| 0, 050409
| |
| 0, 000008
| 0, 000019
| 0, 000039
| 0, 000073
| 0, 003437
| 0, 021604
| |
| 0, 000001
| 0, 000002
| 0, 000004
| 0, 000009
| 0, 000859
| 0, 008102
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000191
| 0, 002701
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000038
| 0, 000810
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000007
| 0, 000221
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000055
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000013
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000003
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
| Окончание прил. 3
 l
m l
m
| 4, 0
| 5, 0
| 6, 0
| 7, 0
| 8, 0
| 9, 0
| 10, 0
| |
| 0, 018316
| 0, 006738
| 0, 002479
| 0, 000912
| 0, 000335
| 0, 000123
| 0, 000045
| |
| 0, 073263
| 0, 033690
| 0, 014873
| 0, 006383
| 0, 002684
| 0, 001111
| 0, 000454
| |
| 0, 146525
| 0, 084224
| 0, 044618
| 0, 022341
| 0, 010735
| 0, 004998
| 0, 002270
| |
| 0, 195367
| 0, 140374
| 0, 089235
| 0, 052129
| 0, 028626
| 0, 014994
| 0, 007567
| |
| 0, 195367
| 0, 175467
| 0, 133853
| 0, 091226
| 0, 057252
| 0, 033737
| 0, 018917
| |
| 0, 156293
| 0, 175467
| 0, 160623
| 0, 127717
| 0, 091604
| 0, 060727
| 0, 037833
| |
| 0, 104194
| 0, 146223
| 0, 160623
| 0, 149003
| 0, 122138
| 0, 091090
| 0, 063055
| |
| 0, 059540
| 0, 104445
| 0, 137677
| 0, 149003
| 0, 139587
| 0, 117116
| 0, 090079
| |
| 0, 029770
| 0, 065278
| 0, 103258
| 0, 130377
| 0, 139587
| 0, 131756
| 0, 112600
| |
| 0, 013231
| 0, 036266
| 0, 068838
| 0, 101405
| 0, 124077
| 0, 131756
| 0, 125110
| |
| 0, 005292
| 0, 018133
| 0, 041303
| 0, 070983
| 0, 099662
| 0, 118580
| 0, 125110
| |
| 0, 001925
| 0, 008242
| 0, 022529
| 0, 045171
| 0, 072190
| 0, 097020
| 0, 113740
| |
| 0, 000642
| 0, 003434
| 0, 011262
| 0, 026350
| 0, 048127
| 0, 072765
| 0, 094780
| |
| 0, 000197
| 0, 001321
| 0, 005199
| 0, 014188
| 0, 029616
| 0, 050376
| 0, 072908
| |
| 0, 000056
| 0, 000472
| 0, 002228
| 0, 007094
| 0, 016924
| 0, 032384
| 0, 052077
| |
| 0, 000015
| 0, 000157
| 0, 000891
| 0, 003311
| 0, 009026
| 0, 019431
| 0, 034718
| |
| 0, 000004
| 0, 000049
| 0, 000334
| 0, 001448
| 0, 004513
| 0, 010930
| 0, 021699
| |
| 0, 000001
| 0, 000014
| 0, 000118
| 0, 000596
| 0, 002124
| 0, 005786
| 0, 012764
| |
| 0, 000000
| 0, 000004
| 0, 000039
| 0, 000232
| 0, 000944
| 0, 002893
| 0, 007091
| |
| 0, 000000
| 0, 000001
| 0, 000012
| 0, 000085
| 0, 000397
| 0, 001370
| 0, 003732
| |
| 0, 000000
| 0, 000000
| 0, 000004
| 0, 000030
| 0, 000159
| 0, 000617
| 0, 001866
| |
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000010
| 0, 000061
| 0, 000264
| 0, 000889
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000003
| 0, 000022
| 0, 000108
| 0, 000404
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000008
| 0, 000042
| 0, 000176
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000003
| 0, 000016
| 0, 000073
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000006
| 0, 000029
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000002
| 0, 000011
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
| 0, 000004
| |
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000000
| 0, 000001
|
Приложение 4
Критические точки распределения c2
| Число степеней свободы k
| Уровень значимости a
| | 0, 01
| 0, 025
| 0, 05
| 0, 95
| 0, 975
| 0, 89
| |
| 6, 6
| 5, 0
| 3, 8
| 0, 0039
| 0, 00098
| 0, 00016
| |
| 9, 2
| 7, 4
| 6, 0
| 0, 103
| 0, 051
| 0, 020
| |
| 11, 3
| 9, 4
| 7, 8
| 0, 352
| 0, 216
| 0, 115
| |
| 13, 3
| 11, 1
| 9, 5
| 0, 711
| 0, 484
| 0, 297
| |
| 15, 1
| 12, 8
| 11, 1
| 1, 15
| 0, 831
| 0, 554
| |
| 16, 8
| 14, 4
| 12, 6
| 1, 64
| 1, 24
| 0, 872
| |
| 18, 5
| 16, 0
| 14, 1
| 2, 17
| 1, 69
| 1, 24
| |
| 20, 1
| 17, 5
| 15, 5
| 2, 73
| 2, 18
| 1, 65
| |
| 21, 7
| 19, 0
| 16, 9
| 3, 33
| 2, 70
| 2, 09
| |
| 23, 2
| 20, 5
| 18, 3
| 3, 94
| 3, 25
| 2, 56
| |
| 24, 7
| 21, 9
| 19, 7
| 4, 57
| 3, 82
| 3, 05
| |
| 26, 2
| 23, 3
| 21, 0
| 5, 23
| 4, 40
| 3, 57
| |
| 27, 7
| 24, 7
| 22, 4
| 5, 89
| 5, 01
| 4, 11
| |
| 29, 1
| 26, 1
| 23, 7
| 6, 57
| 5, 63
| 4, 66
| |
| 30, 6
| 27, 5
| 25, 0
| 7, 26
| 6, 26
| 5, 23
| |
| 32, 0
| 28, 8
| 26, 3
| 7, 96
| 6, 91
| 5, 81
| |
| 33, 4
| 30, 2
| 27, 6
| 8, 67
| 7, 56
| 6, 41
| |
| 34, 8
| 31, 5
| 28, 9
| 9, 39
| 8, 23
| 7, 01
| |
| 36, 2
| 32, 9
| 30, 1
| 10, 1
| 8, 91
| 7, 63
| |
| 37, 6
| 34, 2
| 31, 4
| 10, 9
| 9, 59
| 8, 26
| |
| 38, 9
| 35, 5
| 32, 7
| 11, 6
| 10, 3
| 8, 90
| |
| 40, 3
| 36, 8
| 33, 9
| 12, 3
| 11, 0
| 9, 54
| |
| 41, 6
| 38, 1
| 35, 2
| 13, 1
| 11, 7
| 10, 2
| |
| 43, 0
| 39, 4
| 36, 4
| 13, 8
| 12, 4
| 10, 9
| |
| 44, 3
| 40, 6
| 37, 7
| 14, 6
| 13, 1
| 11, 5
| |
| 45, 6
| 41, 9
| 38, 9
| 15, 4
| 13, 8
| 12, 2
| |
| 47, 0
| 43, 2
| 40, 1
| 16, 2
| 14, 6
| 12, 9
| |
| 48, 3
| 44, 5
| 41, 3
| 16, 9
| 15, 3
| 13, 6
| |
| 49, 6
| 45, 7
| 42, 6
| 17, 7
| 16, 0
| 14, 3
| |
| 50, 9
| 47, 0
| 43, 8
| 18, 5
| 16, 8
| 15, 0
|
Приложение 5
Значения tp(p, n)
| n
| P
| n
| P
| | 0, 95
| 0, 99
| 0, 999
| 0, 95
| 0, 99
| 0, 999
| |
| 2, 78
2, 57
2, 45
2, 37
2, 31
2, 26
2, 23
2, 20
2, 18
2, 16
2, 15
2, 13
2, 12
2, 11
2, 10
| 4, 60
4, 03
3, 71
3, 50
3, 36
3, 25
3, 17
3, 11
3, 06
3, 01
2, 98
2, 95
2, 92
2, 90
2, 88
| 8, 61
6, 86
5, 96
5, 41
5, 04
4, 78
4, 59
4, 44
4, 32
4, 22
4, 14
4, 07
4, 02
3, 97
3, 92
|
¥
| 2, 093
2, 064
2, 045
2, 032
2, 023
2, 016
2, 009
2, 001
1, 996
1, 991
1, 987
1, 984
1, 980
1, 960
| 2, 861
2, 797
2, 756
2, 720
2, 708
2, 692
2, 679
2, 662
2, 649
2, 640
2, 633
2, 627
2, 617
2, 576
| 3, 883
3, 745
3, 652
3, 600
3, 558
3, 527
3, 502
3, 464
3, 439
3, 418
3, 403
3, 392
3, 374
3, 291
|
Приложение 6
Значения q = q(p, n)
| n
| P
| n
| P
| | 0, 95
| 0, 99
| 0, 999
| 0, 95
| 0, 99
| 0, 999
| |
| 1, 37
1, 09
0, 92
0, 80
0, 71
0, 65
0, 59
0, 55
0, 52
0, 48
0, 46
0, 44
0, 42
0, 40
0, 39
| 2, 67
2, 01
1, 62
1, 38
1, 20
1, 08
0, 98
0, 90
0, 83
0, 78
0, 73
0, 70
0, 66
0, 63
0, 60
| 5, 64
3, 88
2, 98
2, 42
2, 06
1, 80
1, 60
1, 45
1, 33
1, 23
1, 15
1, 07
1, 01
0, 96
0, 92
|
| 0, 37
0, 32
0, 28
0, 26
0, 24
0, 22
0, 21
0, 188
0, 174
0, 161
0, 151
0, 143
0, 115
0, 099
0, 089
| 0, 58
0, 49
0, 43
0, 38
0, 35
0, 32
0, 30
0, 269
0, 245
0, 226
0, 211
0, 198
0, 160
0, 136
0, 120
| 0, 88
0, 73
0, 63
0, 56
0, 50
0, 46
0, 43
0, 38
0, 34
0, 31
0, 29
0, 27
0, 211
0, 185
0, 162
|
Популярное:
|

