
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Кинематика поступательного и вращательного движенияСтр 1 из 16Следующая ⇒
Тестовые задания
1.1. Вектор скорости … 1) является количественной мерой изменения положения материальной точки 2) всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело 3) всегда направлен вдоль вектора перемещения 4) всегда направлен вдоль вектора ускорения 5) направлен перпендикулярно радиус-вектору материальной точки
1.2. Вектор средней скорости материальной точки совпадает по направлению с … 1) касательной к траектории 2) радиус-вектором, определяющим положение точки 3) вектором полного ускорения 4) вектором нормального ускорения 5) вектором перемещения
1.3. Материальная точка движется равномерно по окружности радиусом R с периодом Т. Модуль вектора средней скорости за четверть оборота равен … 1) 1.4. Материальная точка движется равномерно по окружности со скоростью 1) 0 2)
1.5. Материальная точка движется равномерно по окружности радиусом 1)
1) 6 2) 5, 5 3) 7 4) 5 5) 8
1.7. Зависимость скорости движения материальной точки по прямой от времени дана на рисунке. Среднее значение модуля скорости движения материальной точки в интервале времени 0-5 с равно … м/с. 1) 1, 5 2) 0, 25 3) 2, 5 4) 0, 2 5) 1, 4
1.8. Поезд движется на подъеме со скоростью 1)
1.9. Радиус-вектор частицы определяется выражением 1) 15 2) 20 3) 21 4) 35 5) 42
1.10. Материальная точка движется так, что радиус-вектор меняется со временем по закону 1) 2) 3) 4) 5)
1.11. Радиус-вектор точки изменяется со временем по закону 1) 12, 2 2) 24, 1 3) 24, 3 4) 26 5) 29
1.12. Радиус-вектор частицы изменяется со временем по закону
1) 1 2) 2 3) 3 4) 4 5) 5
1.13. Из точек А и В навстречу друг другу движутся два тела. Уравнения движения тел имеют вид: 1) 5 2) 11, 2 3) 10 4) 7, 8 5) 5, 6
1.14. Две материальные точки движутся согласно уравнениям: 1) 0, 94 2) 0, 54 3) 0, 65 4) 0, 74 5) 0, 82
1.15. Зависимость пройденного телом пути от времени дается уравнением 1) 11 2) 5 3) 5, 5 4) 6 5) 7 1.16. Две материальные точки движутся согласно уравнениям: 1) 1, 00 2) 0, 235 3) 0, 542 4) 0, 845 5) 0, 9
1.17. Тело начинает двигаться из состояния покоя с постоянным ускорением 2 см/с2. За третью секунду своего движения оно пройдет путь … см. 1) 9 2) 2 3) 3 4) 4 5) 5 1.18. Материальная точка начинает двигаться вдоль прямой так, что её ускорение прямо пропорционально квадрату времени ( 1) от времени не зависит 2)
1.19. Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 100 м из него выбрасывается вверх предмет со скоростью 2 м/с относительно вертолета. Предмет упадет на землю через … с. 1) 4, 5 2) 5, 3 3) 5, 6 4) 5, 8 5) 6, 0
1.20. Из одной и той же точки с интервалом 2 с брошены вертикально вверх два шарика с одинаковыми скоростями 30 м/с. Они столкнутся после броска первого шарика через … с. 1) 1 2) 2 3) 3 4) 4 5) 5 1.21. Камень падает с высоты 1) 1050 2) 150 3) 300 4) 450 5) 600
1.22. Мяч брошен под углом 60º к горизонту с начальной скоростью 10 м/с. Скорость мяча через 0, 2 с после броска равна … м/с. 1) 2 2) 8, 4 3) 8, 7 4) 9, 2 5) 12, 5 1.23. Камень брошен с башни в горизонтальном направлении. Через 3 с вектор скорости камня составил угол в 45º с горизонтом. Начальная скорость камня равна … в м/с. 1) 10 2) 15 3) 3 4) 20 5) 30
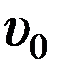 . Его траектория в однородном поле тяжести изображена на рисунке. Модули нормального аn и тангенциального аτ ускорений на участке А-В-С соответственно … . Его траектория в однородном поле тяжести изображена на рисунке. Модули нормального аn и тангенциального аτ ускорений на участке А-В-С соответственно …
1) увеличиваются; увеличиваются 2) уменьшаются; уменьшаются 3) увеличиваются; уменьшаются 4) уменьшаются; увеличиваются 5) уменьшаются; не изменяются 1.25. Тело брошено под углом 1) 1.26. Тело брошено под углом 1) 0 2)
1.27. Скорость камня в точке его падения составила с горизонтом угол 1)
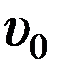 и и 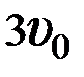 . Если сопротивлением воздуха пренебречь, то соотношение дальностей полета S2 / S1 равно … . Если сопротивлением воздуха пренебречь, то соотношение дальностей полета S2 / S1 равно …
1)
1) а 2) б 3) в 4) г
1.30. Материальная точка движется замедленно по криволинейной траектории. Направление скорости показано на рисунке. Направление векторов полного и тангенциального ускорений правильно изображено на рисунках соответственно …
1) в; г 2) а; б 3) б; а 4) а; в 5) г; а 1.31. Материальная точка М движется по окружности со скоростью
1) 5 2) 1 3) 2 4) 3 5) 4 1.32. При равнозамедленном движении материальной
1) 1 2) 2 3) 3 4) 4 5) равен нулю
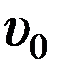 . Его траектория в поле силы тяжести изображена на рисунке. Модуль полного ускорения камня … . Его траектория в поле силы тяжести изображена на рисунке. Модуль полного ускорения камня …
1) максимален в т. А и Е 2) максимален в т. В и D 3) во всех точках одинаков 4) максимален в т. С
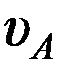 и величины скорости тела в т. В и величины скорости тела в т. В 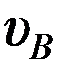 справедливо соотношение … справедливо соотношение …
1) 3) 5) h fKzkYxUlo6AdYPeGkbCeeUdQWOfjm77Lsw6yCZruEZd6QrAr7NrwMzFtx5meNBg5GSUZSafe3lYa vQVlPVXvqpmqoMiFjIx+yBgPQ60HkpL4sNY0yRmWzoKypkr7EAnKJVPZI6akk8rYtH6MIOPmZ+UX z7XkellZUJ4oVi8w87rE9RYCMu2y9KCJl7Vhek6nKfgciuWUgLo8gF/y0lpQ/rPqXTUEWSoCRCBF RM71GL8A6dcmmGLTf5vvr+l7bArWynwuyxO+jglNmbQWlCmxPqWXHCEgozvyMj0jtSJOi5WneEab tADNCNQ0irUdydpG+nWJEC9CATeTTkkSmWsqIGs2yysyBJ0EDciAo7xEFmxSIbnpJShQdklLNFOt gUqZ9BYUmN7jIlSK2yK5yCJoQILizorkJKugIrlRUCkaBZWCmc3+AdOizh2wLk2pAAAAAElFTkSu QmCCUEsBAi0AFAAGAAgAAAAhALGCZ7YKAQAAEwIAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50 X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAA7AQAA X3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA/Y4FPRcCAABjBAAADgAAAAAAAAAAAAAAAAA6AgAA ZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAqiYOvrwAAAAhAQAAGQAAAAAAAAAAAAAAAAB9 BAAAZHJzL19yZWxzL2Uyb0RvYy54bWwucmVsc1BLAQItABQABgAIAAAAIQDitnMz4AAAAAkBAAAP AAAAAAAAAAAAAAAAAHAFAABkcnMvZG93bnJldi54bWxQSwECLQAKAAAAAAAAACEAr1K8f8wFAADM BQAAFAAAAAAAAAAAAAAAAAB9BgAAZHJzL21lZGlhL2ltYWdlMS5wbmdQSwUGAAAAAAYABgB8AQAA ewwAAAAA "> 1) не изменяется 2) увеличивается 3) уменьшается
1) уменьшается 2) не изменяется 3) увеличивается
1.37. Материальная точка движется равномерно по окружности радиусом 1) 1.38. Точка движется по окружности радиусом R = 2 м согласно уравнению l = Аt 3, А = 2 м/с3, l – длина дуги от начала движения. Нормальное ускорение равно тангенциальному в момент времени … с. 1) 2 2) 0, 874 3) 0, 760 4) 0, 667 5) 0, 3 1.39. Две материальные точки начинают двигаться по окружности из одной начальной точки: первая с ускорением 0, 10 рад/с2, вторая – с ускорением 0, 15 рад/с2. Впервые после начала движения они встретятся через … с. 1) 0, 2 2) 31, 7 3) 47, 5 4) 15, 8 5) 75, 0 1.40. Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением 1) 1 2) 2 3) 2, 5 4) 3 5) 4
1) 5 2) 4 3) 1 4) 3 5) 2 1.42. Материальная точка движется равнозамедленно по окружности, лежащей в вертикальной плоскости, по часовой стрелке. Вектора угловой скорости и углового ускорения направлены соответственно … 1) к нам; от нас 2) по касательной к траектории; к нам 3) к нам; по радиусу от центра 4) от нас; по касательной к траектории 5) от нас; к нам
1.43. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости ω Z(t) так, как показано на рисунке. Вектор углового ускорения
1) от 0 до t1 и от t3 до t4 2) от t1 до t2 и от t3 до t4 3) от 0 до t1 и от t1 до t2 4) от t2 до t3и от t3 до t4 5) от t1 до t2 и от t2 до t3 1.44. Закон изменения угла поворота φ со временем имеет вид 1) 19; 56 2) 56; 46 3) 88; 56 4) 86; 19 5) 76; 29 1.45. Точка вращается по окружности радиусом А) Б) В) Г) Д) 1) А; Г 2) В; А 3) Д; Г 4) Д; Б 5) А; Б
1.46. Тело вращается вокруг неподвижной оси по закону 1) 3, 20 2) 1, 65 3) 1, 60 4) 0, 40 5) 0
1.47. На вал радиусом 10 см намотана нить, к концу которой привязана гиря. Опускаясь равноускоренно, гиря прошла расстояние 5 см за 2 с. Тангенциальное ускорение точки, лежащей на поверхности вала, равно … см/с2. 1) 25 2) 0, 5 3) 5 4) 2, 5 5) 3, 5
1.48. Частица из состояния покоя начала двигаться по дуге окружности радиусом R = 1 м с постоянным угловым ускорением ε = 2 рад/с2. Отношение нормального ускорения к тангенциальному через одну секунду равно … 1) 8 2) 2 3) 1 4) 4 5) 3
1.49. Материальная точка вращается в горизонтальной плоскости относительно неподвижной оси с угловым ускорением ε = А t2, где А = 2 рад/с4. При t = 0 ω 0 = 0. Закон изменения угловой скорости имеет вид … 1) ω = 3/2 t 3 2) ω = 2t 3 3) ω = 2/3 t 3 4) ω = 4t 5) ω = 4t 3 1.50. Закон изменения угловой скорости материальной точки имеет вид 1) 6 2) 40 3) 65 4) 80 5) 125
1.51. Маховик вращается равнозамедленно с угловым ускорением ε = 2 рад/с2. Угол поворота φ при изменении частоты вращения от n1 = 240 мин –1 до n2 = 90 мин –1 равен … рад. 1) 4 2) 1479 3) 136 4) 22 5) 5
1.52. Тело движется по окружности так, что его угловая скорость изменяется по закону 1) 4 2) 5 3) 6, 28 4) 10 5) 12, 5 1.53. Если А) Г) 1) В; Д; А 2) Д; В; Б 3) В; Г; А 4) Д; Б; А 5) Г; В; Б
Задачи
1.54. По гладкой наклонной доске пустили катиться снизу вверх маленький брусок. На расстоянии l = 30 см брусок побывал дважды: через t1 = 1 с и через t2 = 2 c после начала движения. Определите начальную скорость бруска
1.55. Движение точки по кривой задано уравнениями 1.56. С башни брошен камень в горизонтальном направлении с начальной скоростью 40 м/с. Вычислить скорость камня через 3 с после начала движения. Какой угол образует вектор скорости камня с плоскостью горизонта в этот момент?
1.57. Снаряд вылетел со скоростью 30 м/с под углом 60º к горизонту. Чему равен радиус кривизны траектории снаряда через 2 с после выстрела?
1.58. Мяч брошен со скоростью
1.59. Под каким углом к горизонту надо бросить тело, чтобы центр кривизны его траектории в вершине находился на земле?
1.60. Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением S = At3, где А = 0, 1 см/с3. Найдите нормальное (аn) и тангенциальное (аτ ) ускорения точки в момент, когда линейная скорость точки
1.61. Точка движется по окружности радиусом
1.62. Зависимость угла поворота от времени для точки, лежащей на ободе колеса радиусом R, задается уравнением 1.63. Диск радиусом 10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 0, 5 рад/с2. Найдите касательное, нормальное и полное ускорения точек на окружности диска в конце второй секунды после начала вращения.
1.64. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R = 10 м. Уравнение движения автомобиля
1.65. Диск радиусом R =10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением
1.66. Материальная точка начинает движение по окружности радиусом 12, 5 см с постоянным тангенциальным ускорением 0, 5 см/с2. Определите момент времени, когда угол между векторами ускорения и скорости равен 45º и путь, пройденный точкой до этого момента.
1.67. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аτ . Найдите тангенциальное ускорение аτ точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки
Популярное:
|
Последнее изменение этой страницы: 2016-06-04; Просмотров: 1504; Нарушение авторского права страницы