Неоклассическая факторная модель роста.
Первоначально использовалась модель Кобба-Дугласа, представляющая со-
бой производственную функцию'

где Y - объем производства, L - затраты труда, К - затраты капитала, α и β сте-
пенные коэффициенты.
Из производственной функции ясно, что для обеспечения экономического
роста необходимо увеличивать либо капитал, либо трудовые ресурсы, либо оба
фактора одновременно. Здесь труд и капитал являются взаимозаменяемыми и
сумма коэффициентов эластичности выпуска по факторам равна единице (даль-
нейшие расчеты дали значения: (α = 3/4, (β = 1/4). Так как возможности трудового
фактора ограничены, то главным источником роста становится капитал, увели-
чить который можно, наращивая инвестиции. Однако функция не учитывает из-
менения качества производственных факторов, т.е влияния технического прогрес-
са, а значит, приемлема лишь для экстенсивного экономического роста
(рис. 14.2 и 14.3).
| Рис. 14.3. Влияние прироста массы капитала на производственную функцию
|
Рис. 14.2. Производственная функция
с переменным объемом затрат
труда
Модель Солоу. Модель, представленная Р. Солоу в 1956 г., была предназна-
чена главным образом для устранения нестабильности динамического равновесия
в неокейнсианских моделях.
Вместо производственной функции с невзаимозаменяемостью факторов
(леонтьевского типа) Солоу включил в свою модель производственную функцию
Кобба-Дугласа, в которой труд и капитал являются взаимозаменяемыми (субсти-
тутами), а конкуренция - совершенная: Y = F(K, L). При этом все переменные вы-
ражаются в виде показателей на душу населения (предполагаем, что население и
рабочая сила идентичны).
Параметром, обеспечивающим равновесный рост в модели Солоу, является
капиталовооруженность труда, т.е. количество капитала на единицу труда, K/L,
или k. Средняя производительность труда есть функция от его капиталовоору-
женности. Обозначив выпуск на одного работающего, Y/L, через q, запишем про-
изводственную функцию в следующем виде:

Рис. 14.4. Производственная функция в модели Солоу
Учтем, что инвестиции (I) равны сбережениям (S) в данной стране: I = S.
Изменения основного капитала (К) равны чистым инвестициям, т.е. инвестициям
за вычетом амортизации (dK). В этом случае изменение общего объема производ-
ственных фондов равно инвестициям минус амортизация:
∆ K = I-dK, (14.12)
или сбережения минус амортизация:
∆ K=SY-dK, (14.13)
а в расчете на одну рабочую силу:

Предположим, что население (рабочая сила) растет с постоянным темпом п
(n = ∆ L/L), введем его в уравнение (14.14) и осуществим некоторые преобразова-
ния, так что в итоге получим основное уравнение накопления капитала:

По мере роста капиталовооруженности труда его производительность уве-
личивается, но в убывающем темпе, так как снижается предельная производи-
тельность капитала (рис. 14.4).

Оно показывает, что рост капитала на одного работающего (∆ К) равен сбе-
режениям на душу населения Sq минус (n + d)K. Иначе говоря: сбережения,
идущие на рост фондовооруженности, равны среднедушевым сбережениям
минус сбережения, идущие на расширение капитала.
Для достижения устойчивого состояния необходимо, чтобы выполнялось
точное равенство среднедушевых сбережений и сбережений, идущих на расшире-
ние капитала (увеличение числа работающих), чтобы ∆ К = 0. Формально это
можно записать в виде:
Sq = (n + d)K. (14.16)
Устойчивое состояние сопровождается ростом выпуска с положительным
темпом п. Объем производственных фондов также возрастает с темпом п. По-
скольку как L, так и К растут с темпом п, то выпуск также растет с темпом п.
Устойчивое состояние в экономике характеризует рис. 14.5.
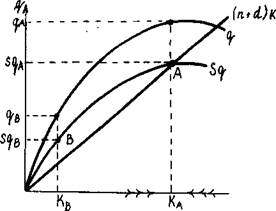
Рис. 14.5. Устойчивое состояние равновесия в экономике
Производственную функцию изображает кривая q (как на рис. 14.4), кривая
Sq показывает объем сбережений на душу населения. Поскольку сбережения
являются постоянной долей S выпуска (0< S< 1), эта новая кривая имеет тот же
вид, что и производственная функция. Поскольку S< 1, то новая кривая лежит ни-
же производственной функции. Линия (n + d)K - это прямая, проходящая через
начало координат под углом (n + d).
~~~ В устойчивом состоянии прямая (n + d)K и кривая Sq должны пересекаться,
так как Sq = (n + d)KA. В том случае, когда отношение " капитал - труд" (фондово-
оруженность) равно КA, а выпуск на душу населения (средняя производитель-
ность) равен qA, сберегается ровно столько, сколько нужно для того, чтобы про-
исходило расширение капитала, т.е. SqA = (n+d)KA. В этом случае размер средне-
душевых сбережений достаточен для того, чтобы оснастить новые рабочие места
и заменить выбывший капитал, не вызвав изменений в фондовооруженности.
Слева от точки А кривая Sq расположена выше, чем кривая (n + d)K. Это
означает, что сбережений больше, чем требуется для расширения капитала. Сле-
довательно, слева от точки А фондовооруженность растет, т.е. растут производст-
венные фонды на одного работающего (∆ К> 0), и будет иметь тенденция к росту
К, что показано стрелками на оси X. Справа от точки А имеем Sq< (n + d)K, а зна-
чит, К < 0. Поэтому справа от точки А будет иметь тенденция к понижению К, что
показано стрелками на горизонтальной оси.
Если страна находится на низком уровне развития, когда отношение
" капитал - труд" равно KB, средняя производительность также весьма низкая: qB.
Из-за малого количества производственных фондов необходимость направлять
сбережения на расширение капитала невелика, т.е. (n + d)KB мало. Поэтому объем
среднедушевых сбережений, который равен Squ, превышает потребности расши-
рения капитала и фондовооруженность растет. Растет и выпуск q; экономика дви-
жется вдоль графика производственной функции вправо от В, пока не достигнет
равновесия в точке А.
В конечном счете модель Солоу гарантирует не только возможность равно-
весного экономического роста, т.е. развития при полной занятости и полном ис-
пользовании капитала, но также и устойчивость этого роста в том смысле, что при
отклонении системы от линии равновесного развития вступают в действие внут-
ренние механизмы, способные гарантировать возвращение к состоянию
равновесия. Динамичные системы, в которых переменные обладают свойством автоматически возвращаться к состоянию устойчивого равновесия, наз-ся стабильными системами. Следовательно модель роста Солоу описывает стабильный динамический процесс роста.
Возникает вопрос: какие размеры накопления капитала являются оптималь-
ными? Накопление капитала, обеспечивающее устойчивое состояние с наивыс-
шим уровнем потребления, называется золотым правилом накопления. Иначе
говоря, должна быть определена оптимальная норма сбережения. Она равна эла-
стичности объема производства по капиталу: вся прибыль (л) должна быть инве-
стирована: π /Y = I/Y.
Модель Солоу может быть расширена путем введения различных показате-
лей. В последнее время особое значение придается техническому прогрессу. Он
включается в модели двумя способами: в качестве самостоятельного фактора на-
ряду с трудом и капиталом и в виде условного увеличения используемого количе-
ства труда и капитала. В данном случае необходимо учесть разновидности техни-
ческого прогресса. Все зависит от эластичности замещения труда и капитала. Не
нейтральный НТП описывается производственными функциями с переменной
эластичностью замещения Если замещается (экономится) труд за счет роста за-
трат капитала, то НТП называется трудосберегающим. Если замещается (эконо-
мится) капитал за счет роста затрат труда, то НТП называется капиталосберегаю-
щим. Если соотношение факторов производства остается неизменным, то эла-
стичность замещения постоянна. Такой НТП называется нейтральным и описыва-
ется производственной функцией с постоянной эластичностью замещения.
Указанный принцип, называемый также критерием Дж Хикса, дает самое
общее представление о нейтральности НТП и может быть дополнен другими кри-
териями: нейтральность по Харроду и Солоу. Лишь такой вид технического про-
гресса обеспечивает возможность равновесного роста, при котором производи-
тельность и капиталовооруженность труда растут с одинаковым темпом, а капи-
талоемкость не меняется.
Исследования экономического роста привели к созданию универсальной
модели Леонтьева " затраты-выпуск", в которой он представил основные матери-
альные и стоимостные потоки национального хозяйства. Схему баланса этих по-
токов можно показать в виде шахматной таблицы и системы уравнений.
Популярное:

