Система MathCad,основные функции
Определение: Уравнение вида ax+b=0 с заданным базовым множеством Gx, a из Ga , b из Gb называется линейным уравнением.
Этапы решения при помощи Mathcad:
1. Ввести уравнение (знак " =" вводится при помощи комбинации [Ctrl++]).
2. Выделить курсором переменную, относительно которой должно быть решено уравнение.
3. Выбрать команду Solve (Вычислить) подменю Variable (Переменные) меню Symbolics (Символы).
При решении линейных уравнений (без параметров) или дробных уравнений, которые сводятся к линейным, MathCAD находит все существующие решения. Однако при этом следует правильно интерпретировать сообщения, выдаваемые системой.
Нормальный случай.
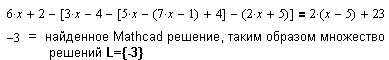
| В качестве решения MathCAD выдает число - это означает,
|
что уравнение однозначно разрешимо (однозначное решение линейного уравнения над множеством действительных чисел, которое одновременно является областью определения этого уравнения).
Решение отсутствует.
Рассмотрим другой пример: 
| После выполнения описанных выше действий для нахождения решения Mathcad выдает сообщение о том, что решение не найдено.
|
Проанализировав данное уравнение приходим к выводу, что выданное Mathcad сообщение означает, что решений нет L={}.
MathCAD выдает сообщение " Решение не найдено", даже если уравнение имеет " формальное решение", которое не принадлежит области определения (смотри примеры ниже).
Многозначность.
Если в качестве решения MathCAD выдает имя переменной, это означает, что
множество решений уравнения совпадает с областью определения. Однако, такие понятия, как множество решений уравнения и область определения, отсутствуют в MAthCAD и он не выписывает оболасть определения. Вы можете найти область определения, решая с помощью Mathcad систему неравенств или уравнений
 
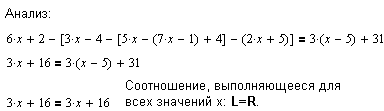
| Такой результат, выданный Mathcad после выполнения действий по решению уравнения, означает, что любое значение x из базового множества удовлетворяет этому уравнению, т. е. L=R.
|
Дробные уравнения
| Команда Solve (Вычислить) из подменю Variable (Переменные) меню Symbolics (Символы)выдает множество решений: L = {6}.
|
| Решение 6 копируем в буфер, а затем выделяем маркером переменную x и активизируем команду Substitute (Замена) подменю Variable (Переменные) меню Symbolics (Символы) для замены переменной значением 6.
|
Рассмотрим другой пример: 
Последнее уравнение (рисунок справа) условно эквивалентно уравнению: 2x=4. Решение уравнения Mathcad: 2. Формальное решение x = 2 не входит в область допустимых значений. Mathcad выдает правильное сообщение!
| 
|
| Здесь также правильное решение: множество решений совпадает с областью допустимых значений L = D. Только следует учесть, что D={R\{-1, 1}}.
|
| |
| | | |
Для численного решения линейных систем уравнений в MathCAD имеется специальная функция:
| lsolv(A, B) Она решает систему линейных алгебраических уравнений вида А x X =B, выдавая решение - вектор X. А - матрица коэффициентов размерности nxn; В - вектор свободных членов размерности n; X - вектор неизвестных пока решений.
|
| 
| Эквивалентной для MathCAD формой представления систем линейных уравнений является матричная форма. Представленные таким образом системы можно решать как символьно, так и численно.
|
Хорошей альтернативой решению систем в матричной форме является так
называемый solve block (Блок решения). Он удобен тем, что при его использовании уравнения записываются не в матричной, а в обычной форме, а также тем, что позволяет решать нелинейные уравнения и вводить ограничительные условия для определяемого решения. Блок решения применяется как для нахождения численного решения, так и для отыскания решеня в символьном виде.
Синтаксис Блока решения:
Given
Уравнения
Ограничительные условия
Find(v1, v2,...vn) - возвращает значение одной
или ряда переменных для точного решения
vi - переменные, которые надо найти.
Последовательность действий при численном решении:
| - Задаем начальные (стартовые) значения для искомых переменных.
- Заключаем уравнения в блок решения, начинающийся ключевым словом Given и заканчивающийся ключевым словом Find(v1, v2,...vn).
- Если после слова Find(v1, v2,...vn) ввести знак равенства [=], MathACD выдаст численное решение.
|
| При символьном решении не надо вводить начальные значения, а после ключевого слова Find(v1, v2,...vn) вместо знака равенства следует ввести символьный знак равенства (при помощи комбинации [Ctrl+.] или соответствующей пиктограммы панели Evaluation).
|
 
| Существует еще одно важное отличие между блоком решения и использованием матричных операций. Если определитель матрицы коэффициентов равен нулю, матричные методы оказываются непригодными. В таком случае система не имеет решений или разрешима неоднозначно. Если же применить блок решения, MathCAD распознает неоднозначность и выдает решение в параметрической форме. [4]
|
Многие уравнения, например трансцендентные, и системы из них не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью (не более значения, заданного системной переменной (TOL). Для простейших уравнений вида F(x)=0 решение находится с помощью функции
Rооt(Выражение, Имя_переменной)
Эта функция возвращает значение переменной с указанным уровнем точности, при котором выражение дает 0.
| Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно, если возможно несколько решений. Тогда выбор решения определяется выбором начального значения переменной. Пример ниже иллюстрирует технику применения функцииroot для вычисления корней кубического полинома.
|
| Как известно, кубическое уравнение обязательно имеет хотя бы один кубический корень х1. Он найден вначале функциейroot. Два других корня могут оказаться и комплексными. Функция root может отыскивать и такие корни. Для поиска второго корня, х2, первый исключается делением F(x) на (х-х1). Соответственно для поиска третьего корня, хЗ, F(X) делится еще и на (х-х2).
|
Эту процедуру можно распространить и на поиск корней полиномов более высокой степени, однако надо помнить, что найти корни полинома можно гораздо более изящным и простым способом - используя операцию символьных вычислений.
Популярное:
