Построение системы ОДУ для вероятностей состояний и среднего относительного числа заявок в системах сети
Рассмотрим замкнутую сеть массового обслуживания с разнотипными заявками, которая является вероятностной моделью обслуживания заявок в УП «Проектный институт Гродногипрозем», рис.1.1.
Рис.1.1. Модель обслуживания заявок в УП «Проектный институт Гродногипрозем».
Допустим, что  заявка типа
заявка типа 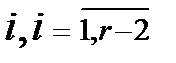 требуемой обслуживания,
требуемой обслуживания,  . Таким образом, в течение определенного интервала времени с требованиями по обслуживанию могут обращаться заявки
. Таким образом, в течение определенного интервала времени с требованиями по обслуживанию могут обращаться заявки 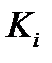 заявка типа
заявка типа 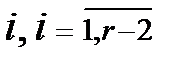 . Вначале все заявки поступают в систему
. Вначале все заявки поступают в систему  , которыми занимается
, которыми занимается  сотрудников. Заявки клиентов могут находиться в одном из следующих состояний:
сотрудников. Заявки клиентов могут находиться в одном из следующих состояний:  ― заявка не подается,
― заявка не подается,  ― заявка находится на стадии рассмотрения,
― заявка находится на стадии рассмотрения,  ― заявка находится на стадии выполнения. Переход заявки типа
― заявка находится на стадии выполнения. Переход заявки типа  из состояния
из состояния  в состояние
в состояние  происходит в случайные моменты времени, независимо от того в каком состоянии находятся другие заявки, и независимо от времени, таким образом, что вероятность перехода на интервале времени
происходит в случайные моменты времени, независимо от того в каком состоянии находятся другие заявки, и независимо от времени, таким образом, что вероятность перехода на интервале времени  равна
равна  , где
, где  - интенсивность такого перехода. Можно предположить, что интенсивность
- интенсивность такого перехода. Можно предположить, что интенсивность  является кусочно-постоянной функцией от времени с четырмя интервалами постоянства на отрезке времени
является кусочно-постоянной функцией от времени с четырмя интервалами постоянства на отрезке времени  :
:

где считаем, что  это количество недель за год. Так же учитывается время года: интенсивность потока заявок может быть различной взависимости от времени года. Будем предполагать, что наша система в некоторый момент находится в состоянии
это количество недель за год. Так же учитывается время года: интенсивность потока заявок может быть различной взависимости от времени года. Будем предполагать, что наша система в некоторый момент находится в состоянии

если в этот момент  заявка типа
заявка типа  находится в состояние
находится в состояние  ,
,  ― общее число заявок, находящихся в состоянии
― общее число заявок, находящихся в состоянии 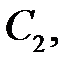 тогда
тогда  - число заявок в состоянии
- число заявок в состоянии 
Пусть, кроме того,  ― относительное число линий обслуживания заявки,
― относительное число линий обслуживания заявки,  ,
,  ― относительное число заявок,
― относительное число заявок,  , а
, а  среднее относительное число заявок, требующих обслуживания в каждой системе,
среднее относительное число заявок, требующих обслуживания в каждой системе,  .
.
Как указано выше, вероятностной моделью описанного выше обслуживания предприятия может служить замкнутая сеть массового обслуживания, состоящая из  систем обслуживания
систем обслуживания  с числом линий обслуживания соответственно
с числом линий обслуживания соответственно  и вероятностями перехода заявок
и вероятностями перехода заявок  ; в сети обслуживаются
; в сети обслуживаются 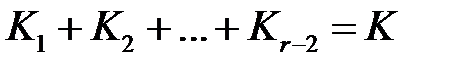 заявок типа
заявок типа  ; дисциплины обслуживания заявок в системах сети – FIFO. Для решения поставленной задачи необходимо, прежде всего, найти вектор среднего относительного числа единиц заявок, находящегося в состоянии
; дисциплины обслуживания заявок в системах сети – FIFO. Для решения поставленной задачи необходимо, прежде всего, найти вектор среднего относительного числа единиц заявок, находящегося в состоянии  в момент времени
в момент времени  :
:  Пусть
Пусть  интенсивность обслуживания заявок в каждой линии системы
интенсивность обслуживания заявок в каждой линии системы  . Состояние сети описывается вектором
. Состояние сети описывается вектором  где
где  число заявок находящихся в момент времени
число заявок находящихся в момент времени  в системе
в системе  .[1]
.[1]
Обозначим через 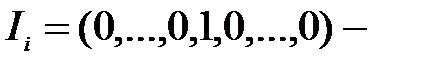
 - вектор с единицей на
- вектор с единицей на  ом месте. Очевидно, что
ом месте. Очевидно, что  . Случайный процесс
. Случайный процесс 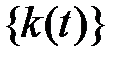 является марковским с непрерывным временем и дискретным множеством состояний, поскольку времена обслуживания заявок в системах сети распределены по показательному закону. Возможны следующие переходы в состояние
является марковским с непрерывным временем и дискретным множеством состояний, поскольку времена обслуживания заявок в системах сети распределены по показательному закону. Возможны следующие переходы в состояние 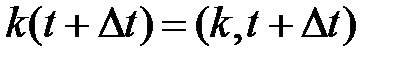 за время
за время 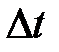 для этого процесса:
для этого процесса:
из состояния  с вероятностью
с вероятностью

из состояния  с вероятностью
с вероятностью

из состояния  с вероятностью
с вероятностью
 ;
;
из состояния  с вероятностью
с вероятностью

из состояния  с вероятностью
с вероятностью

из остальных состояний с вероятностью  .
.
Тогда, используя формулу полной вероятности, можно записать систему разностных уравнений:
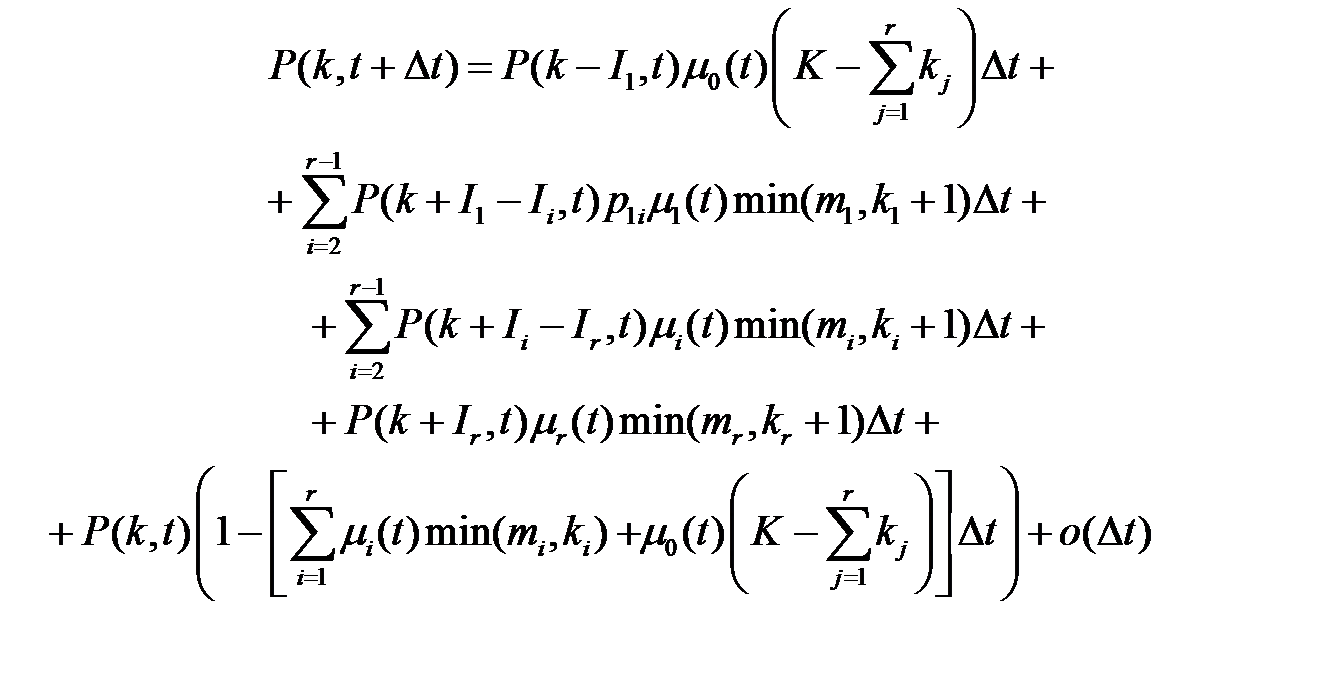
Переходя к пределу при  , получим систему разностно-дифференциальных уравнений Колмогорова для вероятностей состояний,
, получим систему разностно-дифференциальных уравнений Колмогорова для вероятностей состояний,

которая может быть представлена в виде
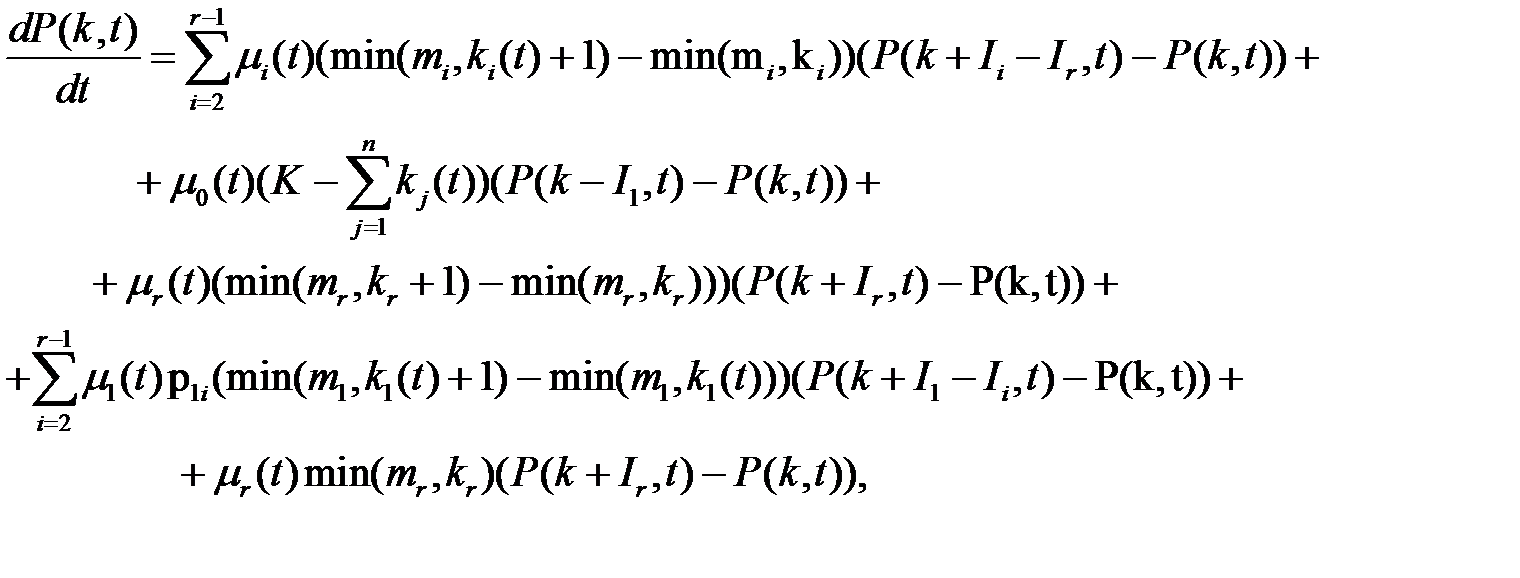
 (1.1)
(1.1)
Решение этой системы в аналитическом виде в общем случае затруднительно. В связи с этим рассмотрим важный случай большого числа исков, когда 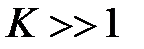 . Чтобы найти распределения вероятностей случайного вектора
. Чтобы найти распределения вероятностей случайного вектора  удобно перейти к относительным переменным, рассматривая вектор
удобно перейти к относительным переменным, рассматривая вектор  В этом случае возможные значения этого вектора при фиксированном
В этом случае возможные значения этого вектора при фиксированном 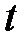 принадлежат ограниченному замкнутому множеству
принадлежат ограниченному замкнутому множеству

в котором они располагаются в узлах  мерной решетки на расстоянии
мерной решетки на расстоянии  друг от друга. При увеличении
друг от друга. При увеличении  " плотность заполнения" множества
" плотность заполнения" множества  возможными компонентами рассматриваемого вектора увеличивается и становится возможным считать, что он имеет непрерывное распределение с плотностью вероятностей
возможными компонентами рассматриваемого вектора увеличивается и становится возможным считать, что он имеет непрерывное распределение с плотностью вероятностей  где
где  имеет смысл плотности вероятностей случайного вектора
имеет смысл плотности вероятностей случайного вектора  .
.
Обозначим через 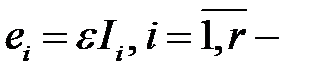 вектор с компонентами равными нулю за исключением
вектор с компонентами равными нулю за исключением  ой,
ой,

Заметим, что
 (1.2)
(1.2)
 (1.3)
(1.3)
Переписывая систему уравнений (1.1) для плотности  , получим
, получим
 (1.4)
(1.4)
где  Представим правую часть этой системы уравнений с точностью до членов порядка малости
Представим правую часть этой системы уравнений с точностью до членов порядка малости  Если
Если  дважды дифференцируема по
дважды дифференцируема по 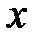 , то справедливы соотношения
, то справедливы соотношения

Использую и то, что  , систему уравнений (1.4) можно преобразовать к виду:
, систему уравнений (1.4) можно преобразовать к виду:

Введем следующие функции [2]
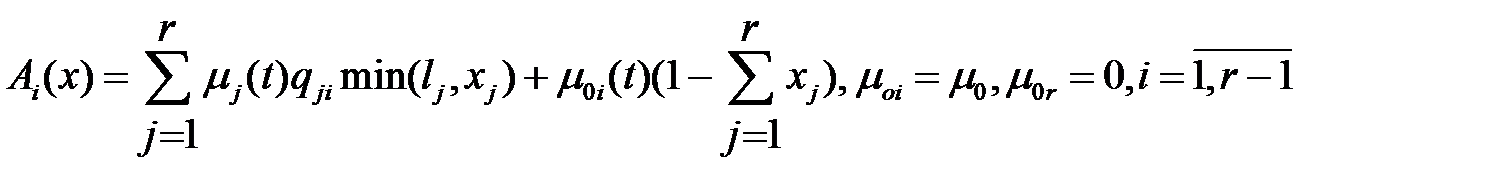

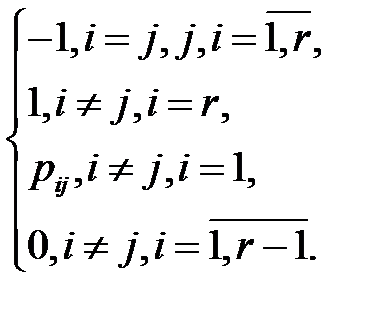

Тогда система уравнений (1.7) имеет вид
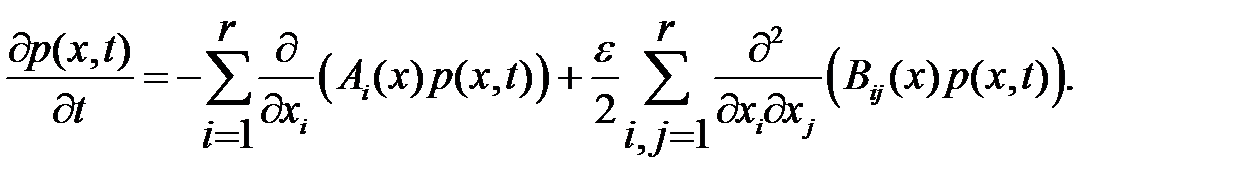
Таким образом, плотность  удовлетворяет с точностью до членов порядка
удовлетворяет с точностью до членов порядка  системе уравнений Колмогорова-Фоккера-Планка. Отсюда следует, что математические ожидания
системе уравнений Колмогорова-Фоккера-Планка. Отсюда следует, что математические ожидания 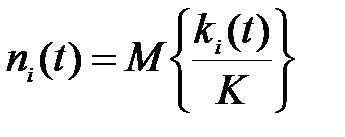 с точностью
с точностью  определяются из системы уравнений
определяются из системы уравнений
 (1.5)
(1.5)
Правые части уравнений (1.5) являются кусочно-линейными функциями. Определим явную форму уравнений (1.5) в областях линейности их правых частей. Пусть  множество индексов компонент вектора
множество индексов компонент вектора  Разобьем
Разобьем 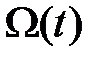 на два непересекающихся множества
на два непересекающихся множества 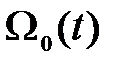 и
и  следующим образом.
следующим образом.


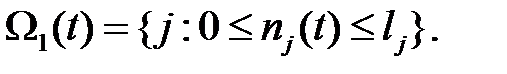
При фиксированном 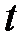 число разбиений такого рода равно
число разбиений такого рода равно  Каждое разбиение будет задавать в множестве
Каждое разбиение будет задавать в множестве  непересекающиеся области
непересекающиеся области  такие, что
такие, что



Теперь можно записать систему уравнений (1.5) в явной форме для каждой из областей  :
:
 , (1.6)
, (1.6)
где 

В общем случае система уравнений (1.6) в области  записывается в виде
записывается в виде

С учетом того, что  ,
,  ,
,  и
и 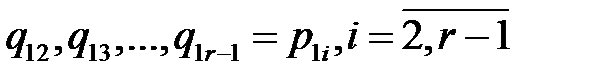 , остальные
, остальные 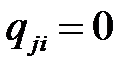 , то она примет вид
, то она примет вид

Решение последней системы при произвольном 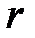 затруднительно
затруднительно
Популярное:

