Методика расчета фильтрационного сопротивления, при притоке жидкости к несовершенной скважине по линейному закону фильтрации
Приток жидкости к скважине определяется формулой Дюпюи:
 , (2.1) , (2.1)
где Q – объемный дебит жидкости, м3/с; k – коэффициент проницаемости, м2;
h – эффективная нефтенасыщенная толщина пласта, м; 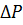 – разность давления, Па; μ – динамическая вязкость, Па· с; R0 – радиус контура питания скважины, м; rc – радиус скважины, м; – разность давления, Па; μ – динамическая вязкость, Па· с; R0 – радиус контура питания скважины, м; rc – радиус скважины, м;
Любое решение для притока жидкости к несовершенной скважине
(рис. 2.1) можно представить обобщенной формулой Дюпюи, введя дополнительные фильтрационные сопротивления [4, 21].

Рис. 2.1. Схема притока к несовершенной скважине в ограниченном однородно-анизотропном пласте
Задача о притоке жидкости к несовершенной по степени вскрытия скважине в пласте конечной толщины h0 исследовалась М. Маскетом [1]. Вдоль оси скважины на вскрытой части длиной b он располагал воображаемую линию, поглощающую жидкость, каждый элемент которой является стоком. Подбирая интенсивность расходов, и используя метод суперпозиции действительных и отображённых стоков, М. Маскет получил следующую формулу для дебита гидродинамически несовершенной по степени вскрытия пласта скважины:
 , (2.2) , (2.2)
где
 (2.3) (2.3)
есть функция фильтрационного сопротивления.
Функция 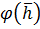 имеет следующее аналитическое выражение: имеет следующее аналитическое выражение:
 , (2.4) , (2.4)
где  – гамма функция Эйлера. Гамма функция Эйлера раскладывается в ряд следующим образом: – гамма функция Эйлера. Гамма функция Эйлера раскладывается в ряд следующим образом:
 . (2.5) . (2.5)
А.П. Телков на основе решения Стклянина-Телкова [7] для потенциала несовершенной скважины
 , (2.6) , (2.6)
где  – эксцентриситет; – эксцентриситет;  – потенциал скорости фильтрации на контуре питания; – потенциал скорости фильтрации на контуре питания; 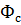 – потенциал скорости фильтрации на контуре скважины. – потенциал скорости фильтрации на контуре скважины.
Получил выражение для расчета фильтрационного сопротивления:
 , (2.7) , (2.7)
в котором функция  определяется как: определяется как:
 ; (2.8) ; (2.8)
где 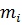 – положительный корень уравнения – положительный корень уравнения  ; ;  – функция Бесселя первого рода нулевого порядка; – функция Бесселя первого рода нулевого порядка;  – функция Бесселя первого рода первого порядка; – функция Бесселя первого рода первого порядка; 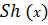 – гиперболический синус; – гиперболический синус;  – относительное вскрытие пласта; – относительное вскрытие пласта;  - безразмерный параметр, определяемый по следующей формуле: - безразмерный параметр, определяемый по следующей формуле:
 . (2.9) . (2.9)
2.1.1 Анализ функции 
Для расчета сложной функции  , которая была аналитически выведена Ю.И. Сткляниным и А.П. Телковым [7] и используется во многих решениях, при нахождении фильтрационных сопротивлений по линейному закону фильтрации, поэтому необходимо ее подробно рассмотреть. Функция , которая была аналитически выведена Ю.И. Сткляниным и А.П. Телковым [7] и используется во многих решениях, при нахождении фильтрационных сопротивлений по линейному закону фильтрации, поэтому необходимо ее подробно рассмотреть. Функция  включает в себя гиперболическую функцию синуса включает в себя гиперболическую функцию синуса  , специальные функции, такие как функция Бесселя 1-го рода нулевого порядка , специальные функции, такие как функция Бесселя 1-го рода нулевого порядка  и функция Бесселя 1-го рода первого порядка и функция Бесселя 1-го рода первого порядка  , и ряд суммы от 1 до ∞. , и ряд суммы от 1 до ∞.
Графическое изображение функций 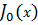 и и  для для  от 0 до 100 представлено на рис. 2.2. от 0 до 100 представлено на рис. 2.2.

Рис. 2.2. Функции Бесселя первого рода нулевого  и первого и первого  порядка порядка
Был разработан программный продукт для расчета функции  . Для нахождения корней функции Бесселя 1-го рода нулевого порядка . Для нахождения корней функции Бесселя 1-го рода нулевого порядка  алгоритм [22]. алгоритм [22].
Таблица 2.1 – Первые 100 положительных корней уравнения 
| Положительные корни уравнения J0(μ i)=0
| | μ 1
| 2, 4048256
| μ 26
| 80, 8975559
| μ 51
| 159, 4366112
| μ 76
| 237, 9761688
| | μ 2
| 5, 5200781
| μ 27
| 84, 0390908
| μ 52
| 162, 5781887
| μ 77
| 241, 1177546
| | μ 3
| 8, 6537279
| μ 28
| 87, 1806298
| μ 53
| 165, 7197667
| μ 78
| 244, 2593406
| | μ 4
| 11, 7915344
| μ 29
| 90, 3221726
| μ 54
| 168, 8613454
| μ 79
| 247, 4009267
| | μ 5
| 14, 9309177
| μ 30
| 93, 4637188
| μ 55
| 172, 0029245
| μ 80
| 250, 5425130
| | μ 6
| 18, 0710640
| μ 31
| 96, 6052680
| μ 56
| 175, 1445041
| μ 81
| 253, 6840995
| | μ 7
| 21, 2116366
| μ 32
| 99, 7468199
| μ 57
| 178, 2860842
| μ 82
| 256, 8256861
| | μ 8
| 24, 3524715
| μ 33
| 102, 8883743
| μ 58
| 181, 4276647
| μ 83
| 259, 9672729
| | μ 9
| 27, 4934791
| μ 34
| 106, 0299309
| μ 59
| 184, 5692456
| μ 84
| 263, 1088598
| | μ 10
| 30, 6346065
| μ 35
| 109, 1714896
| μ 60
| 187, 7108270
| μ 85
| 266, 2504469
| | μ 11
| 33, 7758202
| μ 36
| 112, 3130503
| μ 61
| 190, 8524087
| μ 86
| 269, 3920340
| | μ 12
| 36, 9170984
| μ 37
| 115, 4546127
| μ 62
| 193, 9939907
| μ 87
| 272, 5336214
| | μ 13
| 40, 0584258
| μ 38
| 118, 5961766
| μ 63
| 197, 1355731
| μ 88
| 275, 6752088
| | μ 14
| 43, 1997917
| μ 39
| 121, 7377421
| μ 64
| 200, 2771558
| μ 89
| 278, 8167963
| | μ 15
| 46, 3411884
| μ 40
| 124, 8793089
| μ 65
| 203, 4187388
| μ 90
| 281, 9583840
| | μ 16
| 49, 4826099
| μ 41
| 128, 0208770
| μ 66
| 206, 5603221
| μ 91
| 285, 0999717
| | μ 17
| 52, 6240518
| μ 42
| 131, 1624463
| μ 67
| 209, 7019057
| μ 92
| 288, 2415596
| | μ 18
| 55, 7655108
| μ 43
| 134, 3040166
| μ 68
| 212, 8434896
| μ 93
| 291, 3831474
| | μ 19
| 58, 9069839
| μ 44
| 137, 4455880
| μ 69
| 215, 9850736
| μ 94
| 294, 5247357
| | μ 20
| 62, 0484692
| μ 45
| 140, 5871604
| μ 70
| 219, 1266580
| μ 95
| 297, 6663239
| | μ 21
| 65, 1899648
| μ 46
| 143, 7287336
| μ 71
| 222, 2682426
| μ 96
| 300, 8079121
| | μ 22
| 68, 3314693
| μ 47
| 146, 8703076
| μ 72
| 225, 4098274
| μ 97
| 303, 9495005
| | μ 23
| 71, 4729816
| μ 48
| 150, 0118825
| μ 73
| 228, 5514125
| μ 98
| 307, 0910889
| | μ 24
| 74, 6145006
| μ 49
| 153, 1534580
| μ 74
| 231, 6929977
| μ 99
| 310, 2326775
| | μ 25
| 77, 7560256
| μ 50
| 156, 2950343
| μ 75
| 234, 8345831
| μ 100
| 313, 3742661
|
Переход для функций Бесселя первого рода к интегральному виду осуществляется по формуле:
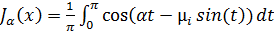 . (2.11) . (2.11)
Для вычисления значений функции 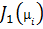 , функция Бесселя первого рода первого порядка была представлена интегралом Бесселя: , функция Бесселя первого рода первого порядка была представлена интегралом Бесселя:
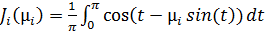 ; (2.12) ; (2.12)
Интеграл (2.12) вычислялся приближенно методом Симпсона [23], по алгоритму [22], с точностью  . Результаты расчета затабулированы и представлены в табл. 2.2. . Результаты расчета затабулированы и представлены в табл. 2.2.
Таблица 2.2 – Значения функции Бесселя первого рода первого порядка J1(mi)
| Значения функции J1(μ i)
| | i
| J1(μ i)
| i
| J1(μ i)
| i
| J1(μ i)
| i
| J1(μ i)
| |
| 0, 5191475
|
| -0, 0887108
|
| 0, 0631898
|
| -0, 0517218
| |
| -0, 3402648
|
| 0, 0870369
|
| -0, 0625763
|
| 0, 0513838
| |
| 0, 2714523
|
| -0, 0854542
|
| 0, 0619803
|
| -0, 0510523
| |
| -0, 2324598
|
| 0, 0839549
|
| -0, 0614011
|
| 0, 0507271
| |
| 0, 2065464
|
| -0, 0825319
|
| 0, 0608377
|
| -0, 0504080
| |
| -0, 1877288
|
| 0, 0811788
|
| -0, 0602896
|
| 0, 0500949
| |
| 0, 1732659
|
| -0, 0798902
|
| 0, 0597561
|
| -0, 0497876
| |
| -0, 1617015
|
| 0, 0786610
|
| -0, 0592365
|
| 0, 0494859
| |
| 0, 1521812
|
| -0, 0774869
|
| 0, 0587302
|
| -0, 0491895
| |
| -0, 1441810
|
| 0, 0763638
|
| -0, 0582366
|
| 0, 0488985
| |
| 0, 1372969
|
| -0, 0752882
|
| 0, 0577553
|
| -0, 0486125
| |
| -0, 1313246
|
| 0, 0742568
|
| -0, 0572858
|
| 0, 0483315
| |
| 0, 1260695
|
| -0, 0732667
|
| 0, 0568275
|
| -0, 0480553
| |
| -0, 1213986
|
| 0, 0723151
|
| -0, 0563800
|
| 0, 0477838
| |
| 0, 1172112
|
| -0, 0713997
|
| 0, 0559429
|
| -0, 0475169
| |
| -0, 1134292
|
| 0, 0705182
|
| -0, 0555159
|
| 0, 0472544
| |
| 0, 1099911
|
| -0, 0696686
|
| 0, 0550985
|
| -0, 0469961
| |
| -0, 1068479
|
| 0, 0688489
|
| -0, 0546903
|
| 0, 0467421
| |
| 0, 1039596
|
| -0, 0680575
|
| 0, 0542911
|
| -0, 0464921
| |
| -0, 1012935
|
| 0, 0672928
|
| -0, 0539005
|
| 0, 0462461
| |
| 0, 0988226
|
| -0, 0665533
|
| 0, 0535182
|
| -0, 0460040
| |
| -0, 0965240
|
| 0, 0658376
|
| -0, 0531440
|
| 0, 0457657
| |
| 0, 0943788
|
| -0, 0651446
|
| 0, 0527775
|
| -0, 0455310
| |
| -0, 0923705
|
| 0, 0644730
|
| -0, 0524184
|
| 0, 0452998
| |
| 0, 0904852
|
| -0, 0638217
|
| 0, 0520666
|
| -0, 0450722
|
Преобразуем формулу (2.8) для расчета. Для этого нужно избавиться от бесконечности в верхнем пределе суммы, заменив ее на целое число N. N определяется из следующего неравенства:
 , (2.13) , (2.13)
где 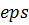 – точность расчета ряда суммы. Здесь она принимается 10-5. Такую точность обеспечивает N≈ 100. – точность расчета ряда суммы. Здесь она принимается 10-5. Такую точность обеспечивает N≈ 100.
А.П. Телковым [4, 21] для нахождения значения  предложены табулированные значения предложены табулированные значения  в диапазоне в диапазоне  и и
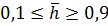 с достаточно большим шагом (табл. 2.3), и графическая зависимость функции с достаточно большим шагом (табл. 2.3), и графическая зависимость функции  (рис. 2.3), которые используются для определения коэффициентов дополнительного фильтрационного сопротивления в работах автора. Номограмма, представляющая функцию (рис. 2.3), которые используются для определения коэффициентов дополнительного фильтрационного сопротивления в работах автора. Номограмма, представляющая функцию  графически, имеет ограниченное количество кривых для графически, имеет ограниченное количество кривых для  , что не позволяет проводить расчеты в широком диапазоне переменных данных. , что не позволяет проводить расчеты в широком диапазоне переменных данных.
Сопоставим результаты полученные по формуле
 (2.14) (2.14)
с табличными данным А.П. Телкова. Так для 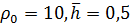 значение значение 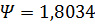 по формуле, а из таблицы находим по формуле, а из таблицы находим  . При . При  значения значения 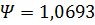 , и , и  по формуле и таблице соответственно. Занижение примерно на 3% справедливо для всех по формуле и таблице соответственно. Занижение примерно на 3% справедливо для всех  представленных в таблице. Это объясняется тем, что табулированные данные были вычислены для N=40. Значение N было установлено методом перебора (равномерного поиска). Для N=40, представленных в таблице. Это объясняется тем, что табулированные данные были вычислены для N=40. Значение N было установлено методом перебора (равномерного поиска). Для N=40, 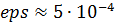 , а так как значения под знаком суммы положительны при любом , а так как значения под знаком суммы положительны при любом 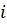 , то эту разницу будет составлять , то эту разницу будет составлять
 . (2.15) . (2.15)
Подводя итоги вышеизложенному, следует отметить, что затабулированные в работе [4] значения функции  рассчитаны до сорокового члена ряда суммы и обеспечивают удовлетворительную точность расчетов, но современная компьютерная техника позволяет производить более точные вычисления. Так приняв количество членов ряда суммы рассчитаны до сорокового члена ряда суммы и обеспечивают удовлетворительную точность расчетов, но современная компьютерная техника позволяет производить более точные вычисления. Так приняв количество членов ряда суммы  , получим более высокую точность расчетов, и отличие от значений в табл 2.3 на 3% в большую сторону. , получим более высокую точность расчетов, и отличие от значений в табл 2.3 на 3% в большую сторону.
Таблица 2.3 – Табулированные значения функции 

| 0, 1
| 0, 2
| 0, 3
| 0, 4
| 0, 5
| 0, 6
| 0, 7
| 0, 8
| 0, 9
| | 0, 1
| 0, 3552
| 0, 1787
| 0, 1191
| 0, 0893
| 0, 0715
| 0, 0596
| 0, 0511
| 0, 0447
| 0, 0395
| | 0, 111
| 0, 3928
| 0, 1983
| 0, 1322
| 0, 0992
| 0, 0793
| 0, 0661
| 0, 0567
| 0, 0496
| 0, 0436
| | 0, 125
| 0, 4456
| 0, 2263
| 0, 1509
| 0, 1132
| 0, 0906
| 0, 0647
| 0, 0647
| 0, 0566
| 0, 0495
| | 0, 143
| 0, 5097
| 0, 2612
| 0, 1743
| 0, 1307
| 0, 1046
| 0, 0872
| 0, 0747
| 0, 0653
| 0, 0566
| | 0, 167
| 0, 59
| 0, 3069
| 0, 205
| 0, 1538
| 0, 123
| 0, 1025
| 0, 0879
| 0, 0767
| 0, 0656
| | 0, 2
| 0, 6956
| 0, 3699
| 0, 2479
| 0, 186
| 0, 1488
| 0, 124
| 0, 1063
| 0, 0925
| 0, 0773
| | 0, 25
| 0, 8376
| 0, 4612
| 0, 3115
| 0, 2341
| 0, 1873
| 0, 156
| 0, 1335
| 0, 1135
| 0, 0931
| | 0, 3
| 0, 98
| 0, 557
| 0, 382
| 0, 287
| 0, 23
| 0, 192
| 0, 164
| 0, 139
| 0, 109
| | 0, 333
| 1, 0373
| 0, 6004
| 0, 4125
| 0, 3115
| 0, 2495
| 0, 2077
| 0, 1768
| 0, 1501
| 0, 1153
| | 0, 4
| 1, 204
| 0, 72
| 0, 503
| 0, 383
| 0, 304
| 0, 255
| 0, 216
| 0, 18
| 0, 134
| | 0, 5
| 1, 3646
| 0, 854
| 0, 6101
| 0, 4685
| 0, 377
| 0, 3123
| 0, 2615
| 0, 2135
| 0, 1516
| | 0, 6
| 1, 525
| 0, 947
| 0, 717
| 0, 557
| 0, 45
| 0, 371
| 0, 308
| 0, 246
| 0, 17
| | 0, 7
| 1, 653
| 1, 097
| 0, 81
| 0, 585
| 0, 516
| 0, 424
| 0, 349
| 0, 274
| 0, 183
| | 0, 8
| 1, 8
| 1, 213
| 0, 91
| 0, 713
| 0, 58
| 0, 476
| 0, 39
| 0, 303
| 0, 2
| | 0, 9
| 1, 873
| 1, 287
| 0, 975
| 0, 773
| 0, 628
| 0, 515
| 0, 418
| 0, 322
| 0, 208
| |
| 1, 9585
| 1, 3654
| 1, 044
| 0, 8326
| 0, 6781
| 0, 5551
| 0, 4474
| 0, 4314
| 0, 2176
| |
| 2, 54
| 1, 9
| 1, 515
| 1, 24
| 1, 015
| 0, 823
| 0, 65
| 0, 475
| 0, 282
| |
| 3, 09
| 2, 45
| 1, 975
| 1, 632
| 1, 345
| 1, 05
| 0, 845
| 0, 603
| 0, 343
| |
| 3, 68
| 3, 03
| 2, 535
| 2, 123
| 1, 756
| 1, 415
| 1, 09
| 0, 757
| 0, 4
| |
| 4, 181
| 3, 67
| 3, 184
| 2, 715
| 2, 259
| 1, 81
| 1, 365
| 0, 918
| 0, 465
| |
| 4, 251
| 3, 779
| 3, 306
| 2, 834
| 2, 362
| 1, 889
| 1, 417
| 0, 945
| 0, 472
| 
Рис. 2.3. Графическое изображение функции 
Популярное:
|

