В чём заключается релятивистская трактовка магнитных явлений?
2) Сформулировать закон Био-Савара; закон Ампера. Био и Савар провели в 1820 г. исследование магнитных полей, текущих по тонким проводам различной формы. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками токов. Для магнитной индукции поля, создаваемого элементом тока длины dl, Лаплас получил формулу 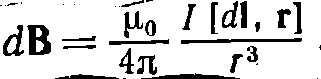 В связи с этим соотношение носит название закона Био — Савара — Лапласа или более кратко закона Био — Савара. Из рис. 42.1 видно, что вектор dB направлен перпендикулярно к
В связи с этим соотношение носит название закона Био — Савара — Лапласа или более кратко закона Био — Савара. Из рис. 42.1 видно, что вектор dB направлен перпендикулярно к
плоскости, проходящей через dl и точку, в которой вычисляется поле, причем так, что вращение вокруг dl в направлении dB связано с dl правилом правого винта. Модуль dB определяется выражением 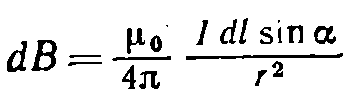 где а — угол между векторами dl и г. Применим формулу
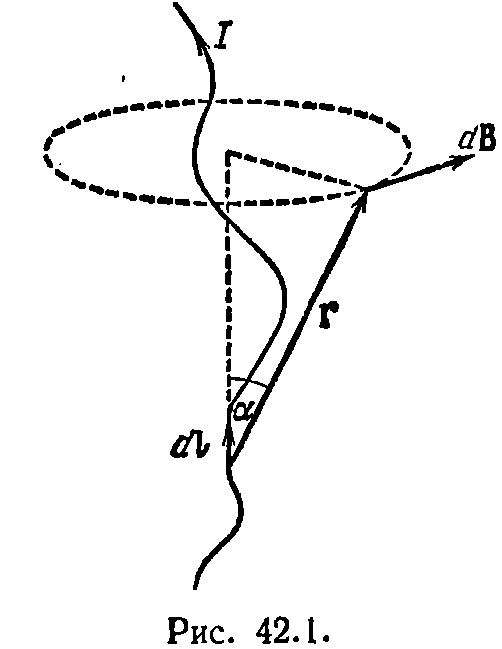
где а — угол между векторами dl и г. Применим формулу 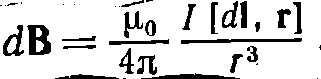 для вычисления поля прямого тока, т. е. поля, создаваемого током, текущим по тонкому прямому проводу бесконечной длины (рис. 42.2). Все векторы dB в данной точке имеют одинаковое направление (в нашем случае за чертеж). Поэтому сложение векторов dB можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рис. 42.2 видно, что
для вычисления поля прямого тока, т. е. поля, создаваемого током, текущим по тонкому прямому проводу бесконечной длины (рис. 42.2). Все векторы dB в данной точке имеют одинаковое направление (в нашем случае за чертеж). Поэтому сложение векторов dB можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рис. 42.2 видно, что 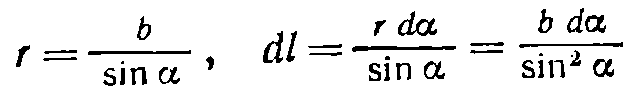 Подставим эти значения в формулу:
Подставим эти значения в формулу: 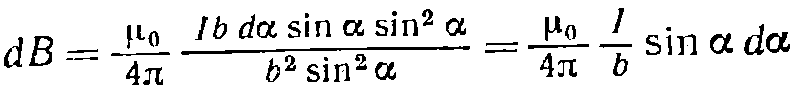
Угол a для всех элементов бесконечного прямого тока изменяется в пределах от 0 до π. Следовательно, 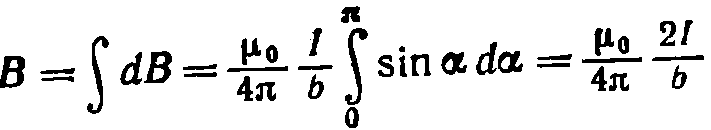 Таким образом, магнитная индукция поля прямого тока определяется формулой
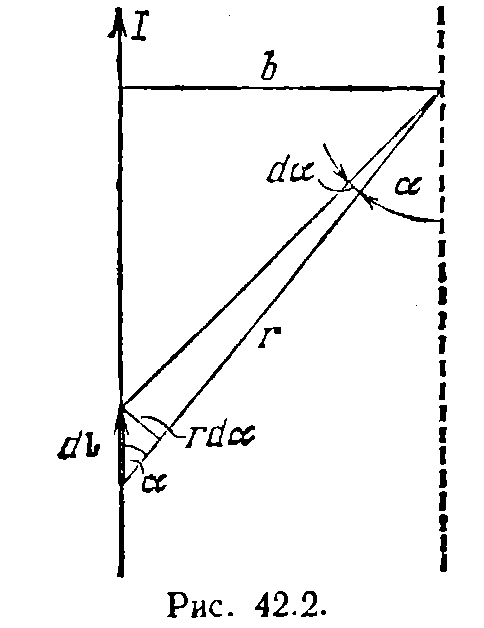
Таким образом, магнитная индукция поля прямого тока определяется формулой 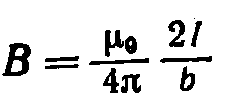 . Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей (рис. 42.3).
. Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей (рис. 42.3).
Закон Ампера: Если провод, по которому течет ток, находится в магнитном поле, на каждый из носителей тока действует сила 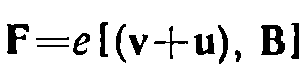 Здесь v — скорость хаотического движения носителя, u — скорость упорядоченного движения. От носителя тока действие этой силы передается проводнику, по которому он перемещается. В результате на провод с током, находящийся в магнитном поле, действует сила. Найдем величину силы dF, действующей на элемент провода длины dl. Усредним выражение
Здесь v — скорость хаотического движения носителя, u — скорость упорядоченного движения. От носителя тока действие этой силы передается проводнику, по которому он перемещается. В результате на провод с током, находящийся в магнитном поле, действует сила. Найдем величину силы dF, действующей на элемент провода длины dl. Усредним выражение 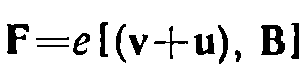 по носителям тока, содержащимся в элементе dl:
по носителям тока, содержащимся в элементе dl: 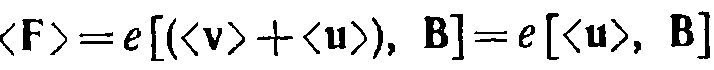 (В — магнитная индукция в том месте, где помещается элемент dl). В элементе провода содержится число носителей, равное nS dl( n— число носителей в единице объема, S — площадь поперечного сечения провода в данном месте).
(В — магнитная индукция в том месте, где помещается элемент dl). В элементе провода содержится число носителей, равное nS dl( n— число носителей в единице объема, S — площадь поперечного сечения провода в данном месте). 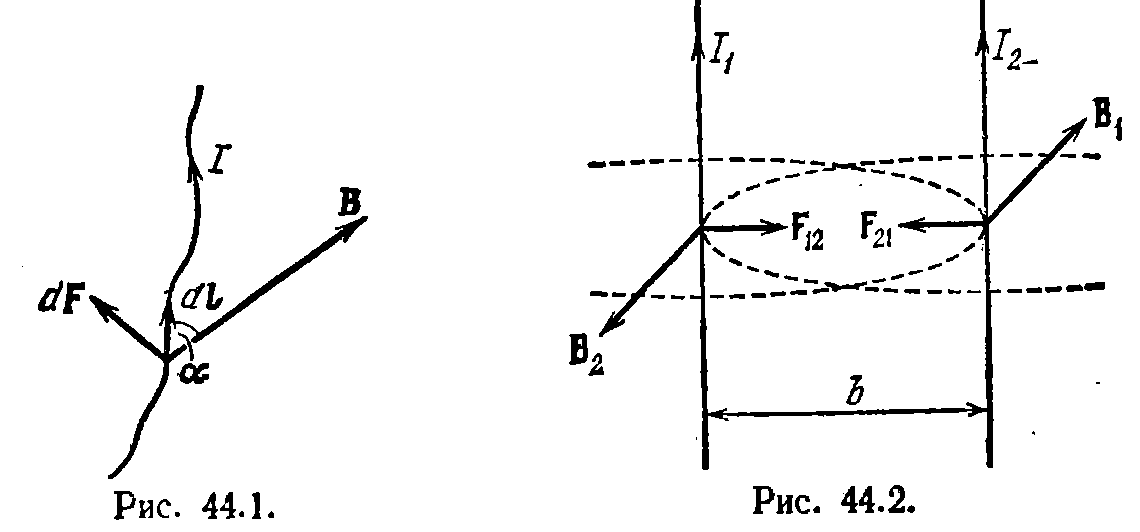 Умножив выражение на число носителей, найдем интересующую нас силу:
Умножив выражение на число носителей, найдем интересующую нас силу: 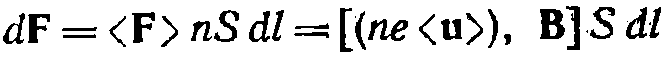
Приняв во внимание, что nl< u> есть плотность тока j, a S dl дает объем элемента провода dV, можно написать 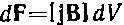 Отсюда можно получить выражение для плотности силы, т. е. для силы, действующей на единицу объема проводника:
Отсюда можно получить выражение для плотности силы, т. е. для силы, действующей на единицу объема проводника: 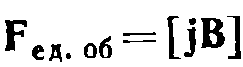 Напишем формулу в виде
Напишем формулу в виде 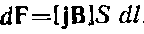 Заменив S dl через jS dl=I dl, придем к формуле
Заменив S dl через jS dl=I dl, придем к формуле 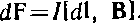 Эта формула определяет силу, действующую на элемент тока dl в магнитном поле. Соотношение было установлено экспериментально Ампером и носит название закона Ампера. Мы получили закон Ампера, исходя из выражения для магнитной силы. В действительности выражение для магнитной силы было получено из установленного экспериментально соотношения
Эта формула определяет силу, действующую на элемент тока dl в магнитном поле. Соотношение было установлено экспериментально Ампером и носит название закона Ампера. Мы получили закон Ампера, исходя из выражения для магнитной силы. В действительности выражение для магнитной силы было получено из установленного экспериментально соотношения 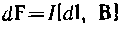 Модуль силы вычисляется по формуле
Модуль силы вычисляется по формуле 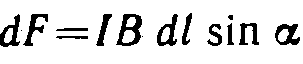 где а — угол между векторами dl и В (рис. 44.1). Направлена сила перпендикулярно к плоскости, в которой лежат векторы dl и В. Применим закон Ампера для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами Ь (рис. 44.2), то каждый элемент тока l2 будет находиться в магнитном поле, индукция которого равна
где а — угол между векторами dl и В (рис. 44.1). Направлена сила перпендикулярно к плоскости, в которой лежат векторы dl и В. Применим закон Ампера для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами Ь (рис. 44.2), то каждый элемент тока l2 будет находиться в магнитном поле, индукция которого равна 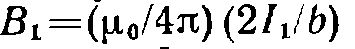 Угол а между элементами тока l2 и вектором В прямой. Следовательно, на единицу длины тока l2 действует сила
Угол а между элементами тока l2 и вектором В прямой. Следовательно, на единицу длины тока l2 действует сила 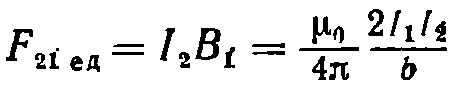 Для силы F. действующей на единицу длины тока l1, получается аналогичное выражение. Легко убедиться в том, что при одинаковом направлении токов они притягивают друг друга, а при различном — отталкивают.
Для силы F. действующей на единицу длины тока l1, получается аналогичное выражение. Легко убедиться в том, что при одинаковом направлении токов они притягивают друг друга, а при различном — отталкивают.
3) Записать выражение для силы Лоренца. На заряд, движущийся в магнитном поле, действует сила, которую мы будем называть магнитной. Эта сила определяется зарядом q, скоростью его движения v и магнитной индукцией В в той точке, где находится заряд в рассматриваемый момент времени. Простейшее предположение заключается в том, что модуль силы F пропорционален каждой из трех величин q, v и В. Кроме того, можно ожидать, что F зависит от взаимной ориентации векторов v и В. Направление вектора F должно определяться направлениями векторов v и В. Для того, чтобы «сконструировать» вектор F из скаляра q и векторов v и В, перемножим v и В векторно и умножим затем получившийся результат на скаляр q. В итоге получим выражение 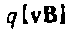 Опытным путем установлено, что сила F, действующая на заряд, движущийся в магнитном поле, определяется формулой
Опытным путем установлено, что сила F, действующая на заряд, движущийся в магнитном поле, определяется формулой 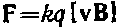 где к — коэффициент пропорциональности, зависящий от выбора единиц фигурирующих в формуле величин. Эти рассуждения не носят доказательной силы. Их назначение состоит в том, чтобы облегчить запоминание формулы. Справедливость же этой формулы может быть установлена только экспериментально. Отметим, что соотношение
где к — коэффициент пропорциональности, зависящий от выбора единиц фигурирующих в формуле величин. Эти рассуждения не носят доказательной силы. Их назначение состоит в том, чтобы облегчить запоминание формулы. Справедливость же этой формулы может быть установлена только экспериментально. Отметим, что соотношение 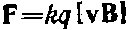 можно рассматривать как определение магнитной индукции В. Единица магнитной индукции В — тесла — определяется так, чтобы коэффициент пропорциональности к в формуле был равен единице. Следовательно, в СИ эта формула имеет вид
можно рассматривать как определение магнитной индукции В. Единица магнитной индукции В — тесла — определяется так, чтобы коэффициент пропорциональности к в формуле был равен единице. Следовательно, в СИ эта формула имеет вид 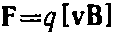 Модуль магнитной силы равен
Модуль магнитной силы равен 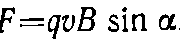 где а — угол между векторами v и В. вытекает, что заряд, движущийся вдоль линий магнитного поля, не испытывает действия магнитной силы. Направлена магнитная сила перпендикулярно к плоскости, в которой лежат векторы v и В. Если заряд q положителен, направление силы совпадает с направлением вектора [vB]. В случае отрицательного q направления векторов F и [vB] противоположны (рис. 43.1).
где а — угол между векторами v и В. вытекает, что заряд, движущийся вдоль линий магнитного поля, не испытывает действия магнитной силы. Направлена магнитная сила перпендикулярно к плоскости, в которой лежат векторы v и В. Если заряд q положителен, направление силы совпадает с направлением вектора [vB]. В случае отрицательного q направления векторов F и [vB] противоположны (рис. 43.1). 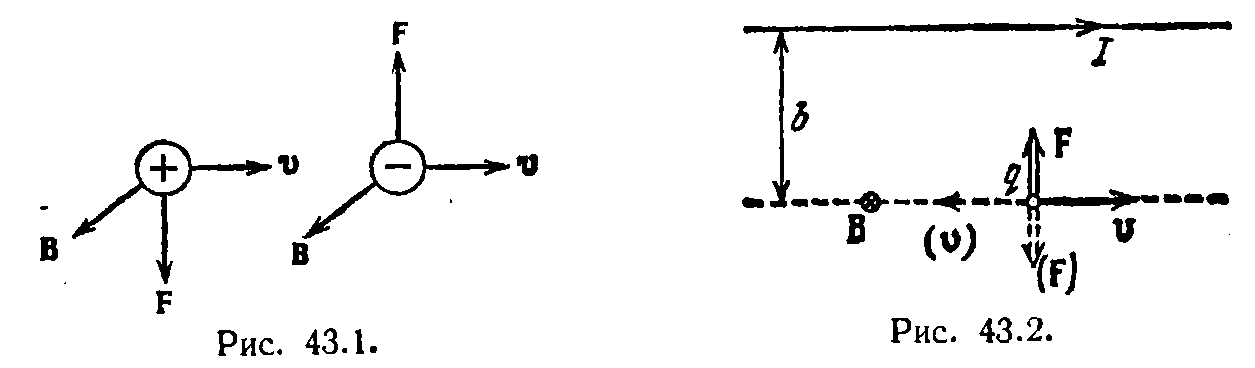 Поскольку магнитная сила всегда направлена перпендикулярно к скорости заряженной частицы, она работы над частицей не совершает. Следовательно, действуя на заряженную частицу постоянным магнитным полем, изменить ее энергию нельзя. Если имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна
Поскольку магнитная сила всегда направлена перпендикулярно к скорости заряженной частицы, она работы над частицей не совершает. Следовательно, действуя на заряженную частицу постоянным магнитным полем, изменить ее энергию нельзя. Если имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна  . Это выражение было получено из опыта Лоренцем и носит название силы Лоренца или лоренцевой силы.
. Это выражение было получено из опыта Лоренцем и носит название силы Лоренца или лоренцевой силы.
Пусть заряд q движется со скоростью v параллельно прямому бесконечному проводу, по которому течет ток силы I (рис. 43.2). Согласно формулам на заряд действует в этом случае магнитная сила, равная по модулю 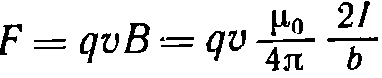 где b — расстояние от заряда до провода. В случае положительного заряда сила направлена к проводу, если направления тока и движения заряда одинаковы, и от провода, если направления тока и движения заряда противоположны (см. рис. 43.2). В случае отрицательного заряда направление силы при прочих равных условиях изменяется на обратное.
где b — расстояние от заряда до провода. В случае положительного заряда сила направлена к проводу, если направления тока и движения заряда одинаковы, и от провода, если направления тока и движения заряда противоположны (см. рис. 43.2). В случае отрицательного заряда направление силы при прочих равных условиях изменяется на обратное.
Рассмотрим два одноименных' точечных заряда q1 и q2, движущихся вдоль параллельных прямых с одинаковой скоростью v, много меньшей с (рис. 43.3). 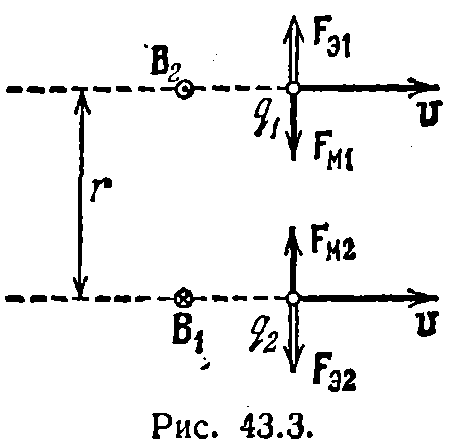 При v< < c электрическое поле практически не отличается от поля неподвижных зарядов. Поэтому величину электрической силы Fa, действующей на заряды, можно считать равной
При v< < c электрическое поле практически не отличается от поля неподвижных зарядов. Поэтому величину электрической силы Fa, действующей на заряды, можно считать равной 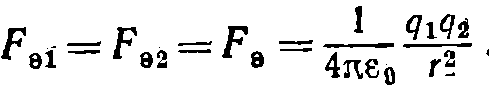 (43/7) Согласно формулам для магнитной силы FM, действующей на заряды, получается выражение
(43/7) Согласно формулам для магнитной силы FM, действующей на заряды, получается выражение 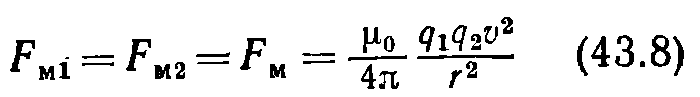 (радиус-вектор г перпендикулярен к v). Найдем отношение магнитной силы к электрической. Из 43.7 и 43.8 следует, что
(радиус-вектор г перпендикулярен к v). Найдем отношение магнитной силы к электрической. Из 43.7 и 43.8 следует, что 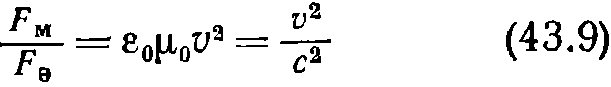 Мы получили соотношение 43.9 в предположении, что v< < c. Однако это соотношение оказывается справедливым при любых V. Направления сил F3 и FM противоположны. Рис. 43.3 выполнен для одноименных и притом положительных зарядов. Для одноименных отрицательных зарядов направления сил останутся теми же, а направления векторов B1 и В2 изменятся на противоположные. Для разноименных зарядов направления электрических и магнитных сил будут противоположны показанным на рисунке. Из 43.9) следует, что магнитная сила слабее кулоновской на множитель, равный квадрату отношения скорости заряда к скорости света. Это объясняется тем, что магнитное взаимодействие между движущимися зарядами является релятивистским эффектом.
Мы получили соотношение 43.9 в предположении, что v< < c. Однако это соотношение оказывается справедливым при любых V. Направления сил F3 и FM противоположны. Рис. 43.3 выполнен для одноименных и притом положительных зарядов. Для одноименных отрицательных зарядов направления сил останутся теми же, а направления векторов B1 и В2 изменятся на противоположные. Для разноименных зарядов направления электрических и магнитных сил будут противоположны показанным на рисунке. Из 43.9) следует, что магнитная сила слабее кулоновской на множитель, равный квадрату отношения скорости заряда к скорости света. Это объясняется тем, что магнитное взаимодействие между движущимися зарядами является релятивистским эффектом.
4) Что такое магнитный момент? Охарактеризовать поведение витка с током в магнитном поле. Известно, что магнитное поле оказывает ориентирующее действие на рамку с током, и рамка поворачивается вокруг своей ося. Происходит это потому, что в магнитном поле на рамку действует момент сил, равный... Здесь B - вектор индукции магнитного поля, I-ток в рамке, S-ее площадь и а-угол между силовыми линиями и перпендикуляром к плоскости рамки. В это выражение входит произведение I*S, которое называют магнитным моментом рамки. Величина магнитного момента полностью характеризует взаимодействие рамки с магнитным полем. Две рамки, у одной из которых большой ток и малая площадь, а у другой - большая площадь и малый ток, будут вести себя в магнитном поле одинаково, если их магнитные моменты равны. Если рамка маленькая, то ее взаимодействие с магнитным полем не зависит от ее формы. Удобно считать магнитный момент вектором. который расположен на линии, перпендикулярной плоскости рамки. Направление вектора определяется " правилом буравчика": буравчик нужно расположить перпендикулярно плоскости рамки и вращать по направлению тока рамки -направление движения буравчика укажет направление вектора магнитного момента. Магнитный момент измеряется в А⋅ м2 или Дж/Тл (СИ). 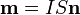 , где
, где 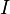 — сила тока в контуре, S — площадь контура, n — единичный вектор нормали к плоскости контура.
— сила тока в контуре, S — площадь контура, n — единичный вектор нормали к плоскости контура.
Магнитное поле витка с током, или контура тока, показано рисунке (кружок с точкой означает, что в этом сечении ток направлен перпендикулярно плоскости рисунка к нам, а кружок с крестом - что ток направлен от нас). Направление линий магнитной индукции вдоль оси витка укажет магнитная стрелка, помещенная в его центре. Две противоположные стороны обтекаемой током поверхности можно сопоставить с двумя полюсами магнитной стрелки: сторону, из которой линии магнитной индукции выходят – с северным полюсом магнитной стрелки, а в которую они входят – с южным.
Направление магнитного поля витка с током можно определить также по правилу правого винта: если поместить острие винта в центре витка и вращать винт в направлении тока, то его поступательное движение укажет направление линий магнитной индукции.Таким образом, существует взаимная связь направлений тока в замкнутом проводнике и его магнитного поля, их «сцепленность». 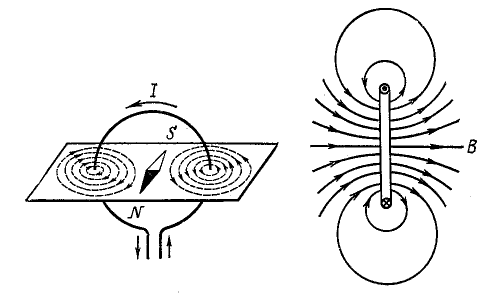
5) Сформулировать теорему Гаусса для магнитных полей и теорему о циркуляции вектора магнитной индукции. Подобно тому, как было введено понятие потока вектора напряженности электрического поля, введем понятие потока вектора магнитной индукции, или магнитного потока. Элементарный магнитный поток 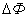 через малую элементарную площадку
через малую элементарную площадку 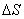 , которую можно считать плоской, и в окрестности которой магнитное поле можно считать однородным, равен произведению вектора индукции на площадь выделенного элемента поверхности и косинус угла между вектором индукции и нормалью к поверхности:
, которую можно считать плоской, и в окрестности которой магнитное поле можно считать однородным, равен произведению вектора индукции на площадь выделенного элемента поверхности и косинус угла между вектором индукции и нормалью к поверхности:
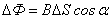 . Поток может быть как положительным, так и отрицательным в зависимости от направления нормали к поверхности. За единицу магнитного потока в системе единиц СИ принят вебер (Вб). 1 Вб – это магнитный поток через поверхность площадью
. Поток может быть как положительным, так и отрицательным в зависимости от направления нормали к поверхности. За единицу магнитного потока в системе единиц СИ принят вебер (Вб). 1 Вб – это магнитный поток через поверхность площадью 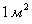 , расположенную в однородном магнитном поле перпендикулярно вектору индукции
, расположенную в однородном магнитном поле перпендикулярно вектору индукции 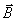 , равному по модулю
, равному по модулю 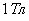 :
:
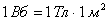 . В случае неоднородного магнитного поля поток через какую-либо поверхность равен алгебраической сумме потоков через участки поверхности, вблизи которых поле можно считать однородным. Магнитный поток, как и поток вектора напряженности электрического поля, можно считать равным числу магнитных силовых линий, пересекающих рассматриваемую поверхность. Магнитное поле является вихревым, то есть его линии магнитной индукции замкнуты. Поэтому замкнутая поверхность, помещенная в магнитное поле, пронизывается линиями магнитной индукции так, что любая линия, входящая в эту поверхность, выходит из нее. Следовательно, полный магнитный поток через произвольную замкнутую поверхность равен нулю. Это утверждение носит название теоремы Гаусса для магнитных полей. Равенство нулю магнитного потока через замкнутую поверхность является следствием того, что в природе нет магнитных зарядов, и магнитные поля образуются только электрическими зарядами. Теорема о циркуляции вектора магнитной индукции Рассмотрим постоянные токи в вакууме.
. В случае неоднородного магнитного поля поток через какую-либо поверхность равен алгебраической сумме потоков через участки поверхности, вблизи которых поле можно считать однородным. Магнитный поток, как и поток вектора напряженности электрического поля, можно считать равным числу магнитных силовых линий, пересекающих рассматриваемую поверхность. Магнитное поле является вихревым, то есть его линии магнитной индукции замкнуты. Поэтому замкнутая поверхность, помещенная в магнитное поле, пронизывается линиями магнитной индукции так, что любая линия, входящая в эту поверхность, выходит из нее. Следовательно, полный магнитный поток через произвольную замкнутую поверхность равен нулю. Это утверждение носит название теоремы Гаусса для магнитных полей. Равенство нулю магнитного потока через замкнутую поверхность является следствием того, что в природе нет магнитных зарядов, и магнитные поля образуются только электрическими зарядами. Теорема о циркуляции вектора магнитной индукции Рассмотрим постоянные токи в вакууме. 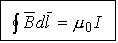 - теорема о циркуляции вектора
- теорема о циркуляции вектора 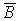 :
:
циркуляция вектора 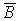 по произвольному контуру равна произведению
по произвольному контуру равна произведению 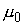 на алгебраическую сумму токов, охватываемых контуром.
на алгебраическую сумму токов, охватываемых контуром.
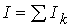 ; ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого
; ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого 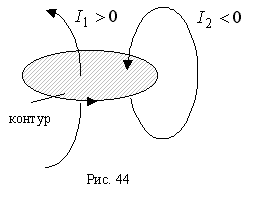 винта (рис. 44).Теорема о циркуляции доказывается посредством закона Био-Савара-Лапласа и подтверждается экспериментально.
винта (рис. 44).Теорема о циркуляции доказывается посредством закона Био-Савара-Лапласа и подтверждается экспериментально.
Для распределенного по объему тока
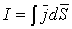
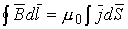
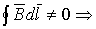 поле не потенциально (в отличие от электростатического поля); магнитное поле - вихревое (соленоидальное или трубчатое) поле, свободное от источников (следует из равенства нулю дивергенции).
поле не потенциально (в отличие от электростатического поля); магнитное поле - вихревое (соленоидальное или трубчатое) поле, свободное от источников (следует из равенства нулю дивергенции).
Соответствующие трубки называются трубками тока; где трубка сжимается, там значение вектора 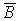 увеличивается (аналогично изменению скорости течения при изменении проходного сечения; поток во всех сечениях одинаков).
увеличивается (аналогично изменению скорости течения при изменении проходного сечения; поток во всех сечениях одинаков).
В пределе при 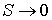
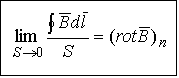 - ротор поля
- ротор поля  (вихрь вектора).
(вихрь вектора).
Здесь  проекция ротора на направление нормали
проекция ротора на направление нормали  к плоскости контура, по которому берется циркуляция.
к плоскости контура, по которому берется циркуляция.
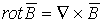 , ротор получается в результате векторного перемножения оператора Гамильтона и вектора магнитной индукции (
, ротор получается в результате векторного перемножения оператора Гамильтона и вектора магнитной индукции ( 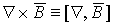 ).
). 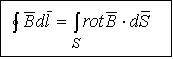 - теорема Стокса.
- теорема Стокса.
Направление ротора 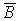 определяется по направлению нормали
определяется по направлению нормали 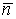 , где
, где 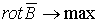 .
.
. 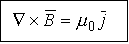 - дифференциальная форма теоремы о циркуляции
- дифференциальная форма теоремы о циркуляции 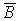 .
.
Для электростатического поля 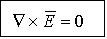
 поле потенциально
поле потенциально  вектор напряженности
вектор напряженности 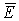 можно представить в виде градиента скалярной функции (потенциала
можно представить в виде градиента скалярной функции (потенциала 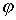 ).
). 
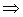 поле соленоидально
поле соленоидально 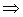 вектор магнитной индукции
вектор магнитной индукции 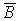 можно представить (как и всякий соленоидальный вектор) как вихрь некоторого другого вектора
можно представить (как и всякий соленоидальный вектор) как вихрь некоторого другого вектора 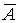 (
( 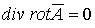 )
) 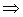
 , где
, где 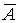 - векторный потенциал.
- векторный потенциал.
Магнитное поле в веществе.
1) Что такое вектор намагниченности? Вектор намагничивания — магнитный момент элементарного объёма, используемый для описания магнитного состояния вещества. По отношению к направлению вектора магнитного поля различают продольную намагниченность и поперечную намагниченность. Поперечная намагниченность достигает значительных величин в анизотропных магнетиках, и близка к нулю в изотропных магнетиках. Поэтому, в последних возможно выразить вектор намагничивания через напряжённость магнитного поля и коэффициент 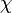 названный магнитной восприимчивостью:
названный магнитной восприимчивостью: 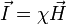
Популярное:
- I. ТИТУЛ «ИНТЕРНАЦИОНАЛЬНЫЙ ЧЕМПИОН ПО КРАСОТЕ» (C.I.B.) ДЛЯ ПОРОД С ОБЯЗАТЕЛЬНЫМИ И НЕОБЯЗАТЕЛЬНЫМИ РАБОЧИМИ ИСПЫТАНИЯМИ СОГЛАСНО НОМЕНКЛАТУРЕ FCI.
- Автор затрагивает вопрос (о чем?)
- Берите «на карандаш» все замеченные ошибки и пытайтесь ответить на вопрос, поставленный «акулой пера»: «Интересно, почему?»
- БОЛЬШАЯ ПОТАСОВКА МЕЖДУ ПИНОККИО И ЕГО ТОВАРИЩАМИ, ПРИЧЁМ ОДИН ИЗ НИХ РАНЕН, И ПИНОККИО АРЕСТОВЫВАЮТ ПОЛИЦЕЙСКИЕ
- БОЛЬШАЯ ПОТАСОВКА МЕЖДУ ПИНОККИО И ЕГО ТОВАРИЩАМИ, ПРИЧЕМ ОДИН ИЗ НИХ РАНЕН, И ПИНОККИО АРЕСТОВЫВАЮТ ПОЛИЦЕЙСКИЕ
- Больше дьяволов, чем может вместить ад
- Больше дьяволов, чем может вместить необъятный ад
- Больше чем половинчатое решение: разрушайте, разрушайте
- Будущее еще загадочней, чем ты думаешь
- Бывало ли вам когда-нибудь грустно, и вы бы не знали чем себя занять?
- Бытие как исходная философская категория. Трактовка категории бытия в истории философии.
- В основной части выступления можно использовать прием «эллипса» – недоговаривания последнего слова фразы. Слушатели сами договаривают это слово, чем вовлекаются в процесс активного восприятия.

