ИЗУЧЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

Лабораторная работа № 4

ИЗУЧЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

Цель работы: Изучение динамики вращательного движения, измерение момента инерции маятника Обербека.

Теоретическая часть

Вращательным движением называется такое движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения. Вращательное движение тела описывают с помощью углового перемещения - вектора, численно равного углу поворота тела и направленного вдоль оси вращения так, что если смотреть с его конца, то вращение тела видится происходящим против часовой стрелки. Быстрота изменения вектора углового перемещения характеризуется угловой скоростью :

. (4.1)

В свою очередь, быстрота изменения вектора угловой скорости характеризуется угловым ускорением :

(4.2)

Линейная скорость , тангенциальное и нормальное ускорения любой точки вращающегося твердого тела связаны с характеристиками вращательного движения следующими соотношениями:

= R, = R , = R, (4.3)

где R – расстояние от рассматриваемой точки тела до оси вращения.

Мерой инертности тела при вращательном движении служит момент инерции J. Это скалярная величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний r_i до оси вращения:

J = . (4.4)

В случае непрерывного распределения масс эта сумма сводится к интегралу:

J = , (4.5)

где V – объем тела.

Для описания вращательного движения твердого тела вводят понятие момента силы относительно неподвижной точки. Это векторная величина, равная векторному произведению радиус-вектора , проведенного из начала координат в точку приложения силы , и силы :

. (4.6)

Модуль момента силы

М = F r sin = F l, (4.7)

где l = r sin - плечо силы, - угол между векторами и .

Основное уравнение динамики вращательного движения записывается следующим образом:

. (4.8)

Угловое ускорение, приобретаемое твердым телом, прямо пропорционально результирующему моменту всех действующих на тело внешних сил и обратно пропорционально моменту инерции тела.

Постановка экспериментальной задачи

В данной работе осуществляется экспериментальная проверка основного уравнения динамики вращательного движения (4.8) с помощью маятника Обербека. Маятник представляет собой маховик, которому придана крестообразная форма (рис. 4.1).

Рис. 4.1.

По четырем взаимно-перпендикулярным стержням могут перемещаться грузы массой m₀. На общей оси находится шкив, на который наматывается нить с привязанным к ней грузом массой m. Под действием падающего груза нить разматывается и приводит маховик в равноускоренное вращательное движение. При этом угловое ускорение крестовины определяется соотношением:

, (4.9)

где а – ускорение падающего груза, r = d/2 – радиус шкива.

В свою очередь, пользуясь известным выражением для равноускоренного движения груза:

, (4.10)

( h – высота падения груза, t – время падения груза)

находим:

, (4.11)

или, используя (4.9):

. (4.12)

Момент силы, приложенной к крестовине, находим по формуле:

, (4.13)

где F – сила, действующая на шкив.

Но , и =1. Тогда формула (4.13) имеет вид:

Силу F можно найти из уравнения движения груза:

, (4.14)

где m – масса падающего груза, а , - сила натяжения нити. Тогда для момента силы получим следующее выражение:

. (4.15)

Используя формулу (4.8) получим:

. (4.16)

Получив экспериментальные значения h и t, по формуле (4.16) определяем значение момента инерции крестовины. Теоретическое значение момента инерции крестовины можно рассчитать следующим образом:

, (4.17)

где m₀ = 0, 114 кг– масса подвижного груза крестовины; R - расстояние от центра масс подвижного груза до оси вращения, м;

r₀= 0, 015 м – радиус груза;

l = 0, 02 м – длина образующей груза.

Момент инерции системы без грузов J₀ определить по формуле:

, (4.18)

где l₁= 0, 15 м – длина одного из стержней крестовины;

m₁= 0, 023 кг – масса стержня.

Лабораторная работа № 8

МАТЕМАТИЧЕСКИЙ И ФИЗИЧЕСКИЙ МАЯТНИКИ

Цель работы: Изучение колебаний математического и физического маятников; определение ускорения свободного падения.

Теоретическая часть

Рис. 8.1

Рис. 8.1.

Простейшим примером гармонических колебаний является движение так называемого математического маятника. Математическим маятником называется маятник, состоящий из материальной точки массой m, подвешенной на невесомой нерастяжимой нити длиной и колеблющейся около точки О. В этом случае центр тяжести системы можно считать совпадающим с центром тяжести груза. Напишем уравнение движения для математического маятника, находящегося в поле тяготения и отклоненного от состояния равновесия на угол a. Система, выведенная из состояния устойчивого равновесия и предоставленная самой себе, совершает колебания, называемые свободными. На маятник в отклоненном состоянии действует сила (рис. 8.1): Р_t=mg sina. Она направлена по касательной к траектории груза в сторону положения равновесия. Уравнение движения груза будет иметь вид:

, (8.1)

В этой записи уравнения учтено, что возвращающая сила всегда направлена в сторону, противоположную направлению возрастания смещения х. При малых отклонениях маятника от положения равновесия (угол a не превышает 5-6 град.) можно считать, что , т.е. смещение по дуге можно считать приближенно равным смещению вдоль горизонтальной хорды. Уравнение (8.1) обычно записывается в виде:

, (8.2)

где – циклическая частота гармонических колебаний.

Решением этого дифференциального уравнения является выражение:

Период колебаний определяется формулой:

. (8.3)

Из этой формулы видно, что период колебаний математического маятника зависит только от ускорения силы тяжести в данном месте Земли и от длины маятника, и не зависит от амплитуды колебаний и от массы груза. Измеряя Т и используя формулу (8.3), можно вычислить ускорение свободного падения в данном месте земной поверхности. Этим методом впервые было измерено значение g на разных широтах земного шара, в результате чего была установлена зависимость g от широты j. Если измерить для нескольких значений соответствующие периоды колебаний ( , где t-время n полных колебаний), затем построить график зависимости Т² от , то согласно формуле (8.3) эта зависимость может быть представлена в виде прямой типа: y = ax. Тангенс угла наклона этой прямой численно равен:

Отсюда можно найти ускорение свободного падения g:

Рис.8.2.

Другой колебательной системой, с помощью которой можно определить ускорение свободного падения, является физический маятник. Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 8.2).

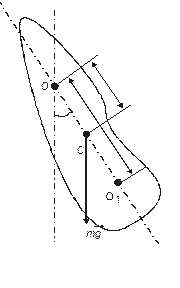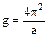Из-за наличия трения часть механической энергии маятника рассеивается в виде тепла, поэтому колебания всегда затухают. Так как маятник совершает вращательные колебания, то они описываются основным уравнением динамики вращательного движения относительно неподвижной оси:

, (8.4)

где J=J₀+m – момент инерции маятника относительно оси, проходящей через точку О; J₀– его момент относительно центра масс; – угловое ускорение; М_w – проекция результирующего момента всех сил, действующих на тело, на ось вращения. Он складывается из вращательного момента, создаваемого силой тяжести:

и тормозящего момента, создаваемого силами трения:

где k – коэффициент трения, – угловая скорость. Знак «–» в формуле для вращательного момента отражает тот факт, что возвращающая сила всегда направлена к положению равновесия, а в формуле для тормозящего момента то, что сила сопротивления направлена всегда против направления движения.

При малых углах отклонения , тогда , и уравнение (8.4) можно представить в виде:

. (8.5)

Введя обозначения: , где b – коэффициент затухания; , где w₀ – собственная частота маятника, получаем универсальный вид дифференциального уравнения свободных затухающих колебаний:

, (8.6)

его решением является функция:

, (8.7)

где – частота свободных затухающих колебаний, - начальная фаза.

Период свободных затухающих колебаний можно найти по формуле:

. (8.8)

Если считать, что затухание колебаний мало (см. конструкцию прибора), то им можно пренебречь в выражении (8.8). Учитывая, что

получаем для периода колебаний физического маятника следующую формулу:

. (8.9)

где - приведенная длина физического маятника.

Тогда значение ускорения свободного падения можно найти по формуле:

. (8.10)

Таблица 8.1

	, м	t, с	, с²
1. … 10.

Снимите физический (оборотный) маятник с верхнего кронштейна.
Установить нижний кронштейн с фотодатчиком в крайнее нижнее положение шкалы так, чтобы плоскость кронштейна, окрашенная в синий цвет, совпала с одной из рисок шкалы.
Установить верхний кронштейн таким образом, чтобы шарик математического маятника оказался в рабочей зоне фотодатчика. При помощи устройства 10 добиться такого положения шарика, при котором его центральная риска будет совпадать по высоте с риской на фотодатчике.
По шкале вертикальной стойки определите длину математического маятника . Результаты занесите в таблицу.
Нажмите кнопку «СЕТЬ» блока.
Приведите математический маятник в колебательной движение, отклонив металлический шарик на угол примерно 5-6 градусов, одновременно нажав кнопку «ПУСК» на блоке.
По показанию таймера определите значение времени 20 колебаний маятника, нажав кнопку «СТОП». Занесите значение t в таблицу.
Определите значение периода колебаний маятника по формуле: T = t/n (n – число колебаний).
Определите значения Т² и запишите в таблицу.
Повторите п.п.5-10 для 10 разных значений .
Постройте график зависимости T² от и по нему определите угловой коэффициент , и рассчитайте значение g.
Определите погрешность полученного значения g.

Задание 2: Определить значение ускорения свободного падения g с помощью физического (оборотного) маятника.

Зарисуйте таблицу 8.2.

	n = 10
	t₁, с	T₁, с	t₂, с	T₂	T₁/T₂

…

	=, м

Укрепите призматическую опору 12 на расстоянии около 120 мм от конца стержня 11 физического (оборотного) маятника и два груза 13 в положениях, обозначенных на рис. 8.3.
Подвесьте оборотный маятник на одной из призматических опор. Поверните верхний кронштейн на 180 градусов так, чтобы стержень маятника находился в рабочей зоне фотодатчика.
Отклоните маятник на угол примерно 5-6 градусов, нажмите кнопку «ПУСК» на блоке и без толчка отпустите маятник. По показанию таймера определите значение времени 10 колебаний маятника, нажав кнопку «СТОП». Определите значение периода колебаний маятника по формуле: T₁ = t₁/n.
Поверните маятник и подвесьте его на другой призматической опоре.
Отклоните маятник на угол примерно 5-6 градусов, нажмите кнопку «ПУСК» на блоке и без толчка отпустите маятник. По показанию таймера определите значение времени 10 колебаний маятника, нажав кнопку «СТОП». Определите значение периода колебаний маятника по формуле: T₂ = t₂/n.
Перемещением призматических опор и грузов на стержне добейтесь примерного совпадения периодов колебания маятника при его качании на обеих призматических опорах с точностью не более 0, 5% (T₁/ T₂=0, 995).
Определите расстояние между опорными гранями двух призматических опор при помощи линейки и вычислите ускорение свободного падения g по формуле (8.10).
Определите погрешность полученного значения .
Сравните найденные значения g с табличным значением и сделайте вывод.

Задание 3: Определить положение центра масс физического маятника.

Установите грузы 13 в произвольном положении на стержне 11 физического (оборотного) маятника (рис. 8.3).
Определите периоды колебаний оборотного маятника Т₁ и Т₂ в соответствии с п.п. 3-5 задания 2 (сначала на одной призматической опоре, затем перевернув его).
Определите расстояние от центра масс до точки подвеса по формуле:

где L – расстояние между призматическими опорами, м (измерьте при помощи линейки).

Контрольные вопросы

1. Что называется математическим и физическим маятниками?

2. При каких условиях колебания этих маятников являются гармоническими?

3. Получите дифференциальное уравнение гармонических колебаний математического маятника.

4. Получите дифференциальные уравнения затухающих и незатухающих колебаний физического маятника.

5. Напишите решение дифференциального уравнения затухающих колебаний и представьте его графически.

6. Что такое приведенная длина физического маятника?

7. Как определяется графически и D для математического и физического маятников?

Лабораторная работа № 9

Теоретическая часть

Второй закон Ньютона утверждает, что скорость изменения импульса тела равна действующей на частицу силе :

Это соотношение называется уравнением движения частицы (под частицей подразумевается материальная точка). Подставив в это соотношение выражение для импульса, получим, что:

Приняв во внимание, что m=const, а , придем к соотношению:

Мы получили вторую формулировку второго закона Ньютона: произведение массы частицы на ее ускорение равно силе, действующей на частицу. Это уравнение справедливо и для протяженных тел в том случае, когда они движутся поступательно. Если при этом ускорение остается постоянным, то такое движение называется равноускоренным. В этом случае зависимость пути от времени выражается формулой:

а скорость растет линейно со временем:

Описание экспериментальной установки

Общий вид установки приведен на рис.9.1.

На вертикальной стойке 2 основания 1 расположены верхний кронштейн 3, кронштейн 4 для установки фотодатчика, фотодатчик 5. Основание 1 снабжено тремя регулируемыми опорами 6 и винтом-барашком 7 для фиксации вертикальной стойки 2.

Вертикальная стойка 2 выполнена из металлической трубы, на которую нанесена миллиметровая шкала, и имеет визир 14.

На верхнем кронштейне 3 размещается узел подшипников 8 с малоинерционным шкивом 9, через который перекинута капроновая нить 10 с двумя основными грузами 11 и набором разновесов 12, электромагнитный тормоз 13, предназначенный для фиксации исходного положения грузов. Верхний кронштейн 3 имеет винт-барашек для крепления на вертикальной стойке 2.

Кронштейн 4 имеет винт-барашек для крепления на вертикальной стойке 2 и элементы фиксации фотодатчика.

Принцип работы устройства

Принцип работы установки состоит в том, что когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если на один из грузов положить перегрузок массой m система выходит из равновесия и начинает двигаться равноускоренно. В комплект добавочных грузов входит несколько перегрузков, что позволяет исследовать движение с разными ускорениями. На каждый груз действуют две силы – сила тяжести и натяжение нити, под действием которых грузы движутся. Предполагая, что нити и блок невесомы, нить нерастяжима, а сила трения мала, получим, что ускорение обоих грузов будут одинаковы по величине и противоположны по направлению, а натяжение нити одинаковы справа и слева. На основании второго закона Ньютона можно записать для груза с перегрузком:

(M+m)a=(M+m)g – T, (9.1)

где М – масса груза, m – масса перегрузка, а – ускорение грузов, g – ускорение свободного падения, Т – сила натяжения нити. Для груза без перегрузка:

-Ma = Mg - T. (9.2)

Исходя из этих уравнений, получим теоретическое значение ускорения:

. (9.3)

Ускорение при таком движении можно также найти из известного соотношения для равноускоренного движения:

, (9.4)

где S – путь, пройденный грузами; t – время движения грузов. Зная пройденный путь и время движения, определяем экспериментальное значение ускорения:

. (9.5)

Таблица 9.1

М=0.05 кг; m= кг
№	1	2	3	4	5
S, м
t, c




, с
a_э, м/с²

Задание 2: Проверка 2-го закона Ньютона.

При проверке этого закона необходимо, чтобы масса движущейся системы оставалась постоянной, а величина действующей силы изменялась. Это можно осуществить, перекладывая перегрузки m₁ и m₂ (m₁> m₂) с одного груза на другой. Если оба перегрузка находятся на правом грузе, то уравнения движения грузов по II закону Ньютона:

где Т – сила натяжения нити.

Решая совместно эти два уравнения, находим:

. (9.7)

Если меньший перегрузок m₂ переложить на левый груз, тогда уравнения движения грузов запишутся в следующем виде:

Исключая из этих уравнений F_н, получим:

. (9.8)

Учитывая, что при S₁=S₂, получим:

. (9.9)

Для проверки этого соотношения:

1. Положить на правый груз перегрузки m₁и m₂(m₁> m₂). Записать по показаниям секундомера значение времени движения грузов.

2. Повторить эксперимент пять раз.

3. Переложить перегрузок m₂ на левый груз и повторить те же измерения, что и в первом пункте.

4. Данные занесите в таблицу 9.2.

5. Проверьте формулу (9.9) по условию эксперимента ( с учетом погрешности) и сделайте вывод о справедливости II закона Ньютона.

Таблица 9.2

	m₁ + m₂	m₁ - m₂
№	t₁, c	, c²	а₁ м/c²	t₂, c	, c²	а₂, м/c²
1.
2.
3.
4.
5.
ср.зн.

Контрольные вопросы

1. Какое движение тела называется поступательным?

2. Опишите виды поступательного движения.

3. Определите кинетические параметры поступательного движения (a, v, S) и объясните их физический смысл.

4. Как определить скорость и ускорение поступательного движения, если задан закон движения?

5. Сформулируйте законы Ньютона, запишите их в векторной и в скалярной формах.

6. Объясните методику проверки второго закона Ньютона.

Лабораторная работа № 4

ИЗУЧЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА

Цель работы: Изучение динамики вращательного движения, измерение момента инерции маятника Обербека.

Теоретическая часть

. (4.1)

В свою очередь, быстрота изменения вектора угловой скорости характеризуется угловым ускорением :

(4.2)

= R, = R , = R, (4.3)

где R – расстояние от рассматриваемой точки тела до оси вращения.

J = . (4.4)

В случае непрерывного распределения масс эта сумма сводится к интегралу:

J = , (4.5)

где V – объем тела.

. (4.6)

Модуль момента силы

М = F r sin = F l, (4.7)

где l = r sin - плечо силы, - угол между векторами и .

Основное уравнение динамики вращательного движения записывается следующим образом:

. (4.8)

12	Поделиться: