Методика эксперимента и обработка результатов измерения

Задание 1. Определить момент инерции крестовины.

1. Зарисовать таблицу 4.1.

Таблица 4.1

r₁= 0, 02 м; h = м; g = 9, 8 м/ с²
m₁= кг.
t, c						tcp, c
m₂= кг.
t, c						tcp, c
m₃= кг.
t, c						tcp, с

2. Установить подвижные грузы по осям крестовины на расстоянии 100 мм от оси вращения.

3. Закрепить нить на малом радиусе r₁двухступенчатого шкива. Установить на платформу основного груза один разновес.

4. Установить кронштейн с фотодатчиком в нижней части шкалы вертикальной стойки так, чтобы плоскость кронштейна, окрашенная в красный цвет, совпала с одной из рисок шкалы, а наборный груз при движении вниз проходил по центру рабочего окна фотодатчика. За нижнее положение груза берется отметка шкалы, соответствующая риске на корпусе фотодатчика и являющаяся как бы продолжением оптической оси фотодатчика, которую пересекает движущийся груз.

5. Вращая маятник, установить груз в крайнем верхнем положении таким образом, чтобы нижняя плоскость груза (визир вертикальной стойки соприкасается с нижней плоскостью груза) совпала с одной из рисок шкалы вертикальной стойки.

6. Зафиксировать груз в этом положении. Для этого нажать кнопку «СЕТЬ» секундомера, при этом должен сработать фрикцион электромагнитного тормоза.

ВНИМАНИЕ. Для предотвращения перегревания катушки электромагнитного тормоза – время непрерывной работы электромагнитного тормоза - не более 15 секунд, перерыв – 5 секунд.

7. Нажать кнопку «СТАРТ» секундомера. Происходит растормаживание электромагнитного тормоза, груз начинает опускаться и таймер блока начинает отсчет времени. При пересечении грузом оптической оси фотодатчика отсчет времени прекратится. Записать показание таймера, т.е. время движения груза t.

8. При помощи визира по шкале вертикальной стойки определить пройденный грузом путь h, как расстояние от нижней плоскости груза в верхнем положении груза до оптической оси фотодатчика.

9. Повторить измерения по п.п. 5-8 пять раз и определить среднее значение времени. Результаты занести в таблицу 4.1.

10. Определить момент инерции крестовины по формуле (4.16).

11. Аналогичные измерения произвести, установив на платформу основного груза два, а затем три разновеса.

12. Сравнить полученные значения момента инерции крестовины с учетом погрешности. Сделать вывод.

13. Определить теоретическое значение момента инерции крестовины по формуле (4.17) и сравнить с экспериментальными значениями.

14. Определить относительную погрешность полученных значений по формуле:

15. Повторить выполнение п.п. 5-14, закрепив нить на большом радиусе r₂ двухступенчатого шкива. Результаты занести в таблицу 4.2.

Таблица 4.2

r₂= 0, 035 м; h = м; g = 9, 8 м/ с²
m₁= кг.
t, c						tcp, c
m₂= кг.
t, c						tcp, c
m₃= кг.
t, c						tcp, с

Задание 2. Определение зависимости момента инерции J от расстояния грузов до оси вращения крестовины R.

1. Передвинуть все грузы на один сантиметр к оси вращения.

2. Сделать измерения по пунктам 3-8 задания 1 (используя малый радиус шкива и один разновес на основном грузе).

3. Повторить п.п. 1-2 пять раз. Результаты занести в таблицу 4.3.

4. Определить момент инерции крестовины по формуле (4.16). Проанализировать полученные значения момента инерции крестовины. Сделать вывод.

5. Построить график зависимости J = f(R).

Таблица 4.3

r₁= 0, 02 м; h= м;
R₁=	R₂=	R₃=	R₄=	R₅=
t₁	t₂	t₃	t₄	t₅





t_1ср=	t_2ср=	t_3ср=	t_4ср=	t_5ср=

Контрольные вопросы

1. Сформулируйте основное уравнение динамики вращательного движения и дайте определение всем величинам, входящим в уравнение.

2. Выведите рабочую формулу данной работы (4.16).

3. Укажите основные источники погрешностей измерений. Выведите формулу для расчета погрешности J.

4. Какую роль играет момент инерции при вращательном движении? Объясните физический смысл момента инерции.

5. От чего зависит момент инерции маятника Обербека (формула (4.17))?

6.Выведите формулы для момента инерции цилиндра и стержня?

Лабораторная работа № 8

МАТЕМАТИЧЕСКИЙ И ФИЗИЧЕСКИЙ МАЯТНИКИ

Цель работы: Изучение колебаний математического и физического маятников; определение ускорения свободного падения.

Теоретическая часть

Рис. 8.1

Рис. 8.1.

Простейшим примером гармонических колебаний является движение так называемого математического маятника. Математическим маятником называется маятник, состоящий из материальной точки массой m, подвешенной на невесомой нерастяжимой нити длиной и колеблющейся около точки О. В этом случае центр тяжести системы можно считать совпадающим с центром тяжести груза. Напишем уравнение движения для математического маятника, находящегося в поле тяготения и отклоненного от состояния равновесия на угол a. Система, выведенная из состояния устойчивого равновесия и предоставленная самой себе, совершает колебания, называемые свободными. На маятник в отклоненном состоянии действует сила (рис. 8.1): Р_t=mg sina. Она направлена по касательной к траектории груза в сторону положения равновесия. Уравнение движения груза будет иметь вид:

, (8.1)

В этой записи уравнения учтено, что возвращающая сила всегда направлена в сторону, противоположную направлению возрастания смещения х. При малых отклонениях маятника от положения равновесия (угол a не превышает 5-6 град.) можно считать, что , т.е. смещение по дуге можно считать приближенно равным смещению вдоль горизонтальной хорды. Уравнение (8.1) обычно записывается в виде:

, (8.2)

где – циклическая частота гармонических колебаний.

Решением этого дифференциального уравнения является выражение:

Период колебаний определяется формулой:

. (8.3)

Из этой формулы видно, что период колебаний математического маятника зависит только от ускорения силы тяжести в данном месте Земли и от длины маятника, и не зависит от амплитуды колебаний и от массы груза. Измеряя Т и используя формулу (8.3), можно вычислить ускорение свободного падения в данном месте земной поверхности. Этим методом впервые было измерено значение g на разных широтах земного шара, в результате чего была установлена зависимость g от широты j. Если измерить для нескольких значений соответствующие периоды колебаний ( , где t-время n полных колебаний), затем построить график зависимости Т² от , то согласно формуле (8.3) эта зависимость может быть представлена в виде прямой типа: y = ax. Тангенс угла наклона этой прямой численно равен:

Отсюда можно найти ускорение свободного падения g:

Рис.8.2.

Другой колебательной системой, с помощью которой можно определить ускорение свободного падения, является физический маятник. Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 8.2).

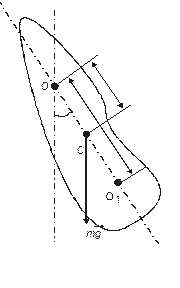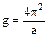Из-за наличия трения часть механической энергии маятника рассеивается в виде тепла, поэтому колебания всегда затухают. Так как маятник совершает вращательные колебания, то они описываются основным уравнением динамики вращательного движения относительно неподвижной оси:

, (8.4)

где J=J₀+m – момент инерции маятника относительно оси, проходящей через точку О; J₀– его момент относительно центра масс; – угловое ускорение; М_w – проекция результирующего момента всех сил, действующих на тело, на ось вращения. Он складывается из вращательного момента, создаваемого силой тяжести:

и тормозящего момента, создаваемого силами трения:

где k – коэффициент трения, – угловая скорость. Знак «–» в формуле для вращательного момента отражает тот факт, что возвращающая сила всегда направлена к положению равновесия, а в формуле для тормозящего момента то, что сила сопротивления направлена всегда против направления движения.

При малых углах отклонения , тогда , и уравнение (8.4) можно представить в виде:

. (8.5)

Введя обозначения: , где b – коэффициент затухания; , где w₀ – собственная частота маятника, получаем универсальный вид дифференциального уравнения свободных затухающих колебаний: