Построение экспериментального графика
1. Запустите программу Excel (Пуск ► Программы ► Microsoft Excel) и откройте рабочую книгу, созданную ранее.
2. Выберите щелчком на ярлычке неиспользуемый рабочий лист или создайте новый (Вставка ► Лист). Дважды щелкните на ярлычке листа и переименовать его как Обработка эксперимента.
3. В столбец A, начиная с ячейки A1, введите произвольный набор значений независимой переменной.
4. В столбец B, начиная с ячейки B1, введите произвольный набор значений функции.
5. Методом протягивания выделите все заполненные ячейки столбцов A и B.
6. Щелкните на значке Мастер диаграмм на стандартной панели инструментов.
7. В списке Тип выберите пункт Точечная (для отображения графика, заданного парами значений). В палитре Вид выберите средний пункт в первом столбце (маркеры, соединенные гладкими кривыми). Щелкните на кнопке Далее.
8. Так как диапазон ячеек был выделен заранее, мастер диаграмм автоматически определяет расположение рядов данных. Убедитесь, что данные на диаграмме выбраны правильно. На вкладке Ряд в поле Имя укажите: Результаты измерений. Щелкните на кнопке Далее.
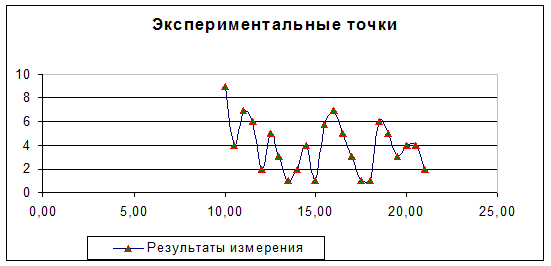
9. Выберите вкладку Заголовки. Убедитесь, что заданное название ряда данных автоматически использовано как заголовок диаграммы. Замените его, введя в поле Название диаграммы заголовок Экспериментальные точки. Щелкните на кнопке Далее.
10. Установите переключатель Отдельном. По желанию, задайте произвольно добавляемого рабочего листа. Щелкните на кнопке Готово.
11. Убедитесь, что диаграмма построена и внедрена на новый рабочий лист, посмотрите ее и щелкните на построенной кривой, чтобы выделить ряд данных.
12. Дайте команду Формат ► Выделенный ряд. Откройте вкладку Вид.
13. На панели Линия откройте палитру Цвет и выберите красный цвет. В списке Тип линии выберите пунктир.
14. На панели Маркер выберите в списке Тип маркера треугольный маркер. В палитрах Цвет и Фон выберите зеленый цвет.
15. Щелкните на кнопке Ok, снимите выделение с ряда данных и посмотрите, как изменится вид графика.
16. Сохраните рабочую книгу.
Таблица 5 Пример построения экспериментального графика (график построен на том же листе).
|
| A
| B
| |
| 21, 00
|
| |
| 20, 50
|
| |
| 20, 00
|
| |
| 19, 50
|
| |
| 19, 00
|
| |
| 18, 50
|
| |
| 18, 00
|
| |
| 17, 50
|
| |
| 17, 00
|
| |
| 16, 50
|
| |
| 16, 00
|
| |
| 15, 50
| 5, 8
| |
| 15, 00
|
| |
| 14, 50
|
| |
| 14, 00
|
| |
| 13, 50
|
| |
| 13, 00
|
| |
| 12, 50
|
| |
| 12, 00
|
| |
| 11, 50
|
| |
| 11, 00
|
| |
| 10, 50
|
| |
| 10, 00
|
| 
Пример построения графика по заданной функции.
Таблица 6 Данные для графика.
|
| A
| B
| |
| x
| f(x)
| |
|
|
| |
|
| 0.173648
| |
|
| 0.34202
| |
|
| 0.5
| |
|
| 0.642788
| |
|
| 0.766044
| |
|
| 0.866025
| |
|
| 0.939693
| |
|
| 0.984808
| |
|
|
| |
|
| 0.984808
| |
|
| 0.939693
| |
|
| 0.866025
| |
|
| 0.766044
| |
|
| 0.642788
| |
|
| 0.5
| |
|
| 0.34202
| |
|
| 0.173648
| |
|
| 1.23E-16
| |
|
| -0.17365
| |
|
| -0.34202
| |
|
| -0.5
| |
|
| -0.64279
| |
|
| -0.76604
| |
|
| -0.86603
| |
|
| -0.93969
| |
|
| -0.98481
| |
|
| -1
| |
|
| -0.98481
| |
|
| -0.93969
| |
|
| -0.86603
| |
|
| -0.76604
| |
|
| -0.64279
| |
|
| -0.5
| |
|
| -0.34202
| |
|
| -0.17365
| |
|
| -2.5E-16
| Построить график функции 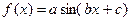 , где a, b, c – произвольные значения, первоначально равные 1, 1, 0. Аргумент функции x изменяется то 0º до 360º с интервалом 10º. , где a, b, c – произвольные значения, первоначально равные 1, 1, 0. Аргумент функции x изменяется то 0º до 360º с интервалом 10º.
1. В столбец A заносим значения аргумента (Таблица 6).
2. В столбце C задаем значения констант ( 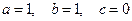 ). ).
3. В столбце B вычисляем функцию относительно x.
4. Строим график по данным функции на том же листе.
5. По оси x записываем значения аргумента.
График построен.
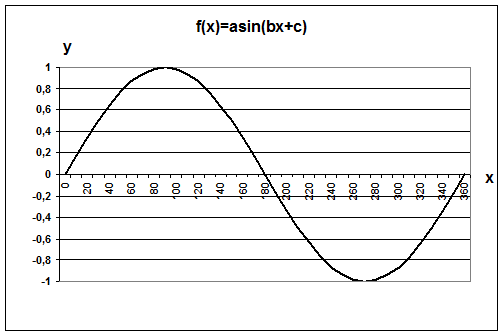
Рис. 9 График функции.
Самостоятельная работа [2]
| 1.
| 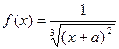 , где x1=-2.25, шаг 0, 2 , где x1=-2.25, шаг 0, 2
| 18.
| 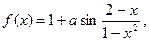 где x1=-2p, шаг p/6. где x1=-2p, шаг p/6.
| | 2.
| 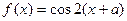 , где x1=-3p, шаг p/6. , где x1=-3p, шаг p/6.
| 19.
| 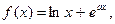 где x1=0, 0001, шаг 1.34. где x1=0, 0001, шаг 1.34.
| | 3.
| 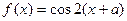 , где x1=0.015, шаг 0, 015. , где x1=0.015, шаг 0, 015.
| 20.
| 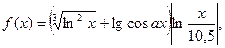 где x1=-2p, шаг p/6. где x1=-2p, шаг p/6.
| | 4.
| 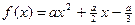 , где x1=-3, шаг 0, 23. , где x1=-3, шаг 0, 23.
| 21.
| 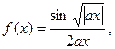 где x1=-2p, шаг p/8. где x1=-2p, шаг p/8.
| | 5.
|  где x1=-2, шаг, 0, 015. где x1=-2, шаг, 0, 015.
| 22.
|  где x1=-2p, шаг, p/8. где x1=-2p, шаг, p/8.
| | 6.
| 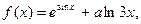 где x1=3, шаг, 0, 23. где x1=3, шаг, 0, 23.
| 23.
| 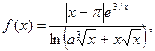 где x1=0, 005, шаг, 0, 0015. где x1=0, 005, шаг, 0, 0015.
| | 7.
| 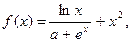 где x1=0, 0001, шаг 0, 5. где x1=0, 0001, шаг 0, 5.
| 24.
| 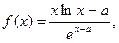 где x1=0, 0001, шаг, 0, 15. где x1=0, 0001, шаг, 0, 15.
| | 8.
|  где x1=-p, шаг –, p/3. где x1=-p, шаг –, p/3.
| 25.
| 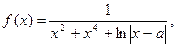 где x1=0, 008, шаг, 0, 05. где x1=0, 008, шаг, 0, 05.
| | 9.
| 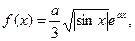 где x1=-p, шаг –, p/6. где x1=-p, шаг –, p/6.
| 26.
| 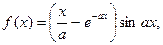 где x1=-p, шаг –, p/6. где x1=-p, шаг –, p/6.
| | 10.
| 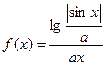 , где x1=-p, шаг, p/8. , где x1=-p, шаг, p/8.
| 27.
| 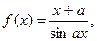 где x1=-p, шаг –, p/4. где x1=-p, шаг –, p/4.
| | 11.
|  где x1=-2, шаг, 0, 15. где x1=-2, шаг, 0, 15.
| 28.
| 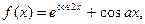 где x1=-1, шаг, 0, 15. где x1=-1, шаг, 0, 15.
| | 12.
| 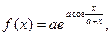 где x1=2, шаг, 0, 15. где x1=2, шаг, 0, 15.
| 29.
| 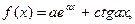 где x1=-p, шаг, p/3. где x1=-p, шаг, p/3.
| | 13.
| 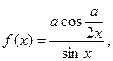 где x1=-p, шаг, p/3. где x1=-p, шаг, p/3.
| 30.
| 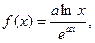 где x1=0, 0001, шаг, 0, 5. где x1=0, 0001, шаг, 0, 5.
| | 14.
| 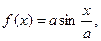 где x1=-2, шаг, 0, 15. где x1=-2, шаг, 0, 15.
| 31.
| 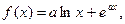 где x1=0, 0001, шаг, 0, 5. где x1=0, 0001, шаг, 0, 5.
| | 15.
| 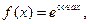 где x1=-2, шаг, 0, 15. где x1=-2, шаг, 0, 15.
| 32.
| 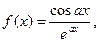 где x1=-1, шаг, 0, 15. где x1=-1, шаг, 0, 15.
| | 16.
| 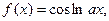 где x1=0, 0001, шаг, 0, 3. где x1=0, 0001, шаг, 0, 3.
| 33.
| 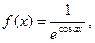 где x1=-2p, шаг, p/8. где x1=-2p, шаг, p/8.
| | 17.
|  , где x1=0, 0001, шаг, 0, 15. , где x1=0, 0001, шаг, 0, 15.
| 34.
| 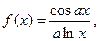 где x1=p, шаг, p/6. где x1=p, шаг, p/6.
|
Построение графика функции с двумя переменными.
Построим график функции  . .
1. В столбец B (начиная с ячейки B3)– заносим значения переменной y.
2. В строку 2 (начиная с ячейки C2) – заносим значения переменной x.
3. В ячейку C3 – введем формулу, таким образом, чтобы значение переменной y бралось из столбца B, а значение переменной x – из строки 2.
4. Скопируем формулу по строке 2, по всем значениям.
5. Скопируем строку 2 по высоте столбца B со значениями y.
6. Выделим диапазон полученных значений функции и построим поверхность, используя мастер диаграмм (Рис. 10).
7. =sin(C$2)*cos($B3)
Таблица 7 Построение графика функции с двумя переменными.
|
| A
| B
| C
| D
| E
| F
| G
| H
| I
| |
|
|
| x
|
|
|
|
|
|
| |
|
|
| -3.00
| -2.85
| -2.70
| -2.55
| -2.40
| -2.25
| -2.10
| |
| y
| 2.00
| 0.059
| 0.120
| 0.178
| 0.232
| 0.281
| 0.324
| 0.359
| |
|
| 2.15
| 0.077
| 0.157
| 0.234
| 0.305
| 0.370
| 0.426
| 0.472
| |
|
| 2.30
| 0.094
| 0.192
| 0.285
| 0.372
| 0.450
| 0.518
| 0.575
| |
|
| 2.45
| 0.109
| 0.221
| 0.329
| 0.430
| 0.520
| 0.599
| 0.665
| |
|
| 2.60
| 0.121
| 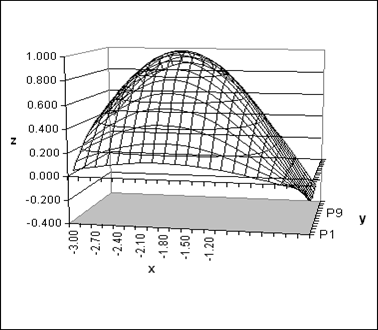 0.246 0.246
| 0.366
| 0.478
| 0.579
| 0.667
| 0.740
| |
|
| 2.75
| 0.130
| 0.266
| 0.395
| 0.515
| 0.624
| 0.719
| 0.798
| |
|
| 2.90
| 0.137
| 0.279
| 0.415
| 0.541
| 0.656
| 0.755
| 0.838
| |
|
| 3.05
| 0.141
| 0.286
| 0.426
| 0.555
| 0.673
| 0.775
| 0.860
| |
|
| 3.20
| 0.141
| 0.287
| 0.427
| 0.557
| 0.674
| 0.777
| 0.862
| |
|
| 3.35
| 0.138
| 0.281
| 0.418
| 0.546
| 0.661
| 0.761
| 0.845
| |
|
| 3.50
| 0.132
| 0.269
| 0.400
| 0.522
| 0.633
| 0.729
| 0.808
| |
|
| 3.65
| 0.123
| 0.251
| 0.373
| 0.487
| 0.590
| 0.680
| 0.754
| |
|
| 3.80
| 0.112
| 0.227
| 0.338
| 0.441
| 0.534
| 0.615
| 0.683
| |
|
| 3.95
| 0.097
| 0.199
| 0.295
| 0.385
| 0.467
| 0.537
| 0.596
| |
|
| 4.10
| 0.081
| 0.165
| 0.246
| 0.321
| 0.388
| 0.447
| 0.496
| |
|
| 4.25
| 0.063
| 0.128
| 0.191
| 0.249
| 0.301
| 0.347
| 0.385
| |
|
| 4.40
| 0.043
| 0.088
| 0.131
| 0.171
| 0.208
| 0.239
| 0.265
| |
|
| 4.55
| 0.023
| 0.046
| 0.069
| 0.090
| 0.109
| 0.126
| 0.140
| |
|
| 4.70
| 0.002
| 0.004
| 0.005
| 0.007
| 0.008
| 0.010
| 0.011
| |
|
| 4.85
| -0.019
| -0.039
| -0.059
| -0.077
| -0.093
| -0.107
| -0.118
| |
|
| 5.00
| -0.040
| -0.082
| -0.121
| -0.158
| -0.192
| -0.221
| -0.245
| Рис. 10 Построение поверхности.
Самостоятельная работа.
Построить график функций.
|
| 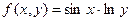 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом. , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом.
| 18.
|  , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| |
|  , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом. , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом.
| 19.
| 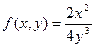 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| |
| 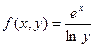 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 20.
| 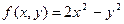 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| | 4.
| 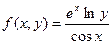 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 21.
| 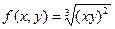 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| | 5.
| 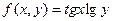 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 22.
| 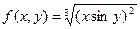 , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом , где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| | 6.
| 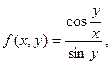 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом. где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом.
| 23.
| 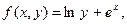 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом. где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом.
| | 7.
| 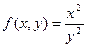 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 24.
| 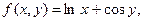 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом. где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом.
| | 8.
| 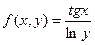 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 25.
| 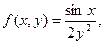 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| | 9.
| 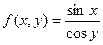 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 26.
|  где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| | 10.
|  где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же ша где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же ша
| 27.
| 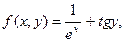 где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом
| | 11.
| 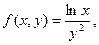 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же ша где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же ша
| 28.
|  где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же ша где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же ша
| | 12.
|  где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом
| 29.
| 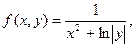 где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом
| | 13.
| 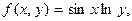 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 30.
| 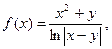 где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом
| | 14.
|  где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 31.
| 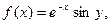 где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом где x изменяется от 2 до 10 с шагом 0, 15, а y– от -3 до 1, 2 с тем же шагом
| | 15.
| 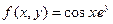 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 32.
| 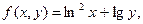 где y изменяется от 2 до 10 с шагом 0, 15, а x– от 3 до 12 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от 3 до 12 с тем же шагом
| | 16.
|  где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 33.
| 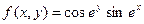 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| | 17.
| 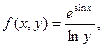 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
| 34.
| 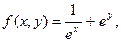 где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом где y изменяется от 2 до 10 с шагом 0, 15, а x– от -3 до 1, 2 с тем же шагом
|
Популярное:
|

