Двухстепенный роторный вибрационный гироскоп.
Схема двухстепенного роторного вибрационного гироскопа(РВГ) с несимметричным внутренним торсионным вращающимся подвесом представлена на рисунке 5.3.
На основании 1 установлен приводной двигатель 2, на валу 3 которого с помощью торсионов 4 укреплен ротор 5. С основанием связана система координат  (начало О – в точке пересечения осей вала и торсионов, ось
(начало О – в точке пересечения осей вала и торсионов, ось 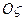 - ось вращения вала); с ротором связана система координат
- ось вращения вала); с ротором связана система координат  ( оси
( оси 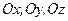 - главные центральные оси инерции, оси
- главные центральные оси инерции, оси  и
и  расположены в экваториальной плоскости ротора, ось
расположены в экваториальной плоскости ротора, ось  – ось торсионов). Основание вращается с абсолютной угловой скоростью, проекции которой на его оси составляют
– ось торсионов). Основание вращается с абсолютной угловой скоростью, проекции которой на его оси составляют 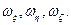 Торсионы 4, образующие подвес, имеют конечную жесткость на кручение вокруг оси
Торсионы 4, образующие подвес, имеют конечную жесткость на кручение вокруг оси  и существенно большую, практически равную бесконечности, жесткость на изгиб. Ротор 5 имеет две степени свободы относительно основания – вращается вместе с валом приводного двигателя с угловой скоростью
и существенно большую, практически равную бесконечности, жесткость на изгиб. Ротор 5 имеет две степени свободы относительно основания – вращается вместе с валом приводного двигателя с угловой скоростью 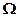 и может поворачиваться относительно вала вокруг вращающейся оси торсионов
и может поворачиваться относительно вала вокруг вращающейся оси торсионов  на угол
на угол 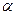 . При этом ротор поворачивается и вокруг осей основания
. При этом ротор поворачивается и вокруг осей основания  и
и 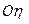 на углы
на углы 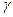 и
и  соответственно. Связь между углами
соответственно. Связь между углами 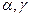 и
и  определяется соотношением
определяется соотношением
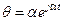 ,
, 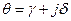 , (5.1)
, (5.1)
где 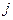 – мнимая единица.
– мнимая единица.
Для реализации режима измерения компоненты 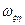 угловой скорости вращения основания, лежащей в плоскости осей
угловой скорости вращения основания, лежащей в плоскости осей  ,
,  и имеющей на эти оси проекции
и имеющей на эти оси проекции 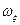 ,
,  , используются измерительные преобразователи 6 углов
, используются измерительные преобразователи 6 углов 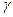 и
и  , управляющие сигналы которых через блоки усиления и обработки информации 7, включающие, в частности, усилители, фильтры и корректирующие звенья, поступают на преобразователи моментов 8, формирующие компенсационные моменты по осям
, управляющие сигналы которых через блоки усиления и обработки информации 7, включающие, в частности, усилители, фильтры и корректирующие звенья, поступают на преобразователи моментов 8, формирующие компенсационные моменты по осям  и
и  . Выходными сигналами РВГ являются падения напряжения на эталонных резисторах, включенных последовательно с управляющими обмотками преобразователей моментов, или управляющие напряжения
. Выходными сигналами РВГ являются падения напряжения на эталонных резисторах, включенных последовательно с управляющими обмотками преобразователей моментов, или управляющие напряжения 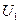 ,
, 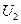 этих преобразователей.
этих преобразователей.
Сущность измерения РВГ угловой скорости основания заключается в следующем. При вращении основания с абсолютной угловой скоростью 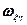 возникает гироскопический момент
возникает гироскопический момент 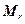 (рис. 5.3):
(рис. 5.3):
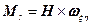 ,
, 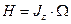 , (5.2)
, (5.2)
где 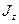 - момент инерции ротора относительно оси
- момент инерции ротора относительно оси 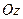 .
.
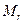 гармонически проектируется на ось торсионов
гармонически проектируется на ось торсионов  и порождает гармонические колебания ротора вокруг этой оси. В свою очередь в соответствии с (5.1) возникают угловые движения ротора по углам
и порождает гармонические колебания ротора вокруг этой оси. В свою очередь в соответствии с (5.1) возникают угловые движения ротора по углам 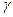 и
и  , несущие информацию об
, несущие информацию об 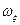 и
и  . Компенсационные моменты, развиваемые преобразователями моментов 8, парируют соответствующие гироскопические моменты по осям
. Компенсационные моменты, развиваемые преобразователями моментов 8, парируют соответствующие гироскопические моменты по осям  и
и  , а напряжения
, а напряжения 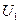 и
и 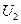 на входе преобразователей моментов пропорциональны соответственно
на входе преобразователей моментов пропорциональны соответственно 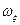 и
и  .
.
Действительно, полагая, что плоскость 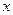 у ротора является плоскостью динамической симметрии, и для экваториальных главных моментов инерции относительно осей
у ротора является плоскостью динамической симметрии, и для экваториальных главных моментов инерции относительно осей  и
и  справедливо соотношение
справедливо соотношение 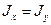 , опуская возмущающие моменты, приложенные к ротору, линеаризованную модель движения ротора по
, опуская возмущающие моменты, приложенные к ротору, линеаризованную модель движения ротора по 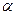 , который является малым, можно представить в следующем виде [70…73]:
, который является малым, можно представить в следующем виде [70…73]:
Jxα ″ +kα ′ +(c+ (Jz-Jx) Ω 2) α =H ω ξ sinΩ t-H ω η cosΩ t-Jx ω ′ ξ cosΩ t-
-Jx ω ′ η sinΩ t-2(Jz-Jx)Ω ω ζ α -ml(aξ sinΩ t-aη cosΩ t)+MДМξ cosΩ t +МДMη sinΩ t, (5.3)
где 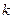 - коэффициент момента сил вязкого трения вокруг оси торсионов (определяется главным образом внутренним трением в подвесе);
- коэффициент момента сил вязкого трения вокруг оси торсионов (определяется главным образом внутренним трением в подвесе); 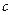 – угловая жесткость торсионов на кручение; m-масса ротора; l-смещение центра масс ротора вдоль оси Oz относительно неподвижной точки O; aξ , aη - проекции линейного ускорения основания соответственно на оси Oξ и Oη ;
– угловая жесткость торсионов на кручение; m-масса ротора; l-смещение центра масс ротора вдоль оси Oz относительно неподвижной точки O; aξ , aη - проекции линейного ускорения основания соответственно на оси Oξ и Oη ; 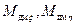 - моменты сил, формируемые преобразователями моментов вокруг осей
- моменты сил, формируемые преобразователями моментов вокруг осей  и
и  соответственно.
соответственно.
Непосредственно из анализа (5.3) следует, что выполнение условия
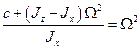 (5.4)
(5.4)
обеспечивает резонансное воздействие гироскопических моментов 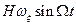 и
и 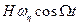 на ротор и, следовательно, обеспечивает большую крутизну преобразования измеряемых
на ротор и, следовательно, обеспечивает большую крутизну преобразования измеряемых 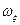 и
и  в амплитуду колебаний по
в амплитуду колебаний по 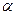 . Условие (5.4) можно переписать так:
. Условие (5.4) можно переписать так:
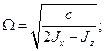 (5.5)
(5.5)
Условие (5.5) является условием резонансной динамической настройки РВГ. Следует отметить, что, поскольку в (5.3) динамическая составляющая жесткости 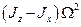 зависит от угловой скорости вращения вала
зависит от угловой скорости вращения вала  , крутизна преобразования
, крутизна преобразования 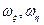 в амплитуду колебаний по
в амплитуду колебаний по 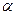 и соответствующая величина фазового сдвига не очень критичны к малым вариациям
и соответствующая величина фазового сдвига не очень критичны к малым вариациям  .
.
На основе (5.3), используя (5.1) и полагая 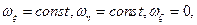 aξ = aη =0 нетрудно получить уравнения движения ротора вокруг осей корпуса
aξ = aη =0 нетрудно получить уравнения движения ротора вокруг осей корпуса 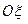 и
и  по углам
по углам 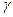 и
и  соответственно.
соответственно.
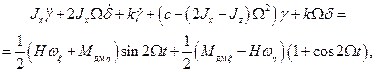 (5.6)
(5.6)
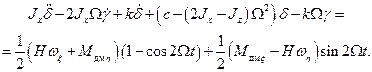
Заметим, что условие отсутствия в левых частях (5.6) позиционных членов совпадает с условием (5.5) резонансной настройки РВГ. Компенсационные моменты в (5.6) имеют вид:
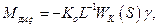
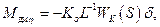 (5.7)
(5.7)
где 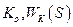 - коэффициент усиления и передаточная функция компенсационного канала (
- коэффициент усиления и передаточная функция компенсационного канала ( 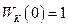 );
); 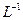 - символ обратного преобразования Лапласа.
- символ обратного преобразования Лапласа.
Из (5.6), (5.7), учитывая выполнение условия резонансной настройки (5.5) и малость вязкого трения в подвесе, для квазипостоянных составляющих  углов поворота ротора относительно корпуса в установившемся режиме получим:
углов поворота ротора относительно корпуса в установившемся режиме получим:
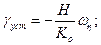
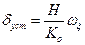 (5.8)
(5.8)
При этом, учитывая фактор подавления гармоник на частоте 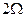 в заградительных фильтрах блоков 7 усиления и обработки информации (рис. 5.3), для выходных сигналов
в заградительных фильтрах блоков 7 усиления и обработки информации (рис. 5.3), для выходных сигналов 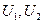 РВГ имеем:
РВГ имеем:
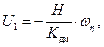
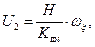 (5.9)
(5.9)
где  - коэффициент передачи преобразователя моментов по напряжению.
- коэффициент передачи преобразователя моментов по напряжению.
Остановимся теперь кратко на источниках основных погрешностей РВГ [5.4, 5.8]. К числу инструментальных погрешностей следует отнести погрешности, порождаемые поступательными и линейными вибрационными перегрузками основания при наличии у ротора статической несбалансированности – смещения его центра масс из неподвижной точки О вдоль осей 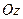 и
и  (рис. 5.3). Так, например как следует из анализа правой части уравнения (5.3), гармонические моменты сил инерции, порождаемые ускорениями aξ , aη структурно такие же и изменяются на той же частоте Ω, что и «информационные» гармонические гироскопические моменты, порождаемые измеряемыми угловыми скоростями
(рис. 5.3). Так, например как следует из анализа правой части уравнения (5.3), гармонические моменты сил инерции, порождаемые ускорениями aξ , aη структурно такие же и изменяются на той же частоте Ω, что и «информационные» гармонические гироскопические моменты, порождаемые измеряемыми угловыми скоростями 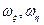 . Поэтому при наличии l ускорения aξ , aη порождают аддитивные погрешности РВГ. Влияние динамической неуравновешенности на погрешности РВГ проявляется главным образом при неравножесткости опор главного вращения.
. Поэтому при наличии l ускорения aξ , aη порождают аддитивные погрешности РВГ. Влияние динамической неуравновешенности на погрешности РВГ проявляется главным образом при неравножесткости опор главного вращения.
Инструментальные погрешности РВГ имеют место также при нарушении условий резонансной динамической настройки (5.5) - при расстройке ИЧЭ вследствие отклонения параметров РВГ от их номинальных величин. Расстройка 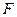 РВГ определяется разностью между его собственной динамической частотой
РВГ определяется разностью между его собственной динамической частотой
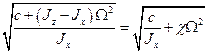 , где
, где 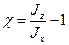 , (5.10)
, (5.10)
и угловой скоростью вращения вала  .
.
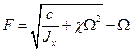 (5.11)
(5.11)
Приращение расстройки Δ F при отклонении параметров РВГ от номинальных значений можно приближенно представить в виде полного дифференциала функции 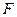
Δ F=(∂ F∕ ∂ c)0 ∆ c + (∂ F∕ ∂ Ω )0 ∆ Ω + (∂ F∕ ∂ χ )0 ∆ χ , (5.12)
где Δ c, Δ Ω, Δ χ - вариации угловой жесткости торсионов на кручение, угловой скорости вращения вала, параметра 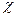 соответственно; индекс
соответственно; индекс 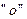 у частных производных означает, что их следует вычислять при значениях
у частных производных означает, что их следует вычислять при значениях 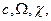 равных номинальным.
равных номинальным.
Подставляя (5.11) в (5.12) и учитывая тот факт, что при номинальных 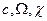 выполняется условие (5.5), получим:
выполняется условие (5.5), получим:
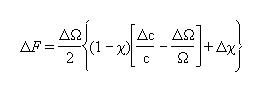
(5.13)
Согласно (5.13) для уменьшения расстройки следует обеспечивать равенство 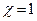 , однако точное выполнение этого условия невозможно вследствие того, что
, однако точное выполнение этого условия невозможно вследствие того, что 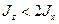 . На практике параметр
. На практике параметр 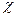 достигает 0, 97.
достигает 0, 97.
Существенным фактором, ограничивающим точностные характеристики РВГ, является температурный дрейф его нулевого сигнала, порождаемый при вариациях температуры относительно номинальной не только расстройкой Δ F, но и смещением ² нулей² измерительных преобразователей углов и электронных блоков, изменением крутизны измерительных преобразователей углов и преобразователей моментов, а также другими факторами, обусловленными взаимосвязанными механическими, теплообменными и термоупругими процессами [5.9]. Уменьшение температурных погрешностей РВГ достигается за счет их алгоритмической компенсации, реализуемой на основе предварительной калибровки параметров моделей погрешностей, а также за счет повышения коэффициента передачи гироскопа как произведения коэффициентов передачи его механической части от моментов к углу 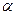 (согласно (5.3)), крутизн измерительных преобразователей и преобразователей моментов. [5.10].
(согласно (5.3)), крутизн измерительных преобразователей и преобразователей моментов. [5.10].
Методические погрешности РВГ порождаются проекцией 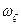 абсолютной угловой скорости основания на ось вращения приводного двигателя. Наличие
абсолютной угловой скорости основания на ось вращения приводного двигателя. Наличие 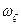 согласно (5.3) приводит фактически к изменению угловой жесткости подвеса, а следовательно к нарушению условия резонансной динамической настройки. Методические погрешности порождаются также проекциями угловых ускорений основания
согласно (5.3) приводит фактически к изменению угловой жесткости подвеса, а следовательно к нарушению условия резонансной динамической настройки. Методические погрешности порождаются также проекциями угловых ускорений основания 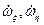 на оси РВГ. Наиболее существенная методическая погрешность РВГ порождается угловыми вибрациями основания вокруг осей
на оси РВГ. Наиболее существенная методическая погрешность РВГ порождается угловыми вибрациями основания вокруг осей 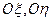 на частоте
на частоте 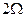 . Действительно, положим, например, в (5.3)
. Действительно, положим, например, в (5.3)
aξ = aη = 0, 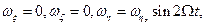 где
где 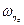 - амплитуда угловой вибрации. Имеют место соотношения:
- амплитуда угловой вибрации. Имеют место соотношения:
 ,
,
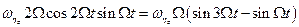 (5.14)
(5.14)
Подставляя (5.14) в правую часть (5.3), получим:
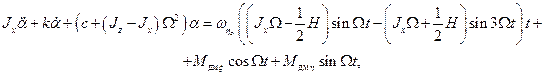 (5.15)
(5.15)
Из сравнения правых частей (5.3) и (5.15) следует, что угловая вибрация на частоте 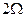 порождает гироскопический момент
порождает гироскопический момент 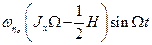 , аналогичный моменту
, аналогичный моменту 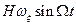 , создаваемому измеряемой квазипостоянной компонентой угловой скорости
, создаваемому измеряемой квазипостоянной компонентой угловой скорости 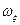 .
.
Рассмотренные факторы методического характера предопределяют сравнительно невысокую точность РВГ. Характерные параметры РВГ, работающего в режиме датчика угловой скорости (ДУС), представлены в таблице 5.1.
Существенно более высокоточным ДНГ, в котором за счет динамической настройки ротор освобождается от упругих связей с валом приводного двигателя, является ДНГ с двухколечным упругим подвесом.
Популярное:

