закон сохранения мех энергии системы матер точек
Закон сохранения механической энергии системы материальных точек.
Рассмотрим систему, состоящую из n материальных точек, между которыми действуют консервативные силы внутреннего взаимодействия  , и кроме того на материальные точки действуют внешние консервативные силы
, и кроме того на материальные точки действуют внешние консервативные силы  и внешние неконсервативные силы
и внешние неконсервативные силы  .
.
Для каждой материальной точки запишем второй закон Ньютона:
 ,
,
 ,
,
 .
.
Далее левые и правые части каждого уравнения умножим скалярно на  , соответственно, где
, соответственно, где 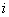 – номер материальной точки. Покажем это на примере
– номер материальной точки. Покажем это на примере 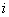 -ой материальной точки:
-ой материальной точки:

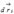 ,
,
 .
.
Это равенство можно записать в виде:
 , или
, или  ,
,
где  – кинетическая энергия
– кинетическая энергия 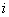 -ой материальной точки,
-ой материальной точки,
 – внутренняя потенциальная энергия
– внутренняя потенциальная энергия 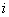 -ой материальной точки,
-ой материальной точки,
 – внешняя потенциальная энергия
– внешняя потенциальная энергия 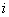 -ой материальной точки,
-ой материальной точки,
 – работа, которую совершают над
– работа, которую совершают над 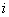 -ой материальной точкой внешняя неконсервативная сила.
-ой материальной точкой внешняя неконсервативная сила.
Просуммируем левые и правые части преобразованных указанным образом уравнений движения.
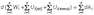 ,
,
или  ,
,
где 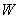 – кинетическая энергия системы материальных точек,
– кинетическая энергия системы материальных точек,
 ,
,  – внутренняя и внешняя потенциальная энергия м.т.,
– внутренняя и внешняя потенциальная энергия м.т.,
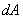 – полная работа внешних неконсервативных сил.
– полная работа внешних неконсервативных сил.
Если внешние неконсервативные силы отсутствуют, правая часть полученного уравнения будет равна нулю и, следовательно, полная механическая энергия системы остается постоянной:
 - закон сохранения механической энергии системы материальных точек.
- закон сохранения механической энергии системы материальных точек.
Полная механическая энергия системы материальных точек, на которые действуют лишь консервативные силы, остается постоянной, т.е. сохраняется во времени.
Для замкнутой системы закон сохранения полной механической энергии имеет вид:
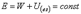 .
.
Полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной, т.е. сохраняется во времени.
Если в замкнутой системе, кроме консервативных, действуют такие неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Те системы, по отношению к которым выполняется первый закон Ньютона, называются инерциальными системами отсчета.
12. момент импульса частицы. Момент Силы
Момент импульса материальной точки (частицы) относительно точки О - векторная величина 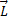 = [
= [ 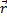 ,
,  ] = [
] = [ 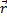 ,
,  ], где r – радиус-вектор, определяющий положение частицы относительно точки O, а p=mv – импульс частицы. Модуль L, равный rp
], где r – радиус-вектор, определяющий положение частицы относительно точки O, а p=mv – импульс частицы. Модуль L, равный rp  , можно представить в виде произведения плеча импульса l на модуль вектора p: L = lp. Частица обладает моментом импульса независимо от формы траектории, по которой она движется. Если она движется вдоль прямолинейной траектории, L=mvl, если частица движется по окружности радиуса r, L=mvr. Модуль L может изменяться только за счет изменения модуля скорости. Несмотря на непрерывное изменение направления вектора p, направление вектора L остается постоянным. Проекция вектора L на произвольную ось, проходящую через точку О, - моментом импульса частицы относительно этой оси. Производная по времени от момента импульса относительно оси равна моменту относительно той же оси сил, действующих на частицу. Скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на частицу
, можно представить в виде произведения плеча импульса l на модуль вектора p: L = lp. Частица обладает моментом импульса независимо от формы траектории, по которой она движется. Если она движется вдоль прямолинейной траектории, L=mvl, если частица движется по окружности радиуса r, L=mvr. Модуль L может изменяться только за счет изменения модуля скорости. Несмотря на непрерывное изменение направления вектора p, направление вектора L остается постоянным. Проекция вектора L на произвольную ось, проходящую через точку О, - моментом импульса частицы относительно этой оси. Производная по времени от момента импульса относительно оси равна моменту относительно той же оси сил, действующих на частицу. Скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на частицу
Момент силы относительно точки О - вектор  , модуль которого равен произведению модуля силы
, модуль которого равен произведению модуля силы  на её плечо: M = Fl=Fr
на её плечо: M = Fl=Fr  . Плечом силы называют длину перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила. Вектор
. Плечом силы называют длину перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила. Вектор  направлен перпендикулярно плоскости, в которой лежат сила и точка О, направление определяется по правилу буравчика. Модуль и направление момента силы
направлен перпендикулярно плоскости, в которой лежат сила и точка О, направление определяется по правилу буравчика. Модуль и направление момента силы  совпадают с модулем и направлением векторного произведения векторов
совпадают с модулем и направлением векторного произведения векторов 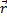 и
и  . Поэтому:
. Поэтому:  = [
= [ 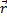 ,
,  ], где
], где 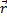 – радиус-вектор точки приложения силы, проведенный из точки, относительно которой определяется момент. Когда сила приложена к одной из точек твердого тела, вектор
– радиус-вектор точки приложения силы, проведенный из точки, относительно которой определяется момент. Когда сила приложена к одной из точек твердого тела, вектор  характеризует способность силы вращать тело вокруг точки О, относительно которой он берется. Поэтом момент силы - вращающий момент. Под действием силы тело повернется вокруг оси, совпадающей с направлением вращающего момента. Проекция вектора
характеризует способность силы вращать тело вокруг точки О, относительно которой он берется. Поэтом момент силы - вращающий момент. Под действием силы тело повернется вокруг оси, совпадающей с направлением вращающего момента. Проекция вектора  на произвольную ось – момент силы относительно этой оси, характеризует способность тела вращаться вокруг этой оси. Две равные по модулю, противоположно направленные силы, не действующие вдоль одной прямой – пара сил. Расстояние между прямыми, вдоль которых действуют силы – плечо пары l. Суммарный момент сил относительно точки О:
на произвольную ось – момент силы относительно этой оси, характеризует способность тела вращаться вокруг этой оси. Две равные по модулю, противоположно направленные силы, не действующие вдоль одной прямой – пара сил. Расстояние между прямыми, вдоль которых действуют силы – плечо пары l. Суммарный момент сил относительно точки О:  = [
= [  ] = [
] = [ 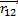 ,
, 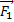 ], т.к.
], т.к.  = -
= - 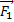 . Моменты внутренних сил, попарно уравновешивают друг друга, сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю.
. Моменты внутренних сил, попарно уравновешивают друг друга, сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю.
13. Уравнение динамики вращательного движения твердого тела. Момент инерции.
Пусть F – сила, приложенная в точке B, находящейся на расстоянии r,  – угол между направлением силы и радиус-вектором r. Т. К тело абсолютно твердое, работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d
– угол между направлением силы и радиус-вектором r. Т. К тело абсолютно твердое, работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол d  точка приложения b проходит путь ds = rd
точка приложения b проходит путь ds = rd  и работа равна произведению проекции силы на направление смещения на величину смещения: dA=F
и работа равна произведению проекции силы на направление смещения на величину смещения: dA=F  =
=  d
d  - момент силы относительно оси Z. Работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но dT=d
- момент силы относительно оси Z. Работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но dT=d  поэтому
поэтому  =
=  или
или 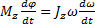 . Учитывая, что
. Учитывая, что  получаем
получаем  .
.
Это уравнение динамики вращательного движения твердого тела относительно оси. Если ось Z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство: 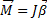 , где J – главный момент инерции тела (момент инерции относительно главной оси).
, где J – главный момент инерции тела (момент инерции относительно главной оси).
Момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси:  Так как центр масс твердого тела представляет собой точку с радиус-вектором:
Так как центр масс твердого тела представляет собой точку с радиус-вектором:  Поскольку выражение является не вполне однозначным, так как каждый их векторов
Поскольку выражение является не вполне однозначным, так как каждый их векторов  можно проводить в любую из точек i-ой элементарной массы, нужно взять предел выражения при условии что все
можно проводить в любую из точек i-ой элементарной массы, нужно взять предел выражения при условии что все  стремятся к нулю. Так же суммирование в выражении для момента инерции должно быть заменено интегрированием:
стремятся к нулю. Так же суммирование в выражении для момента инерции должно быть заменено интегрированием:
 , т.к. dm=
, т.к. dm= 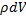
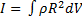 , где
, где  - плотность тела в точке, в которой взят объем dV, R –расстояние этого объема от оси, относительно которой вычисляется момент. Если тело однородно, плотность во всех его точках одинакова, то
- плотность тела в точке, в которой взят объем dV, R –расстояние этого объема от оси, относительно которой вычисляется момент. Если тело однородно, плотность во всех его точках одинакова, то  .
.
Найдем момент инерции однородного цилиндра относительно его геометрической оси OO. Разобьем цилиндр на слои радиуса R и толщины dR, Масса такого слоя равна  , dV – объем такого слоя. Все точки слоя отстоят от оси ОО на одинаковое расстояние R. Поэтому вклад слоя в момент инерции равен:
, dV – объем такого слоя. Все точки слоя отстоят от оси ОО на одинаковое расстояние R. Поэтому вклад слоя в момент инерции равен: 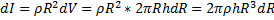 . Проинтегрировав это выражение по R в пределах от 0 до r (радиус цилиндра), получим искомый момент инерции:
. Проинтегрировав это выражение по R в пределах от 0 до r (радиус цилиндра), получим искомый момент инерции: 
14. Теорема Штейнера
Рассмотрим произвольное тело и две параллельные друг другу оси, одна из которых (ось С) проходит через центр масс тела, а другая (ось О) отстоит от первой на расстояние 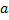 . Выберем оси координат x, y,
. Выберем оси координат x, y, 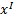 ,
,  . Момент инерции I относительно оси О определяется выражением:
. Момент инерции I относительно оси О определяется выражением: 
Разобьем это выражение на три суммы:  . Первая сумма представляет собой момент инерции
. Первая сумма представляет собой момент инерции  оси, проходящей через центр масс. Сумма
оси, проходящей через центр масс. Сумма 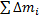 дает массу тела m, а
дает массу тела m, а  =
= 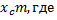
 - координата центр масс, которая при сделанном выборе начала координат равна нулю. Так, мы приходим к соотношению:
- координата центр масс, которая при сделанном выборе начала координат равна нулю. Так, мы приходим к соотношению: 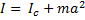 . Это соотношение выражает теорему Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. Момент инерции однородного цилиндра относительно оси, совпадающей с образующей цилиндра:
. Это соотношение выражает теорему Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. Момент инерции однородного цилиндра относительно оси, совпадающей с образующей цилиндра: 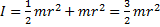 Момент инерции тонкого стержня (максимальный поперечный размер его много меньше длины) относительно перпендикулярной к нему оси, проходящей через его конец:
Момент инерции тонкого стержня (максимальный поперечный размер его много меньше длины) относительно перпендикулярной к нему оси, проходящей через его конец:  Момент инерции стержня относительно перпендикулярной к нему оси, проходящей через его центр:
Момент инерции стержня относительно перпендикулярной к нему оси, проходящей через его центр:  , где
, где  Момент инерции однородного шара относительно оси, проходящей через его центр:
Момент инерции однородного шара относительно оси, проходящей через его центр: 
15. Закон сохранения момента импульса системы материальных точек.
Рассмотрим систему частиц, на которые действуют как внутренние, так и внешние силы. Момент импульса системы относительно точки O – сумма моментов импульса 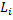 отдельных частиц:
отдельных частиц: 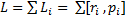 . Дифференцирование по времени дает, что
. Дифференцирование по времени дает, что  . Поэтому для каждой из частиц:
. Поэтому для каждой из частиц:  , где
, где 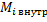 - момент внутренних сил,
- момент внутренних сил,  - момент внешних сил, действующих на i-ую частицу. Получаем:
- момент внешних сил, действующих на i-ую частицу. Получаем:  Каждое их слагаемых – сумма моментов сил, действующих на i-ую частицу. Если перейти к суммированию сил независимо от того, к какой из частиц они приложены, индекс I в суммах можно опустить. Т.к. суммарный момент внутренних сил равен нулю, получаем:
Каждое их слагаемых – сумма моментов сил, действующих на i-ую частицу. Если перейти к суммированию сил независимо от того, к какой из частиц они приложены, индекс I в суммах можно опустить. Т.к. суммарный момент внутренних сил равен нулю, получаем: 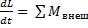 - производная по времени от момента импульса системы равна сумме моментов внешних сил. Спроектировав векторы на произвольную ось Z, проходящую через точку О, получим:
- производная по времени от момента импульса системы равна сумме моментов внешних сил. Спроектировав векторы на произвольную ось Z, проходящую через точку О, получим:  Если система замкнута (т.е. внешних сил нет),
Если система замкнута (т.е. внешних сил нет),  , значит вектор L не изменяется со временем. Отсюда вытекает закон сохранения момента импульса: момент импульса замкнутой системы материальных точек остается постоянным. Будет постоянным и момент импульса замкнутой системы относительно любой оси, проходящей через точку О. Момент импульса сохраняется и для незамкнутой системы, если сумма моментов внешних сил равна нулю. Момент импульса системы относительно оси Z сохраняется при условии, что сумма моментов внешних сил относительно этой оси равна нулю.
, значит вектор L не изменяется со временем. Отсюда вытекает закон сохранения момента импульса: момент импульса замкнутой системы материальных точек остается постоянным. Будет постоянным и момент импульса замкнутой системы относительно любой оси, проходящей через точку О. Момент импульса сохраняется и для незамкнутой системы, если сумма моментов внешних сил равна нулю. Момент импульса системы относительно оси Z сохраняется при условии, что сумма моментов внешних сил относительно этой оси равна нулю.
16. Кинетическая энергия тела, вращающегося вокруг неподвижной оси. Работа внешних сил при вращении твердого тела вокруг неподвижной оси
Когда тело вращается вокруг неподвижной оси с угловой скоростью  , элементарная масса
, элементарная масса  , отстоящая от оси вращения на расстояние
, отстоящая от оси вращения на расстояние 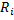 , обладает скоростью
, обладает скоростью  . Следовательно, ее кинетическая энергия равна:
. Следовательно, ее кинетическая энергия равна:  Сумма энергий
Сумма энергий  даст кинетическую энергию всего тела:
даст кинетическую энергию всего тела:  .Т.к.
.Т.к.  , получаем выражение:
, получаем выражение:  . Это выражение аналогично выражению для кинетической энергии материальной точки (и поступательно движущегося тела). Роль массы играет момент инерции, роль линейной скорости – угловая скорость. Найдем работу, совершаемую внешней силой при вращении твердого тела. Если сила направлена по касательной к окружности, по которой движется точка приложения силs, сила F и перемещение dS точки ее приложения коллинеарны. Элементарная работа
. Это выражение аналогично выражению для кинетической энергии материальной точки (и поступательно движущегося тела). Роль массы играет момент инерции, роль линейной скорости – угловая скорость. Найдем работу, совершаемую внешней силой при вращении твердого тела. Если сила направлена по касательной к окружности, по которой движется точка приложения силs, сила F и перемещение dS точки ее приложения коллинеарны. Элементарная работа  . Если сила действует в направлении перемещения,
. Если сила действует в направлении перемещения,  равна модулю силы F и
равна модулю силы F и  . Если сила и перемещение направлены в противоположные стороны,
. Если сила и перемещение направлены в противоположные стороны,  и
и  . Оба выражения для работы можно заменить одной формулой:
. Оба выражения для работы можно заменить одной формулой:  , ее можно представить в виде:
, ее можно представить в виде:  , т.к. направления оси Z и вектора
, т.к. направления оси Z и вектора  совпадают, где
совпадают, где  - проекция вектора M на направление вектора
- проекция вектора M на направление вектора  . Эта формула сходна с формулой
. Эта формула сходна с формулой  , также если написать ее в виде
, также если написать ее в виде  , где
, где  - проекция силы F на направление скорости
- проекция силы F на направление скорости  точки приложения силы (направления векторов
точки приложения силы (направления векторов  и dS совпадают)
и dS совпадают)
17. Основные представления дорелятивистской физики, её противоречия
В классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета. Рассмотрим две системы отсчета: инерциальная K с координатами (x, y, z), ее условно будем считать неподвижной, и систему 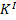 , движущуюся относительно K равномерно и прямолинейно со скоростью u=const. Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Скорость направлена вдоль
, движущуюся относительно K равномерно и прямолинейно со скоростью u=const. Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Скорость направлена вдоль  , радиус-вектор, проведенный из
, радиус-вектор, проведенный из  ,
, 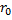 =ut. Связь между координатами произвольной точки А в обеих системах:
=ut. Связь между координатами произвольной точки А в обеих системах:  . Это можно записать в проекциях на оси координат:
. Это можно записать в проекциях на оси координат:  ,
,  ,
, 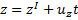 . Эти уравнения носят название преобразований координат Галилея. Когда система
. Эти уравнения носят название преобразований координат Галилея. Когда система 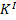 движется со скоростью
движется со скоростью  вдоль положительного направления оси X системы К (в начальный момент времени оси координат совпадают), преобразования имеют вид:
вдоль положительного направления оси X системы К (в начальный момент времени оси координат совпадают), преобразования имеют вид:  ,
,  ,
,  . В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, т.е. можно добавить еще одно уравнение:
. В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, т.е. можно добавить еще одно уравнение:  . Записанные соотношения справедливы лишь в случае классической механики (u< < c). Продифференцировав по времени, получим: v=
. Записанные соотношения справедливы лишь в случае классической механики (u< < c). Продифференцировав по времени, получим: v=  + u – это правило сложения скоростей в классической механике. Ускорение в системе отсчета К:
+ u – это правило сложения скоростей в классической механике. Ускорение в системе отсчета К:
 . Так ускорение точки А в системах отсчета
. Так ускорение точки А в системах отсчета 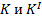 , движущихся друг относительно друга равномерно и прямолинейно, одинаково:
, движущихся друг относительно друга равномерно и прямолинейно, одинаково: 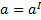 . Следовательно, если на точку другие тела не действуют (а=0), то
. Следовательно, если на точку другие тела не действуют (а=0), то  , т.е. система
, т.е. система 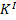 является инерциальной (точка движется относительно неравномерно и прямолинейно или покоится). Отсюда вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными. Галилей обратил внимание на то, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится она или движется равномерно и прямолинейно.
является инерциальной (точка движется относительно неравномерно и прямолинейно или покоится). Отсюда вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными. Галилей обратил внимание на то, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится она или движется равномерно и прямолинейно.
18. Постулаты Эйнштейна. Синхронизация часов, соотношения между событиями
Движение тел, обладающих большими скоростями, а также распространение света не подчиняются законам классической механики. Эйнштейн пришел к выводу, что мирового эфира – особой среды, которая могла бы быть принята в качестве абсолютной системы, - не существует. Существование постоянной скорости распространения света в вакууме находилось в согласии с уравнениями Максвелла для электромагнитного поля. Эйнштейн заложил основы СТО (специальная теория относительности или релятивистская), в которой предполагается, что время однородно, пространство однородно и изотропно (нет выделенных направлений). В основе СТО постулаты Эйнштейна: 1) принцип относительности: никакие опыты, проведенные внутри данной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой – обобщение механического принципа относительности на любые физические процессы: физ законы инвариантны по отношению к выбору инерциальной системы отсчета, уравнения, описывающие эти законы, одинаковы по форме во всех инерц системах отсчета, все инерц системы отсчета равноправны, явления (механические, электродинамические, оптические и др.) протекают одинаково во всех инерц системах отсчета. 2) принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета – фундаментальное свойство природы как опытный факт. В СТО постулируется возможность определения единого времени в рамках данной инерциальной системы отсчёта. Для этого вводится процедура синхронизации двух часов, находящихся в различных точках ИСО. Пусть от первых часов, в момент времени  ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью
ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью 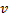 . Сразу по достижении вторых часов (по их показаниям в момент времени T) сигнал отправляется обратно с той же постоянной скоростью
. Сразу по достижении вторых часов (по их показаниям в момент времени T) сигнал отправляется обратно с той же постоянной скоростью  и достигает первых часов в момент времени
и достигает первых часов в момент времени 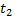 . Часы считаются синхронизированными, если выполняется соотношение
. Часы считаются синхронизированными, если выполняется соотношение  . Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых неподвижных относительно друг друга часов, так что справедливо свойство транзитивности: если часы A синхронизованы с часами B, а часы B синхронизованы с часами C, то часы A и C также окажутся синхронизованными. В отличие от классической механики единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.
. Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых неподвижных относительно друг друга часов, так что справедливо свойство транзитивности: если часы A синхронизованы с часами B, а часы B синхронизованы с часами C, то часы A и C также окажутся синхронизованными. В отличие от классической механики единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.
19. Замедление движущихся часов и сокращение продольных размеров движущихся тел
Если часы неподвижны в системе 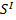 , то для двух последовательных событий имеет место
, то для двух последовательных событий имеет место  . Такие часы перемещаются относительно системы S по закону
. Такие часы перемещаются относительно системы S по закону  , поэтому интервалы времени связаны следующим образом:
, поэтому интервалы времени связаны следующим образом: 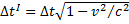 . Важно понимать, что в этой формуле интервал времени
. Важно понимать, что в этой формуле интервал времени  измеряется одними движущимися часами. Он сравнивается с показаниями
измеряется одними движущимися часами. Он сравнивается с показаниями  нескольких различных, синхронно идущих часов, расположенных в системе S, мимо которых движутся часы
нескольких различных, синхронно идущих часов, расположенных в системе S, мимо которых движутся часы 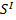 . В результате такого сравнения оказывается, что движущиеся часы
. В результате такого сравнения оказывается, что движущиеся часы 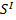 идут медленнее неподвижных часов. С этим эффектом связан так называемый парадокс близнецов.Если часы движутся с переменной скоростью
идут медленнее неподвижных часов. С этим эффектом связан так называемый парадокс близнецов.Если часы движутся с переменной скоростью 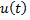 относительно инерциальной системы отсчёта, то время, измеряемое этими часами (т. н. собственное время), не зависит от ускорения, и может быть вычислено по следующей формуле:
относительно инерциальной системы отсчёта, то время, измеряемое этими часами (т. н. собственное время), не зависит от ускорения, и может быть вычислено по следующей формуле:  , где при помощи интегрирования, суммируются интервалы времени в локально инерциальных системах отсчёта. Если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся системе отсчёта
, где при помощи интегрирования, суммируются интервалы времени в локально инерциальных системах отсчёта. Если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся системе отсчёта 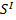 , то они будут неодновременны относительно «неподвижной» системы S. При
, то они будут неодновременны относительно «неподвижной» системы S. При  из преобразований Лоренца следует
из преобразований Лоренца следует 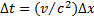 Если
Если 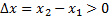 , то и
, то и 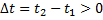 . Это означает, что, с точки зрения неподвижного наблюдателя, левое событие происходит раньше правого
. Это означает, что, с точки зрения неподвижного наблюдателя, левое событие происходит раньше правого 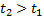 . Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве. Пусть в двух системах отсчёта, вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов они показывают одинаковое время. Первый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают «центральные» часы. Аналогична ситуация для наблюдателей в S' (второй рисунок).
. Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве. Пусть в двух системах отсчёта, вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов они показывают одинаковое время. Первый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают «центральные» часы. Аналогична ситуация для наблюдателей в S' (второй рисунок). 
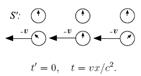
Если длину (форму) движущегося объекта определять при помощи одновременной фиксации координат его поверхности, то из преобразований Лоренца следует, что линейные размеры такого тела относительно «неподвижной» системы отсчёта сокращаются:  , где
, где  — длина вдоль направления движения относительно неподвижной системы отсчёта, а
— длина вдоль направления движения относительно неподвижной системы отсчёта, а 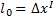 — длина в движущейся системе отсчёта, связанной с телом (собственная длина тела). При этом сокращаются продольные размеры тела (то есть измеряемые вдоль направления движения). Поперечные размеры не изменяются.Такое сокращение размеров ещё называют лоренцевым сокращением. При визуальном наблюдении движущихся тел, дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит повёрнутым, но не сжатым в направлении движения.
— длина в движущейся системе отсчёта, связанной с телом (собственная длина тела). При этом сокращаются продольные размеры тела (то есть измеряемые вдоль направления движения). Поперечные размеры не изменяются.Такое сокращение размеров ещё называют лоренцевым сокращением. При визуальном наблюдении движущихся тел, дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит повёрнутым, но не сжатым в направлении движения.
20. Преобразования Лоренца
Рассмотрим две инерц системы отсчета: 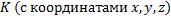 и
и  , движущуюся относительно K (вдоль оси x) со скоростью v=const. Пусть в начальный момент времени
, движущуюся относительно K (вдоль оси x) со скоростью v=const. Пусть в начальный момент времени  , когда начала
, когда начала  совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одна и та же и равна
совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одна и та же и равна  . Поэтому, если за время tв системе
. Поэтому, если за время tв системе  сигнал дойдет до некоторой точки
сигнал дойдет до некоторой точки  , пройдя расстояние
, пройдя расстояние 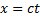 , то в системе
, то в системе  координата светового импульса в момент достижения точки
координата светового импульса в момент достижения точки  :
:  , где
, где  - время прохождения светового импульса от начала координат до точки
- время прохождения светового импульса от начала координат до точки  в системе
в системе  . Вычитая, получаем:
. Вычитая, получаем:  . Т.к.
. Т.к. 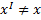 (система
(система  перемещается по отношению к системе K), то
перемещается по отношению к системе K), то 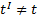 , т.е. отсчет времени в системах K и
, т.е. отсчет времени в системах K и  различен – отсчет времени имеет относительный характер, в отличие от классич механики. Эйнштейн показал, что в теории относительности классич преобразования Галилея, описывающие переход от одной инерциальной системы отсчета к другой, заменяются преобразованиями Лоренца (предложенные до появления теории относительности как преобразования, относительно которых уравнения Максвелла инвариантны), удовлетворяющими постулатам Эйнштейна:
различен – отсчет времени имеет относительный характер, в отличие от классич механики. Эйнштейн показал, что в теории относительности классич преобразования Галилея, описывающие переход от одной инерциальной системы отсчета к другой, заменяются преобразованиями Лоренца (предложенные до появления теории относительности как преобразования, относительно которых уравнения Максвелла инвариантны), удовлетворяющими постулатам Эйнштейна:  :
:  ,
, 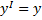 ,
, 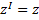 ,
, 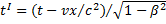 ;
; 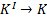 :
:  ,
,  ,
,  ,
, 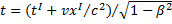 , где
, где  . Приведенные уравнения симметричны, т.к. если скорость движение системы
. Приведенные уравнения симметричны, т.к. если скорость движение системы 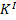 относительно
относительно  равна
равна  , то скорость движение системы
, то скорость движение системы  относительно
относительно 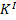 равна
равна  . При малых скоростях (
. При малых скоростях (  ), т.е. когда
), т.е. когда  , они переходят в классические преобразования Галилея (суть принципа соответствия) как предельный случай преобразований Лоренца. При
, они переходят в классические преобразования Галилея (суть принципа соответствия) как предельный случай преобразований Лоренца. При  выражения теряют свой физ смысл, т.к. движение со скоростью, большей скорости распространения света в вакууме, невозможно. Как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерц сист отсчета к другой, теория Эйнштейна рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.
выражения теряют свой физ смысл, т.к. движение со скоростью, большей скорости распространения света в вакууме, невозможно. Как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерц сист отсчета к другой, теория Эйнштейна рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.
21. Следствия преобразований Лоренца
1. сложение скоростей: если некоторый объект имеет компоненты скорости  относительно системы S и
относительно системы S и  — относительно S', то между ними существует следующая связь:
— относительно S', то между ними существует следующая связь:  ,
, 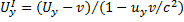 ,
,  В этих соотношениях относительная скорость движения систем отсчёта
В этих соотношениях относительная скорость движения систем отсчёта  направлена вдоль оси x. Релятивистское сложение скоростей, как и преобразования Лоренца, при малых скоростях (
направлена вдоль оси x. Релятивистское сложение скоростей, как и преобразования Лоренца, при малых скоростях (  ) переходит в классический закон сложения скоростей.Если объект движется со скоростью света
) переходит в классический закон сложения скоростей.Если объект движется со скоростью света  вдоль оси x относительно системы S, то такая же скорость у него будет и относительно S':
вдоль оси x относительно системы S, то такая же скорость у него будет и относительно S':  . Это означает, что скорость
. Это означает, что скорость 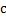 является инвариантной (одинаковой) во всех инерц сист отсчета. 2. замедление времени: если часы неподвижны в системе
является инвариантной (одинаковой) во всех инерц сист отсчета. 2. замедление времени: если часы неподвижны в системе 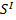 , то для двух последовательных событий имеет место
, то для двух последовательных событий имеет место  . Такие часы перемещаются относительно системы S по закону
. Такие часы перемещаются относительно системы S по закону  , поэтому интервалы времени связаны следующим образом:
, поэтому интервалы времени связаны следующим образом: 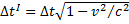 . Важно понимать, что в этой формуле интервал времени
. Важно понимать, что в этой формуле интервал времени  измеряется одними движущимися часами. Он сравнивается с показаниями
измеряется одними движущимися часами. Он сравнивается с показаниями  нескольких различных, синхронно идущих часов, расположенных в системе S, мимо которых движутся часы
нескольких различных, синхронно идущих часов, расположенных в системе S, мимо которых движутся часы 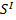 . В результате такого сравнения оказывается, что движущиеся часы
. В результате такого сравнения оказывается, что движущиеся часы 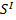 идут медленнее неподвижных часов. С этим эффектом связан так называемый парадокс близнецов.Если часы движутся с переменной скоростью
идут медленнее неподвижных часов. С этим эффектом связан так называемый парадокс близнецов.Если часы движутся с переменной скоростью 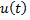 относительно инерциальной системы отсчёта, то время, измеряемое этими часами (т. н. собственное время), не зависит от ускорения, и может быть вычислено по следующей формуле:
относительно инерциальной системы отсчёта, то время, измеряемое этими часами (т. н. собственное время), не зависит от ускорения, и может быть вычислено по следующей формуле:  , где при помощи интегрирования, суммируются интервалы времени в локально инерциальных системах отсчёта. 3) Относительность одновременности: если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся системе отсчёта
, где при помощи интегрирования, суммируются интервалы времени в локально инерциальных системах отсчёта. 3) Относительность одновременности: если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся системе отсчёта 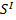 , то они будут неодновременны относительно «неподвижной» системы S. При
, то они будут неодновременны относительно «неподвижной» системы S. При  из преобразований Лоренца следует
из преобразований Лоренца следует 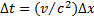 Если
Если 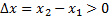 , то и
, то и 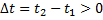 . Это означает, что, с точки зрения неподвижного наблюдателя, левое событие происходит раньше правого
. Это означает, что, с точки зрения неподвижного наблюдателя, левое событие происходит раньше правого 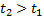 . Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве. Пусть в двух системах отсчёта, вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов они показывают одинаковое время. Первый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают центральные часы. Аналогична ситуация для наблюдателей в S' (второй рисунок).
. Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве. Пусть в двух системах отсчёта, вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов они показывают одинаковое время. Первый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают центральные часы. Аналогична ситуация для наблюдателей в S' (второй рисунок). 

4. сокращение линейных размеров: если длину (форму) движущегося объекта определять при помощи одновременной фиксации координат его поверхности, то из преобразований Лоренца следует, что линейные размеры такого тела относительно «неподвижной» системы отсчёта сокращаются:  , где
, где  — длина вдоль направления движения относительно неподвижной системы отсчёта, а
— длина вдоль направления движения относительно неподвижной системы отсчёта, а 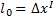 — длина в движущейся системе отсчёта, связанной с телом (собственная длина тела). При этом сокращаются продольные размеры тела (то есть измеряемые вдоль направления движения). Поперечные размеры не изменяются.Такое сокращение размеров ещё называют лоренцевым сокращением. При визуальном наблюдении движущихся тел, дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит повёрнутым, но не сжатым в направлении движения. 5. Длительность событий в разных системах отсчета: длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой это точка неподвижна или часы, движущиеся относительно инерц системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета относительно которой часы движутся: : длительность события в системе
— длина в движущейся системе отсчёта, связанной с телом (собственная длина тела). При этом сокращаются продольные размеры тела (то есть измеряемые вдоль направления движения). Поперечные размеры не изменяются.Такое сокращение размеров ещё называют лоренцевым сокращением. При визуальном наблюдении движущихся тел, дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит повёрнутым, но не сжатым в направлении движения. 5. Длительность событий в разных системах отсчета: длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой это точка неподвижна или часы, движущиеся относительно инерц системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета относительно которой часы движутся: : длительность события в системе  :
: 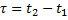 , в системе
, в системе 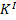 :
: 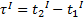 , 1 и 2 – начало и конец события, где
, 1 и 2 – начало и конец события, где 

